
1. Продовжить твердження:
„В усіх формулах еквівалентності під D розуміється будь-який вираз, такий що 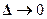 .
.  ,
, 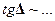 ,
,  ,
, 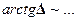 ,
,  ,
,  ,
,  ,
, 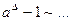 ,
,  ,
,  ,
,  ”
”
2. Функція y=f(x) задана різними аналітичними виразами в різних областях зміни незалежної змінної. Знайти точки розриву, якщо вони існують. 
1) при х=-2 функція неперервна, х=0 – розрив І-го роду.
2) х=-2, х=0 – розриви І-го роду.
3) х=-2 - розрив ІІ-го роду, х=0 – розрив І-го роду.
4) при х=0 функція неперервна, х=-2 – розрив І-го роду
3. Обчислити границі з невизначеністю типу  та
та  :
:
а) 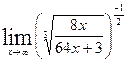 ; б)
; б) 
1. а)  ; б) ; б) 
| 2. а)  ; б) 1 ; б) 1
| 3. а)  ; б) ; б) 
| 4. Інша відповідь |
4. Обчислити границі із застосуванням першої та другої цікавих границь а)  ; б)
; б) 
1.а)  ; б) ; б) 
| 2.а) 16; б) 
| 3.а) 8; б) 
| 4.Інша відповідь |
Тест № 30
1. Продовжить формулювання:
„Послідовність {xn} називається збіжною, якщо..”.
2. Функція y=f(x) задана різними аналітичними виразами в
різних областях зміни незалежної змінної. Знайти точки розриву, якщо вони існують. 
1) х=0, х=2 – розриви І-го роду.
2) при х=2 функція неперервна, х=0 – розрив І-го роду.
3) х=2 - розрив ІІ-го роду, х=0 – розрив І-го роду.
4) при х=0 функція неперервна, х=2 – розрив І-го роду
3. Обчислити границі з невизначеністю типу  та
та  :
:
а) 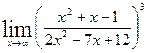 ; б)
; б) 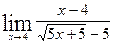
1. а)  ; б) ; б) 
| 2. а)  ; б) ; б) 
| 3. а)  ; б) ; б) 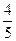
| 4. Інша відповідь |
4.Обчислити границі із застосуванням першої та другої цікавих границь а) 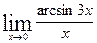 ; б)
; б) 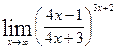
1. а) 3; б) 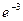
| 2. а) 1; б) 
| 3. а) 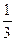 ; б) ; б) 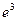
| 4. Інша відповідь |
Контрольні запитання
| Модуль №1. Елементи лінійної алгебри | |
| Що називається детермінантом? | |
| Чим обумовлений порядок визначника? | |
| Як звуться величини, що входять до визначника? | |
| Що означають індекси елементів? | |
| Як позначаються елементи детермінанта? | |
| Що називається детермінантом 2 порядку? | |
| Скільки рядків і скільки стовпців має детермінант 2 порядку? | |
| Що називається детермінантом 3 порядку? | |
| Скільки рядків і скільки стовпців має детермінант 3 порядку? | |
| Як позначають детермінант n-го порядку? | |
| Скільки рядків і скільки стовпців має детермінант n порядку? | |
| Скільки елементів має детермінант 2 порядку? | |
| Скільки елементів має детермінант 3 порядку? | |
| Скільки елементів має детермінант n порядку? | |
| Що називається транспонуванням визначника? | |
| Які властивості транспонування визначників? | |
| Які наслідки властивості транспонування визначників? | |
| Які властивості визначників вам відомі? | |
| Дати означеня мінора елемента. | |
| Дати означеня алгебраічного доповнення елемента. | |
| Чому дорівнює визначник, один з рядків якого складається з нулів? | |
| Чому дорівнює визначник при перестановці його паралельних рядків? | |
| Чому дорівнює визначник, усі елементи якого мають спільний множник? | |
| Чому дорівнює визначник, відповідні елементи двох паралельних рядків якого дорівнюють один одному? | |
| Чому дорівнює визначник, відповідні елементи двох паралельних рядків якого пропорційні один одному? | |
| Чому дорівнює визначник, усі елементи одного з рядків якого являють собою суми двох доданків? | |
| Чому дорівнює визначник, якщо додати до елементів одного з рядків відповідні елементи паралельного рядка, помножені на один і той же множник? | |
| Чому дорівнює визначник, усі елементи будь-якого рядку якого, крім одного, дорівнюють нулю? | |
| Указати правило розкриття визначників 2 порядку. | |
| Перерахувати методи розкриття визначниів 3 порядку. | |
| Вивести формулу розкладання детермінанта по елементам будь-якого рядка. | |
| Чому дорівнює сума добутків елементів будь-якого рядка детермінанта та алгебраічних доповнень відповідних елементів іншого паралельного рядка? | |
| Як обчислити визначники вищих порядків? | |
| Як знизити порядок детермінанта n порядку? | |
| Дати означення матриці. | |
| Як називаються величини, з яких складена матриця? | |
Де розташовані елементи 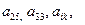 матриці? матриці?
| |
| Чим відрізняються матриці від визначників? | |
| Чи можна матрицю обчислити? | |
| Які види матриць існують? | |
| Які матриці називають прямокутними? | |
| Які матриці називають квадратними? | |
| Які матриці називають діагональними? | |
| Які матриці називають скалярними? | |
| Які матриці називають одиничними? | |
| Які матриці називають нульовими? | |
| Коли 2 матриці вважаються рівними? | |
| Яка матриця називається транспонованою до данної матриці? | |
| Що зветься детермінантом квадратної матриці? | |
| Чи можна говорити про детермінант прямокутної матриці? | |
| Що зветься мінором k-го порядку матриці? | |
| Що зветься рангом матриці? | |
| Як визначають ранг матриці? | |
| Які дії над матрицями існують? | |
| Як помножити матрицю на число? | |
| Як знайти алгебраічну суму двох матриць? | |
| Які матриці можна додавати? | |
| Які матриці можна віднімати? | |
| Як помножити матрицю на матрицю? | |
| Які матриці можна перемножувати? | |
| Чи завжди існує добуток матриць? | |
| Чи має добуток двох матриць переставну властивість? | |
| Яка матриця зветься неособливою? | |
| Яка матриця зветься невиродженою? | |
| Які характерні властивості матриць вам відомі? | |
| Яка матриця має назву оберненої до заданої? | |
| Як позначають обернену матрицю? | |
| Чи завжди існує обернена матриця? | |
| Які матриці мають обернену? | |
| Як знайти обернену матрицю? | |
| Яка матриця зветься приєднаною до данної матриці? | |
| Як виражають обернену матрицю через приєднану? | |
| Як знайти обернену матрицю за допомогою метода Гауса? | |
| Які алгебраічні рівняння мають назву лінійних і чому? | |
| Що зветься системою лінійних алгебраічних рівнянь? | |
| Яке співвідношення між кількістю невідомих та кількістю рівнянь може бути у системі лінійних алгебраічних рівнянь? | |
| Як позначаються коефіцієнти такої системи? | |
У якому рівнянні та який коефіцієнт позначають  ? ?
| |
| Які види систем вам відомі? | |
| Яка система називається однородною? | |
| Яка система називається неоднородною? | |
| Що зветься розв’язком системи? | |
| Яка система називається сумісною? | |
| Яка система називається несумісною? | |
| Яка система називається невизначеною? | |
| Яка система називається визначеною? | |
| Коли однорідна система n лінійних алгебраічних рівнянь з n невідомими має нетривіальний розв’язок? | |
| Як звести систему лінійних алгебраічних рівнянь до одного рівняння? | |
| У чому сутність метода Крамера? | |
| Які системи лінійних алгебраічних рівнянь можна розв’язувати за правилом Крамера? | |
| Чи раціонально системи лінійних алгебраічних рівнянь розв’язувати за правилом Крамера? | |
| Як виявити згідно з правилом Крамера, чи є система сумісною? | |
| Як виявити згідно з правилом Крамера, чи є система не сумісною? | |
| Як виявити згідно з правилом Крамера, чи є система визначеною? | |
| Як виявити згідно з правилом Крамера, чи є система невизначеною? | |
| У чому сутність метода Гауса? | |
| На скільки може зменшитись кількість рівнянь системи після виключення однієї невідомої і чому? | |
| Як визначають несумісність системи у методі Гауса? | |
| Як визначають визначеність системи у методі Гауса? | |
| Як визначають невизначеність системи у методі Гауса? | |
| Як перевірити правильність розв’язання системи? | |
| При якому співвідношенні між кількістю невідомих та кількістю рівнянь системи лінійних алгебраічних рівнянь її можна розв’язати за методом Гауса? | |
| При якому співвідношенні між кількістю невідомих та кількістю рівнянь системи лінійних алгебраічних рівнянь може бути виначеною? | |
| При якому співвідношенні між кількістю невідомих та кількістю рівнянь системи лінійних алгебраічних рівнянь може бути невиначеною? | |
| При якому співвідношенні між кількістю невідомих та кількістю рівнянь системи лінійних алгебраічних рівнянь не може бути виначеною? | |
| У чому полягає метод головних елементів? Які його переваги? | |
| У чому сутність методу оберненої матриці? | |
| Перерахувати переваги та недоліки метода Крамера. | |
| Перерахувати переваги та недоліки метода Гауса. | |
| Перерахувати переваги та недоліки метода оберненої матриці. | |
| Який з методів є більш загальний: метод Гауса чи правило Крамера? Обгрунтуйте. | |
| Як записати систему лінійних рівнянь у матричній формі? | |
| Як записати розв’язок системи у матричній формі? | |
| Чи раціонально знаходити розв’язок системи за допомогою оберненої матриці? |
| Модуль №2. Аналітична геометрія на площині та в просторі. | |
| Що називається вектором? | |
| Як позначають вектори? | |
| Що називається модулем вектора? | |
| Як позначають модуль вектора? | |
| Які вектори вважаються рівними? | |
| Який вектор називається нульовим? | |
| Які вектори називаються колінеарними? | |
| Які дії над векторами вам відомі? | |
| Що називається сумою векторів? | |
| Що називається різницею векторів? | |
| Які вектори називаються взаємно протилежними? | |
| Як позначаються взаємно протилежні вектори? | |
| Що називається добутком вектора на скаляр? | |
| Що називається ортом вектора? | |
| Як позначаються орти векторів? | |
| Які вектори звуться лінійно – залежними? | |
| Які вектори звуться лінійно – незалежними? | |
| Які вектори називаються компланарними? | |
| Що називається векторним базісом? | |
| Що називається ортонормірованим базісом? | |
| Що називається радіус-вектором точки? | |
| Як знайти координати середини відрізку? | |
| Як знайти координати точки, що ділять відрізок в заданому відношенні? | |
| Що називається проекцією вектора на вісь? | |
| Що називається скалярним добутком векторів? | |
| Де застосовується скалярний добуток векторів? | |
| Дати означеня векторного добутка векторів. | |
| Де застосовується векторний добуток векторів? | |
| Яка трійка векторів зветься правою, яка – лівою? | |
| Дати означеня змішаного добутка векторів. | |
| Де застосовується змішаний добуток векторів? | |
| Які системи координат вам відомі? | |
| Які основні задачі аналітичної геометрії вам відомі? | |
| Чим однозначно визначається положення прямої на площині? | |
| Що називається нормальним вектором прямої? | |
| Що називається напрямним вектором прямої? | |
| Які види рівнянь прямої на площині вам відомі? | |
| Які криві 2 порядка існують? | |
| Що називається колом? | |
| Що називається еліпсом? | |
| Що називається гіперболою? | |
| Що називається параболою? | |
| Як знайти кут між прямими на площині? | |
| Як знайти кут між прямимив просторі? | |
| Як знайти кут між прямою та площиною? | |
| Умова паралельності прямих. | |
| Умова перпендикулярності прямих. | |
| Умова паралельності площин. | |
| Умова перпендикулярності площин. | |
| Що ви знаєте про полярну систему координат? | |
| Які поверхні 2 порядка існують? | |
| Що ви знаєте про полярну систему координат? | |
| Які види рівнянь площини в просторі вам відомі? | |
| Як знайти відстань між прямими? | |
| Як знайти відстань між прямою і площиною? | |
| Як знайти відстань між площинами? | |
| Чим однозначно визначається положення прямої в просторі? | |
| Чим однозначно визначається положення площини? | |
| Що називається нормальним вектором площини? | |
| Як пов’язані пряма та площина в просторі? | |
| Модуль №3. Вступ до математичного аналізу. | |
| Дати означення функції. | |
| Що називається аргументом? | |
| Чи може одному значенню аргумента відповідати декілька значень функції? | |
| Чи може різним значенням аргумента відповідати теж саме значення функції? | |
| Що називається областю визначення функції? | |
| Що називається областю зміни функції? | |
| Що означає задати функцію? | |
| Які способи задання функції існують? | |
| Які обмеження є для області визначення функцій? | |
| Що називається графіком функції? | |
| Класифікація функцій. | |
| Які елементарні функції вам відомі? | |
| Які властивості функцій вам відомі? | |
| Що таке множина? | |
| Які дії над множинами існують? | |
| Що називається приростом змінної величини? | |
| Що називається приростом функції? | |
| Що називається числовою послідовністю? | |
| Дати означення границі числової послідовності. | |
| Дати означення границі функції неперервного аргументу. | |
| Які теореми про границі вам відомі? | |
| Які невизначенності існують? | |
| Яка теорема дозволяє позбавитися невизначеностей? | |
| Дати означення неперервності функції в точці. | |
| Як дослідити функцію на неперервність в точці? | |
| Як дослідити функцію на неперервність на відрізку? | |
| Які чудові границі вам відомі? | |
| Що називається першою чудовою границею? | |
| Що називається другою чудовою границею? | |
| Що називається третьою чудовою границею? | |
| Які точки розриву функцій вам відомі? | |
| Чи можна усунути розрив першого роду? | |
| Чи можна усунути розрив другого роду? | |
| Які розриви називаються усувними? | |
| Які розриви називаються ізольованими точками функції? | |
| Що називається нескінчено малою величиною? | |
| Які властивості мають нескінчено малі? | |
| Які нескінчено малі звуться еквівалентними? | |
| Що називається нескінчено великою величиною? | |
| Які властивості мають нескінчено великі? | |
| Які нескінчено малі звуться еквівалентними? | |
| Яка залежність існує між нескінчено малими та нескінчено великими величинами? | |
| Записати таблицю еквівалентних нескінчено малих. | |
| Записати таблицю еквівалентних нескінчено малих. | |
| Які теореми неперервність функцій вам відомі? |
Додаток 1.
Графік організації і контролю самостійної роботи
Дата добавления: 2015-07-25; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тест № 28 | | | Завдання 1. |