Читайте также:
|
Навести конкретні приклади до усих властивостей визначників і довести їх.
1. Доведемо, що: 
= 
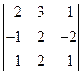, тобто величина визначника не зміниться при заміні всіх його рядків відповідними стовпцями (при транспонуваанні). 
Доведення:
=
= 
=
=
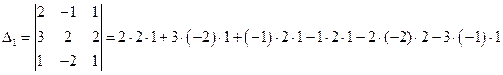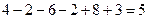
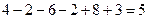
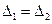, що і треба було довести.
2. Доведемо, що: = -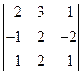 
, тобто при перестановці двох сусідніх рядків або стовпців визначник змінює знак на протилежний.
Доведення:
=
=
= 
= = 
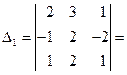
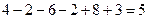
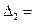
, тобто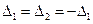 
, що і треба було довести.
3. Доведемо, що: 
= 0, тобто якщо рядки або стовпці визначника пропорційні іншим його рядкам або стовпцям, то визначник дорівнює нулю.
Доведення:
= 
= 
=
= 
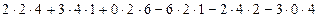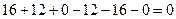, що і треба було довести.
4. Доведемо, що: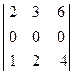 
= 0, тобто визначник, що має нульовий рядок або стовпець, дорівнює нулю.
Доведення: =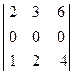 
= 0,
що і треба було довести.
5. Доведемо, що: 
= 
, тобто множник, загальний для елементів рядка або стовпця можна виносити за знак визначника.
Доведення:
= 
= 
.
= = 
=
= 
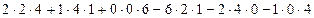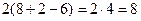, що і треба було довести.
6. Доведемо, що: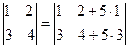 
, тобто величина визначника не
зміниться, якщо до елементів деякого його рядка або стовпця
додати елементи іншого його рядка або стовпця, заздалегідь домножені на один множник.
Доведення:
= 
, 
,
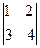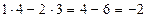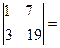
що і треба було довести.
7. Доведемо, що: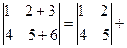 
, тобто, якщо елементи деякого рядка або стовпця визначника представляють собою суму двох величин, то такий визначник можна представити у вигляді суми двох визначників.
Доведення:
= 
, 
= 
=
= 
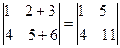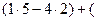
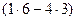, що і треба було довести.
8. Якщо всі елементи визначника, що з одного боку від головної діагоналі дорівнюють 0, то такий визначник дорівнює добутку елементів головної діагоналі: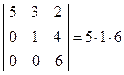 
= 30. Доведення:
= 
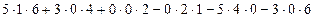= 30.
9. Сума добутків елементи деякого рядка або стовпця визначника на відповідні алгебраічні доповнення елементів іншого рядка або стовпця дорівнює нулю. 
Доведення: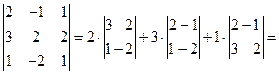 
= 
=
= 
0, оскільки 
;
;
.
Дата добавления: 2015-07-25; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тест № 29 | | | Завдання 3. |