
|
Читайте также: |
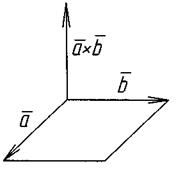
Df Векторний добуток двох векторів – це інший вектор 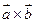 , перпендикулярний площині, що утримує вектори
, перпендикулярний площині, що утримує вектори 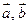 , який задовольняє умовам:
, який задовольняє умовам:
1) Довжина 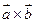 дорівнює добутку довжин векторів
дорівнює добутку довжин векторів  на сінус кута між ними |
на сінус кута між ними | 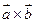 |
|  .
.
2) Вектор векторного добутку 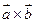 =
= 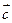
перпендикулярний обом векторам 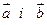 .
.
3) 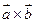 спрямований так, що вектори
спрямований так, що вектори  і
і 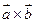 маютьту саму орієнтацію, що і вектори базису.
маютьту саму орієнтацію, що і вектори базису.
Властивості:
1. Порядок множників важливий.
2. 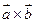

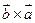
3. 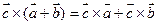
4. 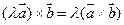 =
= 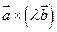
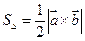
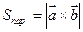
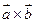 = 0
= 0
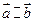 ,
, 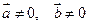 .
Вектор, перпендикулярний до площини, в якій розташовані
.
Вектор, перпендикулярний до площини, в якій розташовані 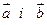 , спрямований в сторону, суміщення одного вектора з другим буде здаватися минаючим проти годинникової стрілки (величина його чисельно дорівнює площі паралелограма на векторах).
, спрямований в сторону, суміщення одного вектора з другим буде здаватися минаючим проти годинникової стрілки (величина його чисельно дорівнює площі паралелограма на векторах).
 ,
, 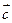 права (ліва),якщо після перенесення їх до спільного початку вектор
права (ліва),якщо після перенесення їх до спільного початку вектор 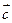 розташовується по той бік від площини, обумовленої векторами
розташовується по той бік від площини, обумовленої векторами  , звідки здається, що найкоротший поворот від
, звідки здається, що найкоротший поворот від 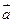 до
до  проти стрілки годинникової (за годинниковою стрілкою).
проти стрілки годинникової (за годинниковою стрілкою).
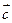
 права
трійка
права
трійка
 ліва
ліва
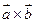 )∙
)∙ 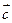
 Результат скалярного множення векторного добутку двох векторів на третій.
Результат скалярного множення векторного добутку двох векторів на третій.  ,
, 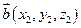 ,
, 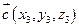 .
(
.
(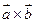 )∙
)∙ 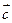 =
= 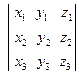 =
= 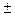
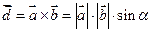 , (
, (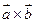 )∙
)∙ 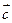 =
= 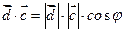 Властивості:
1. Порядок множників важливий:
при круговій перестановці векторів їх добуток незмінний, при перестановці двох множників – змінює знак на протилежний.
2. Умова компланарності:
Властивості:
1. Порядок множників важливий:
при круговій перестановці векторів їх добуток незмінний, при перестановці двох множників – змінює знак на протилежний.
2. Умова компланарності: 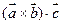 = 0.
= 0.
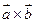 є ортогональним площині векторів
є ортогональним площині векторів  , тобто
, тобто 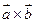

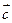 .
3.
.
3. 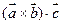 = 0, якщо хоча б один вектор
дорівнює нулю.
4.
= 0, якщо хоча б один вектор
дорівнює нулю.
4. 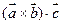 =
=  Праві системи координат –системи, базисні вектори яких утворюють праву трійку.
Праві системи координат –системи, базисні вектори яких утворюють праву трійку.
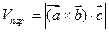
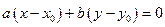 2. а х + bу + с = 0
3.
2. а х + bу + с = 0
3.  4.
4. 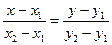 5.
5. 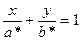 6. у – у0 = k(х – х0)
пучок прямих
М0 – центр пучка
7. у = kх + b
8.
6. у – у0 = k(х – х0)
пучок прямих
М0 – центр пучка
7. у = kх + b
8. 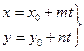 9.
9. 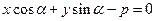 Рівняння лінії в просторі –це рівняння із змінними х, у, z, якому задовольняють координати будь-якої точки цієї лінії і не задовольняють координати точки, що не належить площині.
Вид рівняння
1.
Рівняння лінії в просторі –це рівняння із змінними х, у, z, якому задовольняють координати будь-якої точки цієї лінії і не задовольняють координати точки, що не належить площині.
Вид рівняння
1. 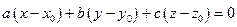 2. а х + bу + сz + d = 0
3.
2. а х + bу + сz + d = 0
3. 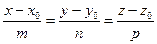 4.
4. 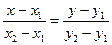 =
= 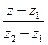 5.
5. 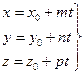 6.
6. 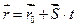 7. а 1 х + b1 у + с1 z + d 1 + +
7. а 1 х + b1 у + с1 z + d 1 + + 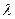 (а 2х + b2у+ с2z + d2)= 0
Вид рівняння
1.
(а 2х + b2у+ с2z + d2)= 0
Вид рівняння
1. 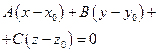 2. А х + Ву + Сz + D = 0
3.
2. А х + Ву + Сz + D = 0
3. 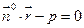 4.
4. 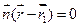
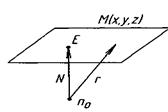 5.
5. 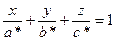 6.
6. 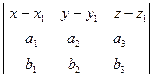 = 0
7.
= 0
7.  = 0
= 0
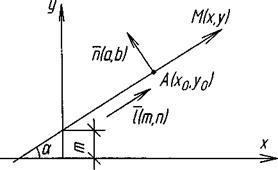 Напрямок задається:
1) Нормальним вектором
Напрямок задається:
1) Нормальним вектором  (а,b), перпендикулярним до прямої;
2) Напрамляючим вектором
(а,b), перпендикулярним до прямої;
2) Напрамляючим вектором  (m,n), паралельним до а.
Назва та позначення
Рівняння прямої, що проходе через точку
(m,n), паралельним до а.
Назва та позначення
Рівняння прямої, що проходе через точку 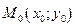 перепендикулярнонормальному вектору
перепендикулярнонормальному вектору  (а,b).
Загальне рівняння прямої,де а,b – координати перпендикуляра
(а,b).
Загальне рівняння прямої,де а,b – координати перпендикуляра  до прямої.
Канонічне рівнянняпрямої.
до прямої.
Канонічне рівнянняпрямої.
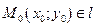 , (m,n)- координати напрямного вектора
, (m,n)- координати напрямного вектора  , який паралельний прямій
, який паралельний прямій 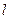 .
Рівняння прямої, що проходе через дві точки
.
Рівняння прямої, що проходе через дві точки 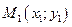 та
та 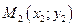 ,
, 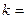
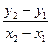 .
Рівняння прямої в відрізках.
На вісі ОХ відрізок а*=
.
Рівняння прямої в відрізках.
На вісі ОХ відрізок а*=  , на вісі ОУ -відрізок b*=
, на вісі ОУ -відрізок b*= 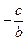 .
Рівняння прямої, що проходе через точку
.
Рівняння прямої, що проходе через точку 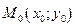 з кутовим коефіцієнтом
з кутовим коефіцієнтом 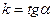 , де α-кут нахилу прямої до осі ОХ.
Рівняння прямої з кутовим коефіцієнтом
, де α-кут нахилу прямої до осі ОХ.
Рівняння прямої з кутовим коефіцієнтом 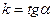 , де b – відрізок, який відтинає пряма на вісі ОУ.
Параметрична форма,де t – параметр,
, де b – відрізок, який відтинає пряма на вісі ОУ.
Параметрична форма,де t – параметр,
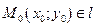 , напрамляючий вектор
, напрамляючий вектор  (m,n).
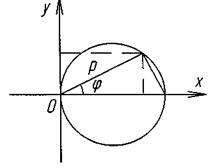
Нормальне рівняня прямої, де
(m,n).
Нормальне рівняня прямої, де 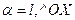 , р – перпендикуляр із О(00) на пряму.
Перехід від (2) до (9):
Необходно (2) домножити на
N =
, р – перпендикуляр із О(00) на пряму.
Перехід від (2) до (9):
Необходно (2) домножити на
N = 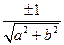 норміруючий множник (знак брати протилежний знаку с).
а,b,с – числа,
норміруючий множник (знак брати протилежний знаку с).
а,b,с – числа, 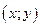 - координати кожної точки прямої.
ПРЯМА В ПРОСТОРІ
Пряма в просторі визначається точкою та напрямком.
Напрямок задається:
1.Нормальним вектором
- координати кожної точки прямої.
ПРЯМА В ПРОСТОРІ
Пряма в просторі визначається точкою та напрямком.
Напрямок задається:
1.Нормальним вектором  (а,b,с), перпендикулярним до площини.
2. Напрамляючим вектором
(а,b,с), перпендикулярним до площини.
2. Напрамляючим вектором  (m,n), паралельним до а.
Найпростіша лінія в просторі – пряма.
Назва та позначення
Рівняння прямої, що проходе через точку
(m,n), паралельним до а.
Найпростіша лінія в просторі – пряма.
Назва та позначення
Рівняння прямої, що проходе через точку 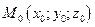 перепендикулярнонормальному вектору
перепендикулярнонормальному вектору  (а,b,с).
Загальне рівняння прямої,де а, b, с – координати перпендикуляра
(а,b,с).
Загальне рівняння прямої,де а, b, с – координати перпендикуляра  до прямої
Канонічне рівнянняпрямої.
до прямої
Канонічне рівнянняпрямої.
 , (m,n,р)- координати напрямного вектора
, (m,n,р)- координати напрямного вектора  , який паралельний прямій
, який паралельний прямій 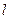 .
Рівняння прямої, що проходе через дві точки
.
Рівняння прямої, що проходе через дві точки 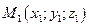 та
та 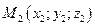 .
Параметрична форма,де t – параметр,
.
Параметрична форма,де t – параметр,
 , напрамляючий вектор
, напрамляючий вектор  (m,n,р).
Векторне рівняня прямої.
(m,n,р).
Векторне рівняня прямої.
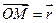 радіуси – вектори точок М і М0 – вектора з початку координат.
радіуси – вектори точок М і М0 – вектора з початку координат.
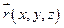 ,
, 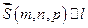 ,
, 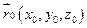 ,
, 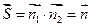
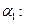
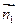
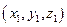 ,
, 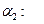

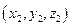 .
Рівняння пучка прямих (через точку перетину двох прямих) з центром в М.
.
Рівняння пучка прямих (через точку перетину двох прямих) з центром в М.
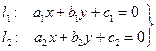
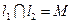 ПЛОЩИНА В ПРОСТОРІ
Площина в просторі визначається точкою та напрямком.
Напрямок задається нормальним вектором
ПЛОЩИНА В ПРОСТОРІ
Площина в просторі визначається точкою та напрямком.
Напрямок задається нормальним вектором  (а,b,с), перпендикулярним до площини.
(а,b,с), перпендикулярним до площини.
 Назва та позначення
Рівняння прямої, що проходе через точку
Назва та позначення
Рівняння прямої, що проходе через точку 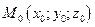 перепендикулярнонормальному вектору
перепендикулярнонормальному вектору  (А,В,С).
Загальне рівняння прямої,де а, b, с – координати перпендикуляра
(А,В,С).
Загальне рівняння прямої,де а, b, с – координати перпендикуляра  до прямої
прямої.
У векторній формі,де р – довжина перпендикуляра із О(0,0,0) на площину α.
до прямої
прямої.
У векторній формі,де р – довжина перпендикуляра із О(0,0,0) на площину α. 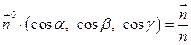 - одиничний вектор, перпендикулярний до площини α.
Через норміруючий множник
- одиничний вектор, перпендикулярний до площини α.
Через норміруючий множник
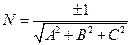 ,
,  (А,В,С)- нормальний вектор площини,
(А,В,С)- нормальний вектор площини, 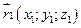 задана М1.
Рівняння прямоїв відрізках.На вісі ОХ відрізок а*=
задана М1.
Рівняння прямоїв відрізках.На вісі ОХ відрізок а*= 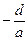 , на вісі ОУ - відрізок b*=
, на вісі ОУ - відрізок b*= 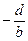 , на вісі ОZ відрізок с* =
, на вісі ОZ відрізок с* = 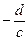 .
Рівняння площини,що проходе через точку
.
Рівняння площини,що проходе через точку 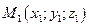 , паралельно двом некомпланарним векторам
, паралельно двом некомпланарним векторам 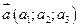 і
і 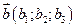 .
Рівняння площини,що проходе через 3 точки
.
Рівняння площини,що проходе через 3 точки 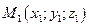 ,
, 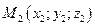 та
та 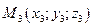 що не належать одній прямій.
що не належать одній прямій.

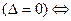
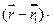
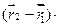
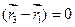
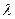 (А2х + В2у+ C2z + D2) = 0
Для кожного
(А2х + В2у+ C2z + D2) = 0
Для кожного 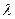 конкретного це рівняння визначає деяку пряму,що проходе через пряму
конкретного це рівняння визначає деяку пряму,що проходе через пряму 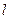 .
Просторова теорема Піфагора:
.
Просторова теорема Піфагора:
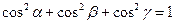 2.
2. 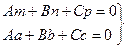 3.
3. 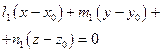 4.
4. 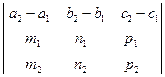 = 0
Ах + Ву + Сz + D = 0
= 0
Ах + Ву + Сz + D = 0
 На площині
Між прямими
На площині
Між прямими 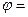
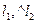 -
між їх нормальними або напрямляючими векторами:
-
між їх нормальними або напрямляючими векторами: 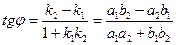


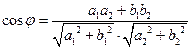 Якщо
Якщо 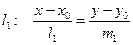
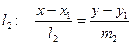 , то
, то
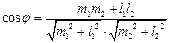
 На площині
Прямі:
На площині
Прямі: 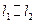 . Якщо
. Якщо
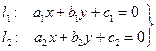
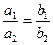 Якщо
Якщо 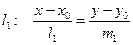
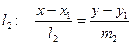
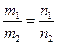 Якщо
Якщо 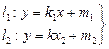
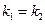
 На площині
Прямі:
На площині
Прямі: 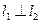 . Якщо
. Якщо
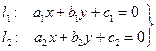 , то
, то 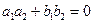 Якщо
Якщо 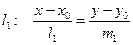
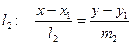
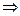
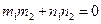 Якщо
Якщо 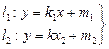 , то
, то 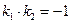
 На площині
Від точки
На площині
Від точки 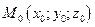 до прямої а х + bу + с = 0
до прямої а х + bу + с = 0
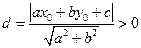 завжди - довжина перпендикуляра із М до прямої.
Відхилення:
завжди - довжина перпендикуляра із М до прямої.
Відхилення: 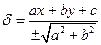
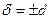 . Норміруючий множник
. Норміруючий множник 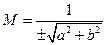 .
. 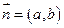 -довжина вектора. Знак протилежний знаку коефіцієнта с в рівнянні прямої.
ГМТ – фігура, яка складається із усих точок площини або простора, що мають властивості певні.
-довжина вектора. Знак протилежний знаку коефіцієнта с в рівнянні прямої.
ГМТ – фігура, яка складається із усих точок площини або простора, що мають властивості певні.
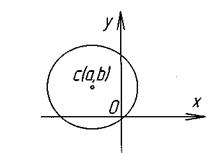

 Коло - частковий випадок еліпса з рівними осями і фокусами в одній точці – центрі кола.
Фокальні радіуси -вектори (
Коло - частковий випадок еліпса з рівними осями і фокусами в одній точці – центрі кола.
Фокальні радіуси -вектори (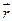 і
і 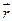 1) точки - відстань точки М(х,у) еліпса від його фокусів:
1) точки - відстань точки М(х,у) еліпса від його фокусів: 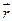 = а -
= а - 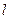 х, r = MF,
х, r = MF,
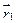 = а +
= а +  х, r1= MF1.
х, r1= MF1.
 1)
1)  або
2)
або
2) 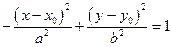 Будуємо прямокутник
Будуємо прямокутник  ,
,  і його
діагоналі - асимптоти, а потім гіперболу, яка перетинає дійсну вісь.
Відстань точки М(х,у) від її фокусів – це фокальні радіус-вектори данної точки.
і його
діагоналі - асимптоти, а потім гіперболу, яка перетинає дійсну вісь.
Відстань точки М(х,у) від її фокусів – це фокальні радіус-вектори данної точки.
 у2 = 2рх - симетрична відносно ОХ.
у2 = 2рх - симетрична відносно ОХ.
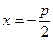 директриса.
х2 = 2qу - симетрична відносно ОУ.
директриса.
х2 = 2qу - симетрична відносно ОУ.
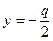 директриса.
Вершина – в початку системи координат фокальний радіус -вектор.
директриса.
Вершина – в початку системи координат фокальний радіус -вектор.

 - рівняння лінії
- рівняння лінії
 - рівняння сфери з центром С
- рівняння сфери з центром С  і радіусом
і радіусом  .
.
 Приклади:
1.
Приклади:
1. 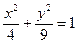 еліптична циліндрична поверхня з твірною паралельною ОZ
2.
еліптична циліндрична поверхня з твірною паралельною ОZ
2. 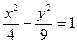 гіперболічна циліндрична поверхня з твірною паралельноюОХ
3.
гіперболічна циліндрична поверхня з твірною паралельноюОХ
3. 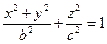 еліпсоід обертання навколо вісі ОZ (обертається еліпс
еліпсоід обертання навколо вісі ОZ (обертається еліпс
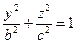 навколо ОZ).
4.
навколо ОZ).
4. 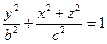 еліпсоід обертання навколо вісі ОУ (обертається еліпс
еліпсоід обертання навколо вісі ОУ (обертається еліпс
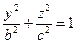 навколо ОУ).
навколо ОУ).
 : А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2= 0
: А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2= 0
 , де
, де
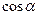 =
=  ,
, 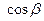 =
= 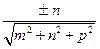 ,
, 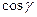 =
=  Пряма належить площині
Пряма належить площині
 : Ах + В у + C z + D = 0,
: Ах + В у + C z + D = 0,
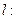
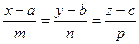 .
Площина утримує точку
.
Площина утримує точку 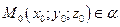
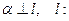
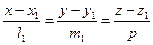 .
Нормальний вектор
.
Нормальний вектор 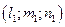 .
Дві прямі належать одній площині
Якщо
.
Дві прямі належать одній площині
Якщо  - зхрещені.
- зхрещені.
 ,
, 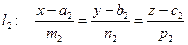 .
.
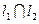 , якщо напрямляючі коефіцієнти не пропорційні і
, якщо напрямляючі коефіцієнти не пропорційні і 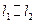 , якщо пропорційні.
Дослідження загального рівняня площини:
1) D = 0 => Ax + By + Cz = 0 – площина проходе через початок координат.
2) A = 0 => By + Cz + D = 0 площина параллельна вісі ОХ.
3) B = 0 => Ax + Cz + D = 0 площина араллельно вісі ОУ.
4) C = 0 => Ax + By + D = 0 площина араллельно вісі OZ.
5)
, якщо пропорційні.
Дослідження загального рівняня площини:
1) D = 0 => Ax + By + Cz = 0 – площина проходе через початок координат.
2) A = 0 => By + Cz + D = 0 площина параллельна вісі ОХ.
3) B = 0 => Ax + Cz + D = 0 площина араллельно вісі ОУ.
4) C = 0 => Ax + By + D = 0 площина араллельно вісі OZ.
5) 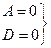 Ву + Cz = 0: у = -
Ву + Cz = 0: у = - 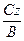 площина обертається навколо вісі OХ.
6)
площина обертається навколо вісі OХ.
6) 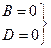 = > Ах + Cz = 0: х = -
= > Ах + Cz = 0: х = - 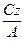 площина обертається навколо вісі ОУ.
7)
площина обертається навколо вісі ОУ.
7) 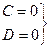 = > Ах + Ву = 0: х = -
= > Ах + Ву = 0: х = - 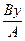 - площина обертається навколо вісі О Z.
8)
- площина обертається навколо вісі О Z.
8) 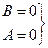 = > Cz + D = 0:
= > Cz + D = 0: 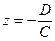 = const площина проходе араллельно площині ХОУ.
9)
= const площина проходе араллельно площині ХОУ.
9) 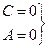 = > Ву + D = 0:
= > Ву + D = 0: 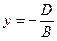 = const площина проходе араллельно площині XOZ.
10)
= const площина проходе араллельно площині XOZ.
10)  = > Ах + D = 0:
= > Ах + D = 0:  = const площина проходе араллельно площині УOZ.
Якщо в рівнянні площини відсутня координата, то площина паралельна цій вісі.
КУТИ
У просторі
Між прямими –між їх нормальними або напрямляючими векторами
= const площина проходе араллельно площині УOZ.
Якщо в рівнянні площини відсутня координата, то площина паралельна цій вісі.
КУТИ
У просторі
Між прямими –між їх нормальними або напрямляючими векторами 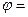
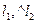
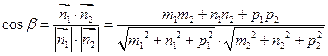
 ,
, 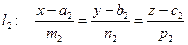 .
Між площинами– між їх нормальними векторами:
.
Між площинами– між їх нормальними векторами:
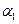 : А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2 = 0
: А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2 = 0
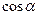 =
= 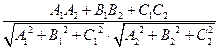 .
.
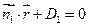 ,
, 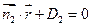
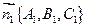 ,
, 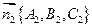 Між прямою та площиною –між прямою і її проекцією на площину.
Між прямою та площиною –між прямою і її проекцією на площину.
 : Ах + В у + C z + D = 0,
: Ах + В у + C z + D = 0,
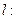
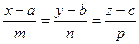 .
.
 УМОВА ПАРАЛЕЛЬНОСТІ
У просторі
Прямих:
УМОВА ПАРАЛЕЛЬНОСТІ
У просторі
Прямих: 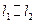 , якщо
, якщо  для
для
 ,
, 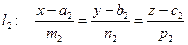 .
Площин:
.
Площин: 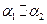 , якщо
, якщо 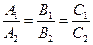
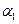 : А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2= 0
Прямої та площини:
: А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2= 0
Прямої та площини: 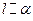 ,
, 
 : Ах + В у + C z + D = 0,
: Ах + В у + C z + D = 0,
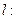
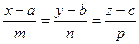 УМОВИ ПЕРПЕНДИКУЛЯРНОСТІ
У просторі
Прямі:
УМОВИ ПЕРПЕНДИКУЛЯРНОСТІ
У просторі
Прямі:
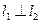 , якщо
, якщо  для
для
 ,
, 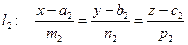 .
Площини:
.
Площини:  , якщо
, якщо 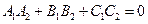 .
.
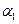 : А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2= 0
Прямої та площини:
: А1 х + В1 у + C1 z + D1 = 0
α2: А2 х + В2у + C2z + D2= 0
Прямої та площини: 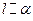 ,
, 
 : Ах + В у + C z + D = 0,
: Ах + В у + C z + D = 0,
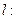
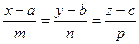 ВІДСТАНЬ
У просторі
Від точки
ВІДСТАНЬ
У просторі
Від точки 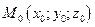 до а х + bу + сz + d = 0 прямої.
до а х + bу + сz + d = 0 прямої. 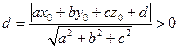 завжди -довжина перпендикуляра із М до прямої.
Від точки
завжди -довжина перпендикуляра із М до прямої.
Від точки 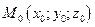 до площини
до площини  :
Ах + В у + C z + D = 0.
:
Ах + В у + C z + D = 0. 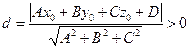 завжди.
Відхилення:
завжди.
Відхилення: 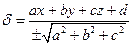 ,
, 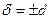 Норміруючий множник
Норміруючий множник 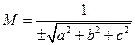
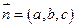 - довжина вектора. Знак протилежний знаку коефіцієнта dв рівнянні прямої.
КРИВІ 2 ПОРЯДКУ
Це лінії, координати точок яких задовольняють рівнянням другого степеня.
Коло
Це геометричне місце точок площини (ГМТ), рівновіддалених від однієї точки – центра.
- довжина вектора. Знак протилежний знаку коефіцієнта dв рівнянні прямої.
КРИВІ 2 ПОРЯДКУ
Це лінії, координати точок яких задовольняють рівнянням другого степеня.
Коло
Це геометричне місце точок площини (ГМТ), рівновіддалених від однієї точки – центра.  С
С 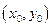 - центр,
- центр,  - радіус.
Коло з центром в початку координат 0(0,0)
- радіус.
Коло з центром в початку координат 0(0,0)
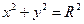 .
Еліпс
Це геометричне місце точок (ГМТ), сума відстаней яких від двох точок F и f1 (фокусів) є величина постійна.
С
.
Еліпс
Це геометричне місце точок (ГМТ), сума відстаней яких від двох точок F и f1 (фокусів) є величина постійна.
С 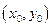 - центр, а, b – піввісі.
а – велика (на ОХ), b – мала(на ОУ).
1) Якщо а > b, то F и f1 на вісі ОХ на відстані с =
- центр, а, b – піввісі.
а – велика (на ОХ), b – мала(на ОУ).
1) Якщо а > b, то F и f1 на вісі ОХ на відстані с = 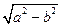 від початку координат.
від початку координат.
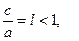
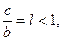 - ексцентриситет.
2) Якщо а < b, то F и f1 на вісі ОУ на відстані с =
- ексцентриситет.
2) Якщо а < b, то F и f1 на вісі ОУ на відстані с = 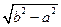 від початку координат.
4) Якщо а = b, то це коло х2 + у2 = а2
Директриси еліпса
від початку координат.
4) Якщо а = b, то це коло х2 + у2 = а2
Директриси еліпса 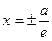 ,
, 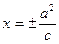 - прямі паралельні малій вісі еліпса, що відстоять від неї на відстані
- прямі паралельні малій вісі еліпса, що відстоять від неї на відстані 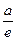 .
Ексцентриситет еліпса
.
Ексцентриситет еліпса 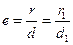 =
= 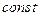 - цевідношення відстаней будь-якої точки еліпса до фокуса і відповідної директриси.
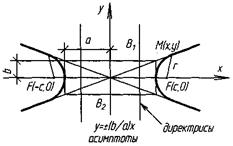
Гіпербола
Це геометричне місце точок площини (ГМТ), різниця відстаней яких від двох даних точок F и f1 (фокусів), є величина постійна: 2а (0 < 2а < FF1). а, b – піввісі.
F(с; о) і f1 (- с; о) - фокуси. | FF1 | = 2с.
1) а – на дійсній піввісі ОХ; х =
- цевідношення відстаней будь-якої точки еліпса до фокуса і відповідної директриси.
Гіпербола
Це геометричне місце точок площини (ГМТ), різниця відстаней яких від двох даних точок F и f1 (фокусів), є величина постійна: 2а (0 < 2а < FF1). а, b – піввісі.
F(с; о) і f1 (- с; о) - фокуси. | FF1 | = 2с.
1) а – на дійсній піввісі ОХ; х = 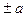 - вершина гіперболи, b – на мнімій піввісі ОУ.
2) b – на дійсній піввісі ОУ; вершина гіперболи у =
- вершина гіперболи, b – на мнімій піввісі ОУ.
2) b – на дійсній піввісі ОУ; вершина гіперболи у = 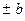 .
а – на мнімій піввісі ОХ. с =
.
а – на мнімій піввісі ОХ. с = 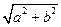 с – відстаньфокуса від початку координат. а – велика (на ОХ), b – мала(на ОУ).
с – відстаньфокуса від початку координат. а – велика (на ОХ), b – мала(на ОУ).
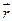 = |- а +
= |- а + 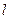 х |,
х |, 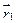 = | а +
= | а + 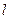 х | - фокальні радіус-вектори асимптоти.
Ексцентриситет гіперболи
х | - фокальні радіус-вектори асимптоти.
Ексцентриситет гіперболи 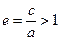 =
= 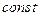 Якщо а = b, то гіпербола рівнобічна
х2 - у2 = а2. Асимптоти: у = х, х = у.
Сполучені:
Якщо а = b, то гіпербола рівнобічна
х2 - у2 = а2. Асимптоти: у = х, х = у.
Сполучені: 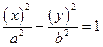 ,
, 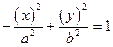 Парабола
Це геометричне місце точок площини,
рівновіддалених від данної точки - фокуса і від данної прямой - директриси.
Парабола
Це геометричне місце точок площини,
рівновіддалених від данної точки - фокуса і від данної прямой - директриси.
 Фокус не належить директрисі.
Фокус не належить директрисі.  Якщо
Якщо 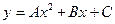 , де
, де 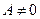 , то це парабола із зміщеною вершиною. Вісь симетрії паралельна ОУ або співпадає з нею.
, то це парабола із зміщеною вершиною. Вісь симетрії паралельна ОУ або співпадає з нею.
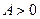 - гілки догори,
- гілки догори, 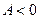 - гілки донизу.
- гілки донизу.
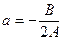 ,
, 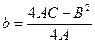 - координати вершини
- координати вершини 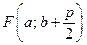 , де
, де 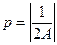 Директриса паралельна ОХ, то у =
Директриса паралельна ОХ, то у = 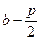 .
Якщо
.
Якщо 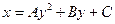 , де
, де 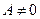 , то це парабола із зміщеною вершиною. Вісь симетрії паралельна ОХ або співпадає з нею.
, то це парабола із зміщеною вершиною. Вісь симетрії паралельна ОХ або співпадає з нею.
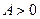 - гілки догори,
- гілки догори, 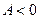 - гілки донизу.
- гілки донизу.
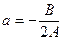 ,
, 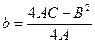 - координати вершини
- координати вершини 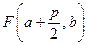 , де
, де 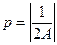 Директриса паралельна ОУ, то х =
Директриса паралельна ОУ, то х = 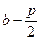 Для визначення геометричного образу, який описує алгебраічне рівняння вигляду
Ах2 + Ву2 + Сх + Dу + F = 0
треба звести його до одного з каноничних
рівнянь ліній другого порядку шляхом виділення повних квадратів:
Для визначення геометричного образу, який описує алгебраічне рівняння вигляду
Ах2 + Ву2 + Сх + Dу + F = 0
треба звести його до одного з каноничних
рівнянь ліній другого порядку шляхом виділення повних квадратів:
 Ві одного знаку – то це рівняння еліпса.
Ві одного знаку – то це рівняння еліпса.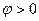 проти годинникової стрілки,
проти годинникової стрілки, 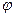 < 0 – за годинниковою стрілкою
< 0 – за годинниковою стрілкою 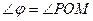 .
Якщо 0
.
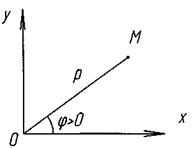
Якщо 0 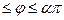 , то кожній точці площини (крім О) відповідає певна пара чисел ρ і φ.
Для полюса ρ = 0, кут φ – будь-який.
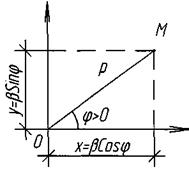
Зв’язок ПОЛЯРНИХ і прямокутних декартових координат.
, то кожній точці площини (крім О) відповідає певна пара чисел ρ і φ.
Для полюса ρ = 0, кут φ – будь-який.
Зв’язок ПОЛЯРНИХ і прямокутних декартових координат.
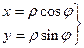
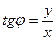 ,
, 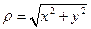 Відстань між точками:
Відстань між точками: 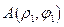 ,
, 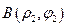
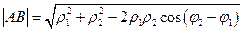 Приклади:
1. ρ = а = Const - к оло з центром в О і
ρ = а, х2+у2 = а2
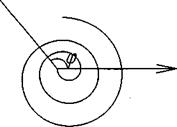
2. ρ = аφ - спіраль Архимеда.
3. ρ = 2acosφ - коло з центром в точці
ρ0 = а, φ = 0, R = a.
Приклади:
1. ρ = а = Const - к оло з центром в О і
ρ = а, х2+у2 = а2
2. ρ = аφ - спіраль Архимеда.
3. ρ = 2acosφ - коло з центром в точці
ρ0 = а, φ = 0, R = a.
 ,
, 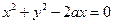 4.
4. 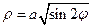 - лемніската
- лемніската 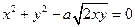 5.ρ = 2acos 3
5.ρ = 2acos 3 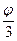 6. ρ = a(1 + cosφ) - кардіоіда
ПОВЕРХНІ 2 ПОРЯДКУ
Це такі поверхні, рівняння яких містять хоча б одну з координат х, у, z у 2 степені.
Конічна –поверхня, яка утворена прямою лінією (твірною), що проходить через задану точку (вершину поверхні) і перетинає задану лінію (напрямну лінію).
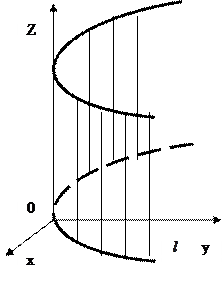
Циліндрична –поверхня, яка утворена прямою лінією (твірною), що проходить паралельно до заданої прямої L (вісі поверхні) і яка проходить через задану лінію
6. ρ = a(1 + cosφ) - кардіоіда
ПОВЕРХНІ 2 ПОРЯДКУ
Це такі поверхні, рівняння яких містять хоча б одну з координат х, у, z у 2 степені.
Конічна –поверхня, яка утворена прямою лінією (твірною), що проходить через задану точку (вершину поверхні) і перетинає задану лінію (напрямну лінію).
Циліндрична –поверхня, яка утворена прямою лінією (твірною), що проходить паралельно до заданої прямої L (вісі поверхні) і яка проходить через задану лінію 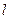 (напрямну лінію).
1.Твірна паралельна ОZ,
(напрямну лінію).
1.Твірна паралельна ОZ, 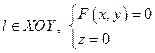 2.
2. 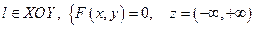 3. Твірна паралельна ОУ,
3. Твірна паралельна ОУ, 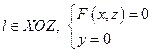 4. Твірна паралельна ОХ,
4. Твірна паралельна ОХ,  Правило знаходження рівняня
проверхні обертання:
1. В рівнянні лінії обертання залишити
незмінною координату, одноіменну з віссю обертання.
2. Другу координату рівняння лінії
обертання замінити на
Правило знаходження рівняня
проверхні обертання:
1. В рівнянні лінії обертання залишити
незмінною координату, одноіменну з віссю обертання.
2. Другу координату рівняння лінії
обертання замінити на 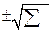 квадратів двох інших просторових координату.
Застосовується метод перерізу.
Застосування кривих та
поверхонь обертання:
1. Будівництво водонапорних башт та
радіощогл (однополостні гіперболоіди).
2. В прожекторах, фарах, антенах
радіолокаторів (параболоіди обертання).
3. Закони Кеплера.
4. Орбіти штучних супутників Землі.
(коло, еліпс, парабола, гіпербола в залежності від швидкості і відстані)…
квадратів двох інших просторових координату.
Застосовується метод перерізу.
Застосування кривих та
поверхонь обертання:
1. Будівництво водонапорних башт та
радіощогл (однополостні гіперболоіди).
2. В прожекторах, фарах, антенах
радіолокаторів (параболоіди обертання).
3. Закони Кеплера.
4. Орбіти штучних супутників Землі.
(коло, еліпс, парабола, гіпербола в залежності від швидкості і відстані)…
Конспект – схема лекції
„Вступ до математичного аналізу”
1. Основні поняття.
2. Множини.
2. Функція однієї змінної.
3. Теорія границь.
5. Неперервність функції.
Дата добавления: 2015-07-25; просмотров: 233 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Розкладання вектора | | | МНОЖИНИ. |