Взаимодействие тел в эфир­ном пространстве обусловливает им равное и про­тивоположное противодействие. 7 страница

т²r = 6,938·10⁶ – const'. (3.71)

Подставляя в (3.71) r = 1,895·10 см, определяем массу m' тела, движущегося с орбитальной скоростью:

m' = 6,05·10² гр.

По силе и массе определяем напряженность g' грави­поля:

g' = 2 F / m' = 1,708·10³ см/с². (3.72)

Результат (3.72) можно получить непосредственно из инвариантной взаимосвязи радиуса шара r и напряжен­ности внешнего гравиполя g:

r²g' = 6,13110⁵ – const'. (3.73)

Подставляя в (3.73) величину радиуса этого уплотне­ния r', имеем:

g' = 1,708·10³ см/с².

Напряженность g' внешнего гравиполя в окрестностях тела изменилась и выросла в 1,71 раза. А это значит, что изменилась пульсация тела, вызывая при движении уп­лотнение своей эфирной шубы. В результате этого уп­лотнения возросла напряженность внешнего гравиполя в окрестностях шара. Именно уплотняющая шуба, кото­рая возникает при любой форме движения, за счет взаимодействия с внешней средой сохраняет изменив­шуюся пульсацию тела относительно постоянной и не позволяет телу сбросить свою деформацию.

Таким образом, расчеты подтверждают диалектиче­ский вывод о том, что движущееся тело качественно отличается от неподвижного, и ни о какой тождест­венности между ними не может быть речи. Любое пере­мещение тела в гравитационном поле есть качествен­ное изменение его состояния, сопровождаемое дефор­мацией, изменением напряженности собственного гравитационного поля и других свойств. С другой сто­роны, взаимодействуя с эфиром, движение тела вызыва­ет деформацию, возрастание и уплотнение шубы, изме­нение внешней напряженности гравитационного поля вокруг тела.

Вывод о том, что физические тела в движении с любой скоростью деформируются при взаимодействии с эфи­ром, может быть подтвержден эмпирически. В печати несколько лет назад появилась информация, что одно из государств строит электромагнитное орудие, способное сообщать снаряду на выходе из ствола скорость до 8·10 км/с при собственной массе снаряда до 100 г (или весом под 100 кг).

Это орудие может быть использовано для проведения эксперимента. Для этого надо сообщить ядру диамет­ром, например, 12-16 см скорость, близкую к орбиталь­ной, и на его пути установить световой экран с фотоэле­ментами или плотную, но проницаемую мишень. Причем мишень должна отстоять от «дула» на некото­ром расстоянии. Если ядро в полете изменяет свой ради­ус, а расчеты показывают, что ядро радиусом 16 см и массой около 80 г при скорости порядка 8 км/с умень­шится в диаметре примерно на 3 см, то экраны зафикси­руют это изменение. По-видимому, уменьшение объема ядра происходит не симметрично, а в направлении дви­жения в большей степени, а в перпендикулярном в меньшей, т.е. ядро принимает форму чечевицы. Поэтому следы в мишенях могут оказаться иными по величине, чем это следует из расчета. Величина уменьшения зави­сит также от свойств материала, из которого изготовле­но ядро.

Можно предложить другой, не менее сложный экспе­римент с использованием вращающегося на орбите кос­мического аппарата. При пролете этого аппарата над оп­ределенной зоной к его орбите запускается ракета с приборами с таким расчетом, чтобы высота подъема ра­кеты оказалась равной высоте орбиты. Сама ракета должна находиться в нескольких сотнях метров в сторо­не от орбиты и точно в тот момент, когда аппарат будет пролетать мимо нее (рис.38).

Рис. 38.

Рас­стояние от ракеты до аппарата должно быть с максимальной точ­ностью зафиксировано как прибо­рами ракеты, так и с Земли. И в самый момент пролета космиче­ского аппарата, когда ракета зави­сает напротив него и почти непод­вижна относительно пространства, ее инструменты фотографируют аппарат по определенной про­грамме. После обработки материа­лов на снимках можно убедиться, что размеры космического аппара­та почти на четверть меньше тех размеров, которые он имел на поверхности Земли (на рис. 38 обозначены штрихами).

По современным представлениям, неравномерное движение тела в пространстве может быть только уско­рением. Само ускорение понимается как скорость изме­нения скорости. Поэтому при движении тела с постоян­ной скоростью его ускорение как бы равняется 0. Однако имеются два особых случая, когда это правило нарушается и ускорение оказывается не связанным с не­равномерным движением тела.

Первый случай — свободное падение отпущенного над поверхностью Земли тела под действием силы притяже­ния. Оно происходит с постоянным ускорением, в точ­ности равным напряженности гравитационного поля Земли, и равенство это объяснения не имеет. Молчаливо допускается, что тождественность ускорения и напря­женности есть случайное совпадение.

Второй случай — появление центростремительного или нормального ускорения при движении тела по окружно­сти с постоянной по модулю скоростью. Возникающее при этом тоже постоянное ускорение а' описывается со­мнительной для думающих физиков формулой:

а' = v²/R,

где v – угловая скорость, R – радиус окружности.

Появление ускорения а' в данном случае оказывается физически непонятным и даже подозрительным, по­скольку оно не исчезает и остается неизменным, пока тело движется по окружности с постоянной скоростью. Подозрительно же оно потому, что по своей размерно­сти и поведению при вращении весьма напоминает на­пряженность гравиполя Земли, тем более что и сила, вы­зываемая ускорением а тела массой т, кажется аналогичной силе притяжения. Физическое объяснение этого явления тоже отсутствует. Подозрительное отно­шение к центростремительному ускорению привело к путанице в понимании физической сути вращения, к за­мене понимания механизма движения хорошо отлажен­ным аппаратом математического формализма.

Поскольку тело при любом движении с ускорением в гравитационном поле деформируется, то эта деформа­ция вызывает изменение количественной величины всех свойств тела, включая на­пряженность его собственного гравитационного поля. Деформация прекращается и сохраняется, когда тело переходит от ускоренного движения к равномерному. Так же сохраняется достигнутая напряженность соб­ственного гравиполя тела. Наблюдаемое нами ускорен­ное движение тела для самого тела является просто изменением величины напряженности собственного гравитаци­онного поля. Переход на движение с постоянной скоро­стью — сохранение достигнутой напряженности своего гравиполя. Замедление движения — раздеформация те­ла, уменьшение напряженности собственного гравипо­ля. Таким образом, понятие «ускорение» и «изменение напряженности гравиполя» есть одно и то же поня­тие. Оно характеризует один и тот же процесс — грави­тационную деформацию тел. Только этот процесс фиксируется внешним наблюдателем как ускорение, а для тела является изменением напряженности собственного гравиполя. Тела, на поверхности Земли, постоянно под­вержены деформации напряженностью внешнего грави­поля. Эта деформация вызывает изменение напряженно­сти гравиполя тел, которое остается в дальнейшем постоянной и обозначается нами как неизменное уско­рение свободного падения. Подъем тела над поверхно­стью Земли приводит к изменению напряженности внешнего гравиполя или, что то же самое, ускорения свободного падения, которое сопровождается строго пропорциональным изменением напряженности грави­поля поднимаемого тела.

Поскольку ускорение есть наблюдаемое извне след­ствие изменения напряженности собственного гра­виполя движущегося тела, то естественно, что при движении с постоянной скоростью, при которой на­пряженность собственного гравиполя остается неиз­менной в течение всего движения, внешний наблюда­тель фиксирует отсутствие ускорения при равно­мерном движении. И делает вывод, что скорость может существовать отдельно от ускорения.

Таким образом, изменение напряженности грави­тационного поля движущегося тела и ускорение его движения есть один и тот же процесс, имеющий два названия. Только первое характеризует статическое со­стояние напряженности тела, а второе — изменение этой напряженности при движении с ускорением. Поэтому возникновение любого ускорения в любом движении есть проявление изменения напряженности гравипо­ля движущегося тела, вызываемое внешними грави­тационными силами.

Изменение напряженности гравиполя движущегося тела связано с еще одним физическим явлением, назван­ным Ньютоном инерцией. Инерция, по его опреде­лению, «...есть способность сопротивления, по кото­рой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состоя­ние покоя или равномерного прямолинейного движения» [2]. Рассмотрим сущность инерции.

Итак, тело, движущееся в пространстве с ускорением, взаимодействует с гравитационным полем, деформирует и изменяет под его воздействием напряженность собст­венного поля и плотность своей шубы. Изменение де­формации, плотности шубы и напряженности самого те­ла не может происходить без приложения определенной силы, без затрат энергии на компенсацию этих процес­сов и, следовательно, без сопротивления силе, движу­щей тело в пространстве с ускорением. Вот это сопро­тивление тела попыткам изменения своего состояния, т.е. попыткам деформировать его, и есть то, что Ньютон называет врожденным свойством тела — инер­цией.

Повторимся. В случае, когда тело внешней силой вы­водится из состояния покоя и разгоняется, деформация тела, возрастание и уплотнение шубы, взаимодействие с эфиром тормозят его движение и фиксируются нами как стремление сохранить состояние своего покоя, т.е. тело проявляет свойство инертности. От­сюда инертность — степень деформации тела, дос­тигнутая в процессе изменения напряженности соб­ственного гравиполя под воздействием извне. Рассмотренный в данном разделе пример с переходом тела радиусом r = 25 см от неподвижного состояния на поверхности к движению по инерции с первой космической скоростью показал, что в результате перехода ра­диус деформируется до величины r' = 18,4 см. Именно деформация, обусловленная воздействием эфира, вызывает сопротивление изменению движения и становится инертностью тела. Сама же деформация, а вместе с ней и асимметрия собственной пульсации тела обеспечивает последующее движение по орбите за счет постепенной раздеформации. Можно по­казать, что аналогичный эффект вызывается опусканием тела в гравитационном поле.

Допустим, что Земля представляет собой сплошной шар и гравиполе вглубь ее изменяется по инварианту R²g – const. Предположим, вслед за Мюпертюи, Вольте­ром, Перельманом, что от полюса до полюса в ней про­рыт сквозной колодец. К одной из стенок его пристрое­на шахта лифта, на котором мы опускаемся с телом до отметки, где радиус тела будет равен r'' = 18,4 см. Если теперь тело бросить в колодец, то оно не будет падать к центру, а зависнет в невесомости в колодце на этом уровне. Если же бросить несколько различных тел, то каждое из них за­виснет на различных уровнях и между ними окажется некоторое нейтральное свободное пространство.

Если их попробовать сдвинуть вместе, они будут от­талкиваться друг от друга. Именно это свойство обу­словливает образование колец вокруг планет (например, у Сатурна).

Определим, на каком расстоянии от центра R' (на ка­кой отметке) радиус тела достигнет 18,4 см. Используя зависимость

r/R = r'/R',

находим:

R' = r'R/r = 4,834·10⁸ см.

По инварианту Rm² = 1,769·10¹⁴ определим, чему рав­на масса тела на отметке R':

R'm² = 1,769·10¹⁴,

т' = 6,05·10² г.

По инварианту R²g = 3,991·10²⁰ находим напряжен­ность гравиполя Земли g' на отметке R':

R²g' = 3,99·10²⁰,

g' = 1,708·10³.

Следовательно, и напряженность внешнего гравиполя g', и масса m' на отметке R' оказываются равными по аб­солютной величине напряженности g и массе т, полу­ченным при переходе тела к движению по инерции с первой космической скоростью. Поскольку тело на от­метке находится в статическом состоянии, то можно ожидать, что вес тела будет обусловливаться силой F' в два раза большей, чем на поверхности Земли. Опреде­лим эту силу:

F' = m'g' = 1,033·10⁶ см/с².

Аналогичную величину F^/ получаем при переходе к орбитальной скорости

F' = F + F' = 1,033·10⁶ см/с².

Однако сила F' не является весом в буквальном по­нимании, поскольку тело на отметке не будет давить на поверхность. Она есть та сила, которая сжимает тело и обеспечивает его невесомость в данном месте. Таким образом, деформация, вызываемая опусканием тела на глубину 1,550·10⁸ см внутрь Земли, и деформация как результат перехода тела к движению по инерции с пер­вой космической скоростью есть следствие одного и того же явления — изменение взаимодействия с напря­женностью внешнего гравиполя. Следовательно, инер­ция и гравитация есть один и тот же физический про­цесс, проявляющийся по-разному при различных формах взаимодействия тел с внешним гравитационным полем.

И снова мы приходим к выводу, что не масса, как это следует по Ньютону, выступает мерой сопротивле­ния изменению движения и инертности тела, а со­противление тела деформации, вызываемой внешним гравитационным полем либо при переносе тела по высоте, либо при его движении в любом направлении.

Если, как полагают по механике Ньютона, с поверхно­сти Земли столкнуть в колодец какое-то тело, то оно, падая к центру с постоянным ускорением, на большой скорости минует его и устремится с замедлением к дру­гому выходу. Достигнув его и на мгновение остановив­шись, оно снова устремится к центру и будет качаться туда и обратно вечно. В покое тело может находиться только в центре Земли.

Русская механика предсказывает, что тело, падая с по­верхности в колодец, сначала движется с ускорением, которое постепенно, под действием нарастающей де­формации, замедляется. И, наконец, когда энергия внут­реннего сопротивления сжатию превзойдет силу воздей­ствия внешнего гравиполя, тело настолько затормозится, что задолго до центра, после некоторого периода коле­баний, зависнет на том уровне, на котором внутреннее сопротивление уравновешивает сжимающее напряжение внешнего гравиполя. Это явление можно назвать инер­ционным зависанием, а уровень зависания — нейтраль­ной зоной гравитационного взаимодействия поля тела и Земли.

Если тело на лифте опустить ниже нейтрального уровня и там отпустить, то оно вместо падения к центру устремится вверх от центра к своей нейтральной зоне. Именно эта картина движения предметов, вызываемая теми же причинами, наблюдается в «таинственной точ­ке» города Санта-Круст (штат Калифорния, США) [25]. Отмечу также, что именно это явление — инерционное зависание тел в гравитационном поле — обусловливает возникновение хвостов у комет при движении их из зо­ны слабой напряженности гравитационного поля в зону сильной напряженности в окрестностях Солнца. Это яв­ление — образование кометных хвостов — может оказать­ся существенным для расчета масс комет в различных областях околосолнечного пространства.

Когда движущееся равномерно тело тормозится внеш­ними силами, происходит процесс раздеформации, свя­занный с рассасыванием эфирной шубы, с выделением накопленной энергии, с изменением условий взаимодей­ствия тела с эфиром. Всякое сопротивление процессу раздеформации сопровождается ускорением раздефор­мации и усилением воздействия тела на предмет, вызы­вающий сопротивление. Если же раздеформация идет со слабым сопротивлением, например вращение ротора в подшипниках, то она может продолжаться до тех пор, пока энергия, накопленная деформированным ротором, полностью не иссякнет, ротор не возвратится к тем па­раметрам, при которых его свойства окажутся сбаланси­рованными со свойствами окружающей среды. Особен­но долог процесс раздеформации тел, запущенных в космос на высокую орбиту. Он протекает годами, деся­тилетиями и долее. Но всегда все искусственные тела обязательно пройдут процесс раздеформации и упадут на те тела, вокруг которых они вращались.

Всякая инертность проявляется деформацией в той области пространства, в которой движется тело и с которой оно взаимодействует. Представление об инер­ции как о движении без взаимодействия, происходящем относительно неподвижной системы отсчета, не со­ответствует реальным процессам природы.

3.7. Вращательное движение тел

в гравитационном поле

Логически замкнутая система постулатов, заложенная в основания механики Ньютона, обеспечивала возмож­ность рассмотрения взаимодействия тел в основном как движения геометрических точек, наделенных свойством массы. Она не допускала выхода за рамки очерченного круга и не способствовала предложению экспериментов, противоречащих постулатам. И только в одном случае запрет нарушался. Таким нарушением было признание инерции особым свойством, способностью тела сопро­тивляться изменению своего положения. А во враща­тельном движении признавались аналоги инерции — центробежные силы, которые возникают как бы из ниче­го и приводят к тому, что тело или часть тела стремится удалиться от оси вращения. В обоих случаях подспудно подразумевалась какая-то форма неясного взаимодейст­вия с какими-то вещественными носителями, обуслов­ливающими как сопротивление изменению своего со­стояния, так и появление растягивающих усилий при вращении.

Однако возникновение центробежной силы, по-видимому, математически найти не удалось. Возможно, такая задача и не ставилась, поскольку не было пред­ставления о физической сущности центробежных сил, а используемый математический аппарат не предлагал способов их получения. Для точки, движущейся по кри­вой, без взаимодействия, математически выводилось два ускорения:

одно — центростремительное — нормальное, направленное по радиусу к оси,

второе — касательное — тангенциальное, которое и становилось источником сил.

Центробежное ускорение нарушало замкнутость систе­мы механических постулатов, выходило за пределы то­чечного представления движения, требовало физическо­го и математического обоснования вызываемых вращением центробежных сил. А таковые обоснования отсутствовали. Более того, их отсутствие легко обосновывалось математически. Приведу стандартный пример такого обоснования сил, появляющихся при движении точки по окружности со скоростью v и соответствую­щим ускорением а в прямоугольной системе координат. Поскольку движется точка, то ускорением для нее явля­ется скорость изменения скорости. При заданном радиу­се-векторе движение геометрической точки относитель­но системы отсчета сводится к исследованию вектора-функции r (t). Для определения движения точки надо за­дать ее положение относительно системы координат в момент времени t, т.е. задать вектор-функцию r (t). Тогда первая производная v (t) = dr (t) /dt является скоро­стью точки, а вторая производная

d (t) = dv (t) /dt = d²r (t)/ dt²,

ее ускорением.

Рис. 39

Если в пространстве X, Y,Z задается траектория дви­жения точки, на которой отмечается начало, направ­ление движения и скалярная функция S (t), длины дуги траектории от начала отсчета до движущейся в момент t точки, то при движении в одном направлении величина функции совпадает с пу­тем, пройденным по траектории (рис.39).

Используем сопровождающий трехгранник из орт τ, п и b касательной, главной нормали и бинормали в точке А траектории (см. рис 39). Поскольку орты есть вектор функции τ = τ (t); п = n (t); b = b (t),то их направление меняется при движении точки А. Определим ориента­цию вектора скорости v (t) и ускорение a(t) относи­тельно осей сопровождающего трехгранника:

v (t) = dr (t) /dt = dr(t)·ds/dS·dt.

Так как dr/dS = τ,

то:

v(t) = τdS/dt, (3.74)

вектор скорости равен по абсолютной величине моду­лю производной ds/dt и направлен по касательной к траектории.

То же для ускорения:

a (t) – dv/dt = d [ dS /(dt) ·τ (t)] /dt = = τd²S/dt² + v²dτ/dS.

Поскольку dτ/ds вектор кривизны, равный п/r и на­правленный по главной нормали (где r – радиус кривиз­ны), то:

a(t) = τd²S/dt² + v²n/r. (3.75)

Следовательно, вектор а соприкасается с плоскостью сопровождающего трехгранника и имеет проекцию на касательное направление:

a_t = d²S/dt² = dv/dt = εr, (3.76)

где ε – угловое ускорение, a_t – касательное (тангенци­альное) ускорение а проекции на направление главной нормали:

а_п = v2/r, (3.77)

оно является нормальным ускорением, всегда направленным к центру кривизны траектории. Следовательно:

а = √ (а_t² + a_n²). (3.78)

Отсюда вытекает, что при движении по окружности касательное ускорение направ­лено перпендикулярно радиу­су окружности, а нормальное — по радиусу к центру. Пол­ное ускорение а постоянно по величине и также направлено внутрь окружности (рис. 40).

Это вполне корректное математическое определение ско-рости, нормального и тан­генциального ускорения может быть подтверждено мно­гими физическими примерами. Так, ускорение свобод­ного падения на поверхности Земли и других небесных Рис. 40. тел направлено по радиусу к центру, планеты и их спут­ники удерживаются силой, составляющей которой, явля­ется ускорение, тоже направленное к центру (?) либо Солнца, либо планет. Вращение тела на тонкой нерас­тяжимой нити имеет в соответствии с механикой уско­рение, направленное к месту крепления нити. Однако это предположение вызывает серьезные сомнения в сво­ей достоверности, а потому рассмотрим некоторые экс­перименты, как бы его подтверждающие.

Процесс возникновения силы F_n, являющейся произ­ведением массы точки т на ускорение а_п:

F_n = ma_n,

получает, согласно механике, объяснение в следующем описании.

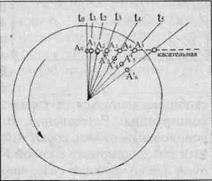
Возьмем расположенный горизонтально диск (рис. 41) и положим на него, в некотором отдалении от центра, шарик А. Начнем раскручивать диск. Поскольку шарик лежит на вращающемся диске, он вместе с диском нач­нет поворачиваться по направле-нию вращения. Однако возни-кающая инерция будет стре-

Рис.41

миться удержать его в том положении, кото­рое он занимал в мо­мент времени t° и обу­словливать ему в процессе вращении сдвиг по касательной к радиусу первоначаль­ного положения. По­этому в каждый после­дующий момент t', t", t'",... положение ша­рика на касательной А', А", А"',... будет все дальше и дальше от­стоять от центра круга. Шарик как бы скользит вдоль радиуса, оставаясь на касательной.

Если теперь шарик закрепить невесомой нитью к цен­тру О и начать вращать диск, то нить будет «притягивать» шарик А°, А°°, А°°°, не давая ему возможности отодвигаться по касательной. Сила F_n, возникающая при натяжении, будет внутренней силой, действующей по направлению нормального ускорения а_п. Перпенди­кулярно ей продолжает действовать тангенциальная си­ла F_t, что соответствует математическому выводу двух ускорений а_п и a_t, представлению о движении тела по инерции и отвергает возможность существования цен­тробежной силы. Именно этим способом объясняется свободное вращение тела на невесомой нити. В книге Роджерса [67] приводится более 20 экспериментов, как бы подтверждающих существование только центрост­ремительной силы, и ни одного, подтверждающего цен­тробежную, поскольку автор их отвергает. Однако такие эксперименты есть. Приведу для примера пару из них:

Рис. 42.

Возьмем цилиндр 1(рис. 42) и с помощью не­весомой нити 2 закрепим один его конец за центр О, а на другом конце поста­вим два пружинных ди­намометра 3один в торец, а другой — со стороны, противоположной на­правлению вращения. Внутри цилиндра поместим шарик 4, способный свободно двигаться от торца к торцу. И раскрутим эту конструкцию. Естественно, что шарик упрется в проти­воположный от оси торец, и будет давить на укреплен­ный там динамометр с силой F. Динамометр и зафикси­рует центробежную силу, направленную от оси. Другой динамометр зафиксирует тангенциальную силу F'. При­чем: F = F'.

Однако можно сказать, что сам торец выполняет роль нити. Объяснение то же, что и для рис. 41. Чтобы дока­зать обратное, заменим трубу кожухом (рис. 43), напо­минающим закрытую тарелку 1. Вместо нити поставим жесткий стержень

Рис. 43

2, дабы исключить болтанку кожуха, что, впрочем, не меняет сути опыта. В кожух поместим шарик 3так, чтобы он мог свободно передвигаться в любом направлении, и динамометр 4. Раскрутим эту конструкцию и обна­ружим, что при некото­рой скорости шарик от кромки тарелки пере­местится к дну О', а ди­намометр зафиксирует центробежную силу, на­правленную от оси и равную F. Но сила, со­ответствующая тангенциальному ускорению F' проявлять себя не будет. Как явствует из рис. 43, шарику для попадания в точку О' придется двигаться навстречу тому движению, которое обеспечивает первая касательная, и занять положение, в котором вторая каса­тельная образует очень малый угол с первой.

Объяснить этот эксперимент существованием только центрост­ремительной силы невозможно. Поэтому подробнее рассмотрим физический механизм враща­тельного движения тел и сопоставим с действием, кото­рое оказывает на неподвижное тело (например, куб) на­пряженность внешнего гравитационного поля (рис. 44).

Рис. 44.

На куб, лежащий на по­верхности Земли, объем­но действует сжимающая сила Р, равная произведе­нию массы тела т на на­пряженность внешнего гравиполя(ускорение свободного падения) Р = mg, фиксируемая как вес.

Точно такая же сила сопротивления Р' действует по всем направлениям от тела: Р = Р'. Однако симметрич­ность по вертикали такого воздействия оставляет тело неподвижным относительно поверхности. А так как на­пряженность гравиполя по высоте h изменяется, то и воздействие ее на куб оказывается асимметричным. В нижней части 1 относительно средней оси РР' это воз­действие сильнее, в верхней 2 — слабее. И вектор напря­женности (ускорения) направлен в ту сторону, в которой напряженность гравиполя больше, т.е. к центру Земли. Следовательно, нормальное ускорение а_n и ускорение свободного падения g для условий Земли является од­ним и тем же параметром. Можно записать:

g = а_п = v²/R. (3.79)

Уравнение (3.79) легко проверить, подставив в него величину первой орбитальной скорости v и радиуса Земли R. Поскольку v = Rω, то, заменив в (3.79) числи­тель значением R²ω², получим:

g = а_п = Rω², (3.80)

g = a_n = vω.. (3.81)

Физический смысл этих формул в том, что всякое ус­корение есть в первую очередь процесс изменения на­пряженности гравиполя, вызванный взаимодействием движущегося тела с вещественным пространством. Изменение напряженности, которое мы фиксируем из­вне и изучаем в виде ускорения, обусловливает все про­цессы взаимодействия, возникает всегда, при любых из­менениях скорости при прямолинейном или криво­линейном движении, но вектор этого ускорения зависит от условий деформации тела.

Дата добавления: 2015-07-11