Третье началоКТД известно как теорема Нернста [77,78], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 1 страница

Таковы основные законы и принципы классической термодинамики, все три начала которой, как показано в [ 77,79 ], оказались логически не связанными друг с другом. Иными словами, в построении классической термодинамики заложен эклектический принцип, ко­торый привел к тому, что она является, по существу, внутренне несогласованной наукой.

Являясь, по общему мнению макрофизической нау­кой, которая не рассматривает микроструктуру вещества и движение микрочастиц в нем, классическая термоди­намика оперирует только независимыми переменны­ми (так называемыми параметрами состояния термоди­намической системы), определяющими вещество ТДС как целое. К параметрам состояния относятся удельная внутренняя энергия, давление, удельный объем, абсо­лютная температура, удельная энтропия, скорость звука и другие. Указанные параметры состояния ТДС могут быть определены экспериментально либо методами ста­тистической физики.

Математический аппарат классической термоди­намики, основанный на свойствах полного дифферен­циала, позволяет описывать изменения параметров со­стояния ТДС только в дифференциальной форме (форме бесконечно малых приращений). Примечательно, что в случае необходимости описания каких-либо процессов в полных параметрах, конечные выражения, содержащие полные параметры (объем, внутреннюю энергию, эн­тропию и т. д.), по форме не отличаются от подобных им выражений, записанных в удельных параметрах, хотя под знаком дифференциала оказывается и масса вещест­ва ТДС.

Тем самым оказывается, что масса приобретает статус параметра состояния ТДС. В этом можно усмотреть противоречие с классической механикой, где масса тела всегда считается постоянной.

Интегрирование дифференциальных соотношений классической термодинамики требует наличия уравне­ния состояния вещества ТДС, которое обычно опреде­ляется опытным путем, либо методами статистической физики. В настоящее время известно более 150 уравне­ний состояний реальных ТДС, которые могут быть све­дены к уравнению состояния реального газа, теоретиче­ски полученному Камерлинг-Оннесом методами статис­тической физики (77,78) в форме:

π = ρv = TαR = Tz, (4.3)

где π – удельная потенциальная энергия ТДС; ρ – дав­ление; v –удельный объем; Т – абсолютная температура: α = f (ρ,T)– безразмерный параметр состояния ТДС, из­вестный как фактор сжимаемости реальною газа; R = 8314/μ дж/кгк газовая постоянная; μ кг/моль – моле­кулярная масса вещества; z = αR.

Следует отметить, как весьма странное то обстоятель­ство, что ни в одном из известных уравнений состоя­ния реальной ТДС не содержится такого параметра состояния, как удельная энтропия S. Параметр же z = αR = f (ρ,T), присутствующий в соотношении (4.3), до сих пор не нашел своего места в математическом аппарате КТД. Это лишний раз свидетельствует о действительно существующей внутренней несогласованности клас­сической термодинамики.

Вместо соотношения (4.3) при проведении операций интегрирования различных соотношений КТД принято пользоваться уравнением состояния идеального газа в форме Клапейрона, которое легко может быть получено из (4.3) при α = 1 и имеет вид [ 77,78 ]:

αv = TR. (4.4)

Модель идеального газа, определяемая соотношением (4.4), настолько прочно утвердилась в современной нау­ке, что фактически является доминирующей в таких важнейших теориях, как газовая динамика, теория тур­булентности, химическая кинетика и др.

Между тем хорошо известно, что в Природе не суще­ствует веществ, обладающих свойствами идеального га­за в достаточно широком диапазоне изменения давления и температуры. Поэтому не удивительно, что интегри­рование точнейших соотношений классической термо­динамики с использованием уравнения (4.4) приводит к приближенным, а часто — и к просто неверным ре­зультатам.

Следует отметить также, что наряду с уравнением со­стояния реального газа в форме (4.3) в классической термодинамике используют и уравнение состояния ре­ального газа в форме Лапласа, которое широко приме­няется для определения квадрата скорости звука в лю­бом однофазном веществе (твердом, жидком, паро- или газообразном) и является, таким образом, универсаль­ным. Обычно это уравнение записывается в виде [ 77,78 ]:

π = w² = γρv = (dp/dρ) _s (4.5)

где π – удельная энергия ТДС в адиабатном волновом процессе; w – скорость звука; γ = с_ρ/c_v = f(ρ,T) – без­размерный параметр ТДС, известный как показатель адиабаты процесса: с_ρ = f(ρ,T), c_v = f(ρ,T) – удельные теплоемкости вещества при ρ = const и v = const', ρ = l/v – плотность вещества.

Как следует из литературы [ 53 ], соотношение (4.5) применяется для определения квадрата скорости звука в твердых телах (если γρ – модуль сдвига или модуль Юнга (для тонких стержней), в жидкостях (если γρ – модуль объемной упругости жидкости), в парах и газах (если; p – давление пара или газа).

С учетом уравнения (4.3) соотношение (4.5) принима­ет вид:

π = w² = γpv = γTαR = γТz = (dp/dρ) _s. (4.6)

Совершенно очевидно из сравнения соотношений (4.5) и (4.6), что (4.6) является более общим, так как содер­жит в себе уравнение (4.3). Поэтому, учитывая универ­сальность равенств (4.5) и (4.6), следует ожидать что уравнение (4.3) может быть использовано не только дня описания состояния реального газа или пара, но и для описания состояния жидких и твердых тел, то есть так­же может оказаться универсальным.

Принципиально важно указать на то, что равенство (4.5) было получено Лапласом в предположении, что распространение звука в веществе представляет со­бой волновой процесс, который происходит без обме­на тепловой энергией между звуковой волной и ок­ружающей средой. Подобные процессы получили в классической термодинамике название адиабатных.

Таким образом, факт наличия в равенствах (4.5), (4.6) или в каких-либо иных соотношениях термодинамики параметра γ следует считать указанием на то, что рас­сматриваемый процесс является физически подобным процессу распространения звука в веществе, т.е. яв­ляется волновым и притом адиабатным.

Однако хорошо известно, что любой волновой про­цесс характеризуется взаимопревращаемостью кинети­ческой и потенциальной энергий. Представив равенство (4.6) в виде [56]:

w² = γpv = ypV/m = γTZ/m,

где V, m – объем и масса вещества термодинамической системы, находим:

mw² = γpV = γТZ.

Отсюда следует ранее неизвестное соотношение:

2Е = γП, (4.7)

идентичное равенству (3.24'), полученному ранее в ме­ханике, где в общем случае Е = mw² /2 + Jω²/2 – кине­тическая, а П = pV= TZ – потенциальная энергия ТДС; J – момент инерции частицы; ω – угловая скорость ее вращения вокруг своей оси. При этом w² = w²_TP + w²_r. Таким образом, очевидно, что параметр

γ = c_p/c_v = 2E/П = f (p,T), (С)

действительно служит количественной мерой взаимо­превращаемости кинетической и потенциальной энергий в волновом адиабатном процессе распростра­нения звука в веществе. Из физики [ 53, 57] известно, что отношение величин этих энергий определяет форму траектории тела (частицы) в пространстве, т.е. в дан­ном случае — форму звуковой волны.

С учетом соотношения (4.7) закон сохранения полной энергии ТДС для волнового адиабатного процесса рас­пространения звука в веществе принимает вид;

W = E ± П = (γ ± 2) П/ 2= (γ ± 2) E/γ = const, (4.8)

где знаки ± учитывают знак потенциальной энергии.

Зависимость γ = f (p,T),присутствующая в равенствах (4.5)÷(4.8), как очевидно, должна представлять собой периодическую функцию, изменяющуюся в простран­стве и во времени. Однако из справочной литературы [80] этого явно не следует. В связи с этим определить истинную форму звуковой волны по справочным дан­ным до сих пор не представлялось возможным.

Являясь наукой, описывающей процессы, происходя­щие (как очевидно) в пространстве и во времени, клас­сическая термодинамика, тем не менее, не оперирует временем как параметром состояния ТДС. Между тем, ввести время в соотношения термодинамики не состав­ляет особого труда. В самом деле, поскольку удельная потенциальная энергия ТДС эквивалентна удельной ра­боте, производимой ТДС над окружающей средой, то с помощью уравнения (4.3) можно записать:

π = l = pv = Tz.

Используя это равенство, можно представить удель­ную работу в виде:

l = lt/t = Nt, (4.9)

где N – удельная мощность; t – время протекания про­цесса. В этом случае равенство (4.1) принимает вид:

du = Tds – pdv = Tds – Ndt. (4.10)

Однако даже такие простейшие временные преобразо­вания, какими являются соотношения (4.9), до сих пор в классической термодинамике не применялись. Возвра­щаясь к равенству (4.1), следует указать, что на его ос­нове, с помощью преобразований Лежандра [77] могут быть получены еще три так называемых характеристи­ческих уравнения классической термодинамики, яв­ляющихся выражениями полных дифференциалов:

удельной свободной энтальпии

dg = –sdT + vdp; (4.11)

удельной энтальпии

di = Tds + vdp; (4.12)

удельной свободной энергии

df = –sdT – pdv. (4.13)

Напомним о том, что преобразования Лежандра по­зволяют установить, является ли данное дифференци­альное соотношение полным дифференциалом функции. Для того чтобы установить это в отношении, например, равенства (4.12), достаточно к обеим частям равенства (4.1) прибавить выражение полного дифференциала d (pv). В результате получим:

du +d (pv)= Tds – pdv + d (pv) = Tds + vdp.

Так как левая часть полученного выражения по свой­ству удельной внутренней энергии (как функции термо­динамических параметров) заведомо является полным дифференциалом, то полным дифференциалом является и его правая часть. Поэтому, обозначая di = du + d (pv), в результате находим, что di = Tds + vdp. Аналогично мо­гут быть получены и проверены соотношения (4.11)–(4.13).

Основываясь на известном из математики [77] необ­ходимом и достаточном условии полного дифференциа­ла (выраженным равенством накрест взятых частных производных), из соотношений (4.1), (4.11), (4.13) нахо­дим следующие дифференциальные соотношения клас­сической термодинамики в частных производных, из­вестные как уравнения Максвелла [77,78]:

(dT/dv) _s = – (dp/ds) _v, (4.14)

(ds/dp) _T = – (dv/dT) _p, (4.15)

(dT/dp)s = (dv/ds) _p, (4.16)

(ds/dv) _T = (dp/dT) _v. (4.17)

Уравнения Максвелла широко используются в класси­ческой термодинамике для определения изменений па­раметров состояния термодинамической системы, по­зволяя сократить количество опытных данных о физических свойствах вещества, обнаружить возможные ошибки, возникающие в экспериментах или расчетах, заменить в уравнениях (при необходимости) одни пара­метры состояния другими.

Столь же важную роль в классической термодинамике играют и удельные теплоемкости [77,78]:

c_p = T (ds/dT) _p, (4.18)

c_v = T (ds/dT) _v. (4.19)

При этом оказывается справедливым равенство:

с_р – c_v = T (dp/dT) _v (dv/dT) _p. (4.20)

Используя, например, уравнение Клапейрона (4.4), с помощью равенства (4.20) можно получить известную формулу Майера для идеального газа:

c_p – c_v = R. (4.21)

Параметры состояния ТДС, которыми только и опери­рует классическая термодинамика, являются среднеста­тистическими (т.е. вероятностными) величинами. По­этому следует ожидать, что известная в КТД статистическая формула Больцмана для энтропии [78]:

S = kln (W), (4.22)

где k – постоянная Больцмана, W – отношение веро­ятностей состояния ТДС) может оказаться не единст­венной в ряду себе подобных. Формула (4.22), которая в классической термодинамике фактически не использу­ется, позволяет осуществлять переход с макро- на микроуровень описания материи и служит, таким обра­зом, своеобразным масштабным соотношением термо­динамической теории.

В начале главы 4 упоминалось, что классическая тер­модинамика способна описывать процессы самой разно­образной физической и химической природы. Действи­тельно, в некоторых работах по классической термодинамике изредка можно встретить уравнения, за­писанные в так называемом обобщенном виде. Напри­мер, в работе [77] дается обобщенная форма записи уравнений Максвелла (4.14)–(4.17). Это достигается тем, что обозначают у ≡ р, а х ≡ v. При этом у играет роль обобщенного потенциала, а х ≡ – обобщенной коор­динаты.

Но если быть последовательным до конца, то необхо­димо признать, что в таком случае любые соотношения классической термодинамики могут быть представлены в обобщенном виде. Фактически это означает, что лю­бые соотношения КТД могут быть использованы для описания не только тепловых, но и механических, электромагнитных и гравитационных взаимодейст­вий.

К сожалению, автору до сих пор не приходилось встречать применения таких параметров, как энтропия и абсолютная температура ни в механике, ни в оптике, ни в электродинамике, ни в каких-либо других не тер­модинамических теориях. Изложенное подводит к вы­воду о том, что классическая термодинамика, являясь по существу универсальной теорией природных взаимо­действий, используется не в полную силу, по-видимому, вследствие ряда спорных и противоречивых обстоя­тельств, часть из которых отмечена в ходе данного ана­лиза. Принципиально важным из них является проблема универсального уравнения состояния ТДС. Именно поэтому указанная проблема должна быть исследована особо.

4.2. Универсальное уравнение состояния

вещества термодинамической системы

Отсутствие в классической термодинамике универ­сального уравнения состояния — ТДС вовсе не означа­ет, что такого уравнения не существует. Результаты не­которых [81] новейших исследований (не выходящих, однако, за рамки привычных представлений КТД) ука­зывают на то, что вероятность существования универ­сального уравнения состояния ТДС чрезвычайно вы­сока. Попытаемся отыскать это уравнение. Для этого запишем уравнение состояния реального газа (4.3) в ви­де [82]:

π = pv = Tz, (4.23)

где π – удельная потенциальная энергия реального газа. Из соотношения (4.23) следует, что в общем виде

π = f₁ (p,v) = f₂ (Tz). (4.24)

Дифференцируя все части этого соотношения, нахо­дим:

dπ = (dπ/dp) _v dp + (dπ/dv) _p dv = (dπ/dT)_zdT + (dπ/dz)_Тdz. (4.25)

С другой стороны, дифференцируя все части равенст­ва (4.23), получаем:

dπ = d(pv)= d(Tz) (4.26)

или

dπ = vdp + pdv = zdT + Tdz. (4.26a)

Сравнивая равенства (4.25) с (4.26а), находим коэф­фициенты:

v = (dπ/dp) _v; p = (dπ/dv) _p;

z = (dπ/dT) _z; T = (dπ/dz) _Т. (4.27)

Представим равенство (4.26а) в виде:

Tdz – pdv = –zdT + vdp. (4.28)

Важно определить, являются ли обе части этого выра­жения полными дифференциалами? Для этого восполь­зуемся преобразованиями Лежандра. Прибавляя к обеим частям (4.28) полные дифференциалы, выраженные ра­венством (4.26), находим тождество:

Tdz + vdp = Tdz + vdp. (4.29)

Применяя теперь к тождеству (4.29) необходимое и достаточное условие полного дифференциала, получаем:

(dT/dp) _z = (dv/dz) _p. (4.30)

С учетом равенств (4.27) для коэффициентов Т и v из (4.30) находим:

d/dp_z ∙ (dπ/dz) _Т = d/dz_p∙(dπ/dp)_γ,

откуда, заменяя индексы Т → р, v → z, получаем:

d²π/dpdz = d²π/dzdp.

Полученное выражение является известным матема­тическим равенством. Поэтому можно заключить, что выражение (4.29), а следовательно и обе части выраже­ния (4.28) являются полными дифференциалами. При­меняя необходимое и достаточное условие полного дифференциала к обеим частям равенства (4.28), полу­чаем:

(dT/dv) _z = – (dp/dz) _v, (4.31)

(dz/dp) _T = – (dv/dT) _p, (4.32)

Сравнивая уравнение (4.32) с уравнением Максвелла (4.15), находим [83]:

(ds/dp) _Т = (dz/dp) _Т = – (dv/dT) _p.

Отсюда получаем:

(ds/dz) _Т = ds/dz = 1.

Это означает, что dz – ds в процессе Т = const. Приме­няя вновь к соотношению (4.26а) преобразования Ле­жандра, вычитая из обеих его частей полные дифферен­циалы d (Tz) = d (pv), получаем тождество:

– zdT – pdv ≡ –zdT – pdv. (4.33)

Применяя к этому тождеству необходимое и доста­точное условие полного дифференциала, получаем:

(dz/dv) _T = (dp/dT) v. (4.34)

С учетом равенств (4.27) для z и р из равенства (4.34) получаем (заменяя индексы z → v, p → Т):

d/dv_Т (dπ/dT) _v = d/dT_v∙ (dπ/dv) _Т,

или

d²π/dvdT = d²π/dTdv.

Тем самым доказано, что выражение (4.33) также яв­ляется полным дифференциалом.

Таким образом установлено, что все исследованные выражения (4.28), (4.29) и (4.33) являются полными дифференциалами. Необходимо, однако, доказать, что dz = ds не только в процессе Т = const, но и в процессах р = const и v = const.

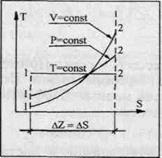
Проще и нагляднее всего это можно сделать, если изо­бразить процесс Т = const в диаграмме T-S (рис. 56). То­гда расстояние между двумя точками 1, 2 на кривой Т = const дает равенство ∆z = ∆s. Если теперь через любую из точек, расположенных на кривой Т = const, провести кривые р = const и v = const, то для соответствующих точек 1, 2 на этих кривых также окажется, что ∆z = ∆s. Переходя к бесконечно малым, получим dz = ds.

Тот же результат можно получить, если сравнить пол­ные дифференциалы:

du = Тds – pdv, (4.1)

di = Тds + vdp, (4.12)

du' = Тdz – pdv, (4.28)

di' = Тdz + vdp, (4.29)

где du', di' – просто обозначения полных дифференциалов (4.28), (4.29).

Из выражений (4.1), (4.28) для процесса v = const находим:

(du/ds) _v = (du'/dz) _v = Т.

Отсюда следует:

du/ds = du'/dz.

Подставляя в числители этого выражения соотношение (4.1), (4.28), получаем dz = ds.

Рис. 56.

Аналогичным образом с помощью равенств (4.12), (4.29) можно показать, что в процессе р = const также dz = ds. Это свидетельствует о том, что dz = ds в любых тер­модинамических процес-сах. Поэтому, интегрируя ра­венство dz = ds в пределах 1 - 2 состояния ТДС, в каких-либо процессах (Т = const, p = const или v = const), на­ходим с учетом обозначения z = Rα (где R – const):

z₂ – z₁ = s₂ – s₁ = R(α₁ – α₂). (4.35)

В графическом изображении (рис. 57) равенство (4.35) представляет собой уравнение прямых, проходящих в координатах z – α и s – α через начала координат и точки 1 и 2 под одинаковыми углами наклона φ = arctg(R) = const этих прямых к осям α. Общий вид урав­нений этих прямых есть z = s = Rα.

С получением равенства z = S = Rα и с учетом уравне­ния (4.31), уравнение (4.23) принимает вид:

π = pv = Ts = Nt. (4.36)

Равенство (4.36) содержит пространственную (v)и временную (t)характеристики ТДС. В связи с этим изла­гаемая далее термодинамическая теория учитывает пространственно-временную сущность любых природных взаимодействий.

Рис. 57

Прежде чем будет оп­ределена действитель­ная роль уравнения (4.36) в термодинамике, проведем дополнтельную провер­ку, смысл которой за­ключается в том, что если это уравнение не противоречит классической термодинамике, то с его помощью могут быть получены любые из извест­ных в КТД соотношений. Для примера с помощью урав­нения (4.36) выведем равенство (4.20):

c_p – c_v = T (dp/dT)_v∙(dv/dT)_p. (a)

Дифференцируя первые три части уравнения (4.36), получаем:

dπ = pdv + vdp = Tds + sdT. (b)

Дифференцируя все части уравнения (b) по Т, сначала при р = const, а затем при v = const, и вычитая почленно полученные результаты, с учетом равенств (4.18) и (4.19) находим

(dπ/dT) _p – (dπ/dT) _v = p (dv/dT) _p – v (dp/dT) _v = T [(ds/dT) _p – (ds/dT) _v ] = c_p – c_v. (c)

Применяя к выражению в квадратных скобках равен­ства (с) известную формулу математики [54]:

(dz/dx) _u = (dz/dx) _y + (dz/dy) _x∙ (dy/dx) _u

и полагая в ней z ≡ s, x ≡ Т, и ≡ р и у ≡ v, получаем:

(ds/dT) _p – (ds/dT) _v = (ds/dv) _T (dv/dT) _p. (d)

Заменяя в выражении (d) с помощью уравнения Мак­свелла (4.17)

(ds/dv)_Т = (dp/dT)_v

и подставляя полученный результат в соотношение (с), получаем формулу (а).

Используя теперь равенство (а), получим формулу Майера (4.21):

c_p – c_v= R (е)

Полагая s = const в уравнении рv = Ts, находим производные (dp/dT)_v = s/v; (dv/dT)_p = s/p, подставляя которые в равенство (а), получаем

(с_р — c_v)_s = Ts/v∙s/p = s = αR.

Отсюда при α = 1 следует формула Майера (е) для идеального газа.

Итак, проверка показала, что уравнение pv = Ts не противоречит классической термодинамике. Более де­тальные исследования также подтверждают этот вывод. Следовательно, уравнение (4.36) может теперь на закон­ных основаниях использоваться в дальнейших выклад­ках.

Прежде всего, определим роль параметра s = αR = f(p,T) в этом уравнении. Поскольку газовая постоянная R = 8314/ µ, [ Дж/кг∙К° ], где µ [ кг/моль ]— молекулярная масса вещества, то удельная энтропия

s = αR = α∙ 8314 /µ =f(p,T), [ Дж/кг∙К° ]

есть параметр состояния ТДС, который устанавливает взаимосвязь между физическими (α = f (p,T)) и хими­ческими (µ) свойствами вещества термодинамической системы. В этом заключается одно из важнейших назна­чений удельной энтропии в термодинамике, чем и объ­ясняется столь успешное ее применение в физической химии. С другой стороны, удельная энтропия соответст­вует удельной работе, производимой термодинамиче­ской системой над окружающей средой (либо окру­жающей средой над термодинамической системой) при изменении температуры на один градус, чем объясняет­ся успешное применение термодинамики и в нехимиче­ских дисциплинах.

При анализе равенств (4.3), (4.5) и (4.6) было высказа­но предположение о том, что уравнение (4.3) может ока­заться одинаково пригодным для описания состояния твердых, жидких, паро- или газообразных ТДС, то есть может оказаться в этом смысле универсальным.

Чтобы убедиться в этом проведем оценку величины параметра α = f(p,T), присутствующего в указанных ра­венствах для подобных веществ. Из равенства (6) нахо­дим: ???

α = w²/γRT = w²µ/γ∙ 8314 Т.

Используя данные работы [ 78 ], расчетом по этой фор­муле находим:

• для стали: (Т = 293 К^о; γ = 1; µ = 56 кг/моль; w = 5130 м/с), α = 605;

• для воды: (Т= 293 K°, γ = 1; µ = 18 кг/моль; w= 1505 м/с), α = 16,74;

Дата добавления: 2015-07-11