Третье началоКТД известно как теорема Нернста [77,78], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 4 страница

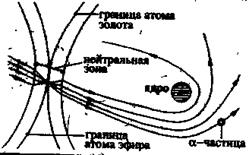
Естественно, что представление о траектории a -час­тиц и их взаимодействиях изменится, если исходить из того, что a -частицы пульсируют и движутся, причем каждая со своей частотой и скоростью в пространстве эфирных молекул по синусоидальной траектории, оги­бая их ядра-сгущения и попадая в более плотную среду молекул твердого вещества (например, золота), изме­няют траекторию своего движения (рис. 59) иначе, чем это показано на рис. 58. На рис. 59 отображается траек­тория движения активных a -частиц в пределах молеку­лы допустим, золота (напомню еще раз, что движение элементарных частиц в любом пространстве, включая эфирное, вне молекул или атомов, невозможно).

Рис.59.

Прежде всего от­мечу, что все моле­кулы золота, как и любого другого ве­щества имеют различные размеры и неодина-ковую плот­ность по всей той об­ласти, которую они образуют. Пульсация этих молекул от ядра, размеры и плот­ность тела ядра тоже различны и только плотность в пределах нейтральной зоны для всех молекул одного вещества примерно одинаковая. Именно эта плотность обусловливает, все свойства вещества.

Траектория a -частиц внутри молекулы определяется индивидуальными свойствами каждой частицы и той скоростью, которую обеспечивают в эфире ее энергетические возможности (самопульсация). Поэтому a-ч астицы проходят через область молекул на различном расстоянии от ядра, и, естественно, что при этом движении происходит постоянное количественное измене­ние свойств частицы, включая ее плотность. Вот эти взаимодействия (так же, как и в классической механике) определяют угол отклонения (рассеивание) их ядром от направления своего движения. Чем ближе подходит a- частица к ядру, тем сильнее отклонение ее траектории.

Угол отклонения (рассеивания) a -частиц в кулоновском поле ядра определяется по формуле Резерфорда:

b = kctgj/ 2, (5.4¢)

где k = ZeE/Mc², Z – заряд ядра, е – заряд частицы, Е – напряженность кулоновского поля ядра, М – масса ядра, с – скорость света, j – угол отклонения частицы.

Формула (5.4') указывает только на то, что a-частицы, пролетая около ядра, отклоняются его кулоновским полем. Из нее не следует, что это откло­ нение является отталкиванием. Одинаково вероятны и отталкивание и притяжение. Но в природе реализует­ся только одно действие — либо отталкивание, либо притяжение. Резерфорд, ориентируясь на то, что заряды ядра и a -частицы положительны, выбрал отталкивание, отскок. И ошибся. Отклонение это не носит харак­тера отскока, а является движением по гиперболи­ческой или параболической траектории как к ядру так и вокруг него. П римерно таким же, как и траектория комет «проры­вающихся» к Солнцу из очень отдаленных глубин кос­моса.

На рис. 59 изображена граница атома эфира и моле­кула золота с ядром, траектория движения a -частиц в молекуле золота. Траектория движения частиц в молекуле и механизм их рассеивания отличаются от предпо­лагаемых (рис.58), но наблюдаемые структуры рассеи­вания частиц вне молекул будут аналогичными. То есть на сегодня нет способов эмпирически отличить траектории друг от друга. Другое отличие заключается в том, что a - частицы, как и электроны, не несут никакого заряда и двигаются не по инерции, а за счет взаимо­действия с электромагнитным (пульсирующим) полем сначала молекул эфира, а затем молекулярного про­странства золота, которое деформирует каждую частицу в зависимости от количественной величины ее свойств. Именно расстояние от ядра и процесс дефор­мации a-частицы на входе в молекулу и раздеформации на выходе обусловливают величину угла отклонения частицы от направления первоначального движения.

Таким образом физический процесс рассеивания a-частиц на атомах не является подобием процесса отскакивания снарядов от стенки, как это было интер­претировано Резерфордом, а есть следствие взаимо­действия движущихся элементарных частиц с изме­няемым пространством тех тел, в которых они двигаются. Эта как бы незначительная и естественная ошибка Резерфорда и послужила отправным пунктом последующего построения математического аппарата квантовой механики. Именно она оказалась прообразом рассуждении о падении электронов на ядро и мысли­мых экспериментов с пулями-электронами, например, «пулемета» Фейнмана, уводивших физиков все дальше и дальше от понимания природы микромира. Надо от­метить также, что дополнительную лепту в некоррект­ное понимание процессов микромира внесло и постули­рование постоянства скорости света, и «изгнание» эфира из физических представлений, и провозглашение неизменности массы и заряда электрона, и... некоторые другие факторы вошедшие в физику еще до начала раз­работки квантовой механики. О них будет сказано да­лее.

5.3. «Квантовые истины»

Итак, эксперименты Резерфорда могут быть объясне­ны иначе, чем это объяснял сам Резерфорд. И кажется, что отличие в объяснениях незначительно. И в том и в другом случае имеет место рассеяние, и в том и в дру­гом случае ядра двигаются в пространстве к ядру и от­клоняются от траектории движения на один и тот же угол в полном соответствии с предсказаниями теории (формула Резерфорда). И все же появилось первое не­понимание природы движения элементарных частиц в атоме, заключающееся в том, что a-частицы движущиеся в атомах эфира и молекулах тел не отскакива­ют от ядра, а огибают его по орбите (как и электро­ны) и вылетают наружу почти под тем же углом, под которым влетали в пространство атома. Исходя из ошибочного объяснения движения элементарных час­тиц в пространстве все больше и больше особенностей механики элементарных частиц понималось в противо­речии с их физической сущностью. Немалую роль в этом процессе сыграло и постулирование отсутствия эфирного пространства, провозглашенного пустотой, и перенесение инерциального движения классической механики на движение элементарных частиц в микро- мире. Именно инерциальное движение электронов по орбите вокруг ядра без излучения энергии противоречило законам электродинамики. Именно оно «застави­ло» Бора, сохраняя планетарную модель Резерфорда, сделать второй ошибочный шаг и сформули-ровать знаменитые постулаты, которые повернули объясне- ние явлений микромира на путь вероятностного толкования, на путь, обусловивший в итоге резкое отличие формулируемых законов микромира от законов класси­ческой механики, что превратило микромир в хаос ве­роятностных взаимодействий. Так в науку начало входить множество необычных квантовых явлений, которые можно назвать «кванто­выми истинами». Истины эти для современных ученых непоколебимы и потому — вечны. Попробую показать, что для объяснения этих явлений нет необходимости в применении «квантовых законов», все они, намного проще и нагляднее, описываются законами классиче­ской механики. Приведу постулаты, введенные Н. Бо-ром в 1913 году, которые запрещали электрону излучение при движении по определенным орбитам в планетарной модели атома. Эти постулаты, являясь второй ошибкой в объяснении природы микромира, и открывают счет квантовым истинам. Вот как обосновывал Н. Бop необходимость в данных постулатах [ 92 ]: «.... мы приходим к выводу, что эти конфигурации со­ответствуют состояниям системы, в которой нет излучения энергии, а потому они будут стационарными, по­ка система не будет возмущена извне».

Позже в работе «О квантовой теории излучения и структуре атома» Н. Бор так обобщил свои предполо­жения [ 92 ]:

«А. Атомная система обладает состояниями, в ко­торых не происходит излучения, связанного с потерями энергии, даже если частицы движутся относительно друг друга и, согласно обычной электродинамике, излу­чение должно иметь место. Такие состояния называют­ся «стационарными» («разрешенными» — А.Ч.) состоя­ниями рассматриваемой системы.

B. Любое испускание или поглощение энергии будет

C. соответствовать переходу между двумя стационар­ными состояниями. Излучение при таком переходе об­ладает определенной частотой, которая определяется соотношением

hv = A — A'

где h – постоянная Планка; А, А' – значение энергии системы в двух стационарных состояниях.

D. Динамическое равновесие систем в стационарном состоянии

E. определяется законами обычной механики, в то время как для перехода из одного состояния в другое эти законы не справедливы (позже было показано, что «справедливы» квантовые законы. – А. Ч.).

D. Различные возможные состояния системы состоя­щей из

E. электрона, движущегося вокруг положительно заряженного ядра, определяются соотношением:

Т= l/2nhw,

где Т – среднее значение кинетической энергии систе­мы, w – частота обращения электрона, n – целое чис­ло».

Вот та первоначальная система постулатов, кото­рая полностью противоречила классической механике, диалектике и даже логике взаимодействий, но оказа­лась приемлемой для научной общественности. Она была заложена в основание новой науки — квантовой механики и, в общем, сохранила свое значение до на­стоящего времени. В дальнейшем я постараюсь показать, что эти постулаты некорректны и не имеют отно­шения к описанию движения элементарных частиц в атоме. Здесь же отмечу что:

A. Стационарное состояние электрона в атоме

B. не­возможно, всякое движение электрона, как и любой макро или микрочастицы, в вещественном простран­стве есть движение с испусканием и поглощением энергии.

B. Испускание энергии при движении электрона происходит постоянно, но только отделение части элек­трона (излучение фотона), изменяющее его массу и за­ряд, влечет изменение частоты электрона и обусловливает переход его на другую орбиту.

С. Все динамические состояния системы атомов и электронов определяются законами классической меха­ники. Специальные, квантовые законы в природе от­сутствуют.

D. Электрон может находиться в атоме на орбите, определяемой его энергетическими возможностями. Движется он по классической траектории и квантовое число п, как и другие предполагаемые квантовые номе­ра, не определяют его орбиты и другие параметры, по­скольку, как и в планетарной системе, орбиты не нуме­руются.

К тому же, как выяснилось впоследствии, целочисленность квантовых номеров оказалась недостаточной для описания состояния электрона в атомах и пришлось вводить новое квантовое число l, определяющее «сплющенность» орбиты, «придающее» n -му номеру соответствующие дополнительные эллиптические ор­биты. Похоже на то, что квантовое число l как раз и за­теняет существование промежуточных (расположенных между целыми п) орбит.

Предположение о волновой природе электронов, вы­сказанное в 1924 году в гипотезе Де Бройля как предпо­ложение о том, что электроны наряду с корпускуляр­ными обладают и волновыми свойствами, соответ­ствовало природе всех тел. Из него следовал вывод о том, что электроны, как и все тела в природе, постоян­но пульсируют. Но такой вывод был слишком революционен и в то время сделан быть не мог, не хватало эм­пирического материала. В результате пришли к соломоновому решению — постулировать электронам, как и всем остальным элементарным частицам, двойствен­ность, обоснованную впоследствии теоретически прин­ципом дополнительности: с одной стороны, они явля­ются частицами не зависящими от волн, а с другой, волнами, не зависящими от частиц. Так в квантовую механику вошел кентавр, отсутствующий в природе — дуализм волна-частица, волница по Р. Фейнману [ 74]. И пришлось впоследствии тому же Де Бройлю почти оправдывать появление этого несуразного образования [ 94]:

«Хочешь не хочешь, — пишет он, — а для полного описания свойств излучения нужно было применять по­очередно картину то волн, то частиц. С другой стороны, соотношение Эйнштейна между частотой и энергией, введенное им на основе его теории фотонов, ясно пока­зывало, что этот дуализм излучения неразрывно связан с самим существованием квантов. Тогда возникает во­прос: не связан ли этот странный дуализм волн и час­тиц, примером которого так замечательно и несомненно явился свет, с глубокой и скрытой природой кванта действия? Не следует ли ожидать, что двойственность такого типа обнаруживается везде, где только появляет­ся постоянная Планка? Но тогда почти сам собой воз­никает вопрос: поскольку свойства электрона в стацио­нарном состоянии атома описываются с помощью кванта действия, не можем ли мы предположить, что и электрон так же двойствен, как свет?»

Напомню, что предположение о волновой природе света было выдвинуто еще Гюйгенсом и считалось до­казанным со времен Томаса Юнга и Огюста Френеля, но открытие Генрихом Герцем явления фотоэффекта, при котором кинетическая энергия, вырываемых светом из поверхности катодов электронов, не зависела от ин­тенсивности падающего света, а только от его частоты, и доказательство А. Эйнштейном прерывистой структу­ры света, поглощаемого отдельными порциями-квантами М. Планка, как бы свидетельствовали об одновременном наличии у фотонов света волновых и кор­пускулярных свойств, т.е. о дуализме свойств фотонов света. Постулирование дуализма свойств фотонов, а следом и электронов и остальных элементарных частиц, было положено в основу нарождающегося метода опи­сания природных явлений на микроуровне. И если в классической механике возможность исчезновения или возникновения «независимых» от тел свойств имела как бы случайный характер, то в квантовой механике эта случайность превращалась в закономерность, по которой частица мыслилась и «выступала» в одних взаимодействиях как частица, а в других как волна, и эти корпускулярно-волновые свойства оказывались не­зависимыми и от частицы и от пространства, в кото­ром она двигалась. И даже описание движения элемен­тарных частиц тоже как бы распалось на формализации корпускулярных и волновых уравнений квантовой ме­ханики, основой которых становилась постоянная Планка, и энергия Е излучалась телами не непрерывно, а строго определенными порциями:

Е = hv, (5.5)

где v - частота электромагнитного излучения.

Следует отметить, что порции электромагнитного из­лучения с энергией hv называют обычно квантами или фотонами, не имеющими массы покоя m = 0 (?? - А.Ч.), и глав­ное свойство, которое им приписывается, есть свойство двигаться в пространстве, при отсутствии внешних сил, прямолинейно и равномерно с абсолютной скоро­стью, равной скорости света. То есть по закону инер­ции. А потому, например, отражение фотонов от зерка­ла с углом падения, равным углу отражения, прои­сходит в квантовой механике чисто механическим образом, так же как и резинового мячика от ровной по­верхности.

Если квант действительно отражается от зеркала как мяч от стенки, то, как отмечается М. Канаревым в [ 33 ], должна существовать фаза перехода от абсолютной скорости до нулевой (в которой фотон находиться не может по определению) и возвращение от нуля к абсо­лютной, и этот отскок, связанный с гигантским возрастанием массы движения, не должна выдерживать ни одна «неделимая» частица. Однако согласно квантовой механике в этот момент масса фотона наоборот должна оказаться равной нулю, и он обязан исчезнуть. Но он не исчезает. Почему? И каков механизм данного перехода? Да и может ли фотон, пронизывающий молекулы ве­ществ, отскакивать от неровной поверхности тел?

Ответа на такие простые вопросы ни в рамках кванто­вой механики, ни в рамках релятивистской не находит­ся. Эти вопросы обходятся молчанием. Но молчание в данном случае не признак ясности, а признание непо­нимания сути явления. И это непонимание — следствие принятия инерционной формы движения фотонов.

Если же фотоны, как и все частицы, двигаются не по инерции, а посредством взаимодействия с окружающим атомно-молекулярным пространством, то, влетая из мо­лекул менее плотного пространства в молекулы более плотного, фотоны деформируются полем этих молекул, «прижимаются» к их ядрам, имеющим пятимерную плотность, и, облетев их (на манер наших комет с бес­конечным эксцентриситетом орбиты), раздеформиру-ясь, «выталкиваются» обратно в менее плотное про­странство почти под тем же углом, под которым влетели в молекулу. То есть момент «отскока» фото­на от стенки отсутствует, и ему нет нужды останавли­ваться. Вот почему чем более гладкую поверхность (зеркальное полирование) и большую плотность имеет отражающее тело, тем качественнее отражение света и меньше рассеивание.

Далее буду останавливаться только на «квантовых ис­тинах», извлекая их из различных источников и показы­вать, какие ошибки привели именно к квантовому объ­яснению данных явлений и как они могут быть объяснены с позиций русской механики. Естественно, что все «истины» в данной работе охватить невозмож­но, поэтому будет проводиться в основном качествен­ный анализ некоторых из них с точностью до трех зна­чащих цифр и при возможности с указанием тех экспериментов, которые могут подтвердить данное описание.

Начнем с волн Де Бройля? С волн, «связанных с лю­бой микрочастицей, отражающих природу микрочас­тиц» [ 88 ], другое название — «волны вероятности», а еще точнее [a1] «волны амплитуды вероятности» (??). О волнах Де Бройля и его уравнении пишут с восхище­нием, очень много и очень туманно, хотя тумана вроде бы быть не должно. Да и восхищаться есть чем. В ма­тематической формулировке это одно из наиболее про­стых и изящных уравнений квантовой механики:

R_n = h/m_ev_n, (5.6)

где R_n - длина волны Де Бройля, h - постоянная Планка, v_n - скорость электронов, т_е - масса элек­трона.

А вот физическое представление о «волне вероятно­сти» ясностью до сих пор не отличается. Сам Де Бройль предположил, что движущейся с определенной энерги­ей и импульсом элементарной частице можно сопоста­вить некоторую плоскую монохроматическую волну. (Уже в этом предположении совершенно неясно, поче­му сопоставить и волну чего? Воды? Воздуха? Эфира?) Современное трактование тоже не отличается четко­стью. Постулируется, что волна Де Бройля является «волной вероятности» (опять же — вероятности чего?) и уточняется для ясности — «волной амплитуды веро­ятности».

Естественно, что высказанное предположение по вол­не Де Бройля необходимо было подтвердить физически (экспериментами), математическими доказательствами и понятийным аппаратом. За эмпирикой дело не стало, и буквально через тройку лет К. Девисон и Л. Джеммер подтвердили гипотезу Де Бройля, а далее подтвержде­ния посыпались как из ведра и не оставили никаких со­мнений в том, что электрон имеет волновые свойства. Математики тоже не отставали, а вот с понятийным оформлением дело обстояло несколько хуже. Убеди­тельных доказательств вероятности волн Де Бройля мною не обнаружено. Более того, возможно, такие до­казательства вообще отсутствуют, поскольку их посту пировали ошибочно, пропустив при математическом анализе модели атома каузальность волн Де Бройля. Попробую показать простыми расчетами на примере движения электрона по орбитам атома водорода, что свойством вероятности волны Де Бройля не облада­ют. Что волна Де Бройля есть траектория одного вит­ка электрона вокруг атома. Именно траектория, а не орбиталь, и именно электрона-частицы, а не электрон­ного «облака в штанах».

Выпишем из [ 22 ] величины постоянной Планка h, боровского радиуса а_b, массы электрона т_е, его скоро­сти на боровсой орбите v_b и по формулам [95] рассчи­таем параметры а_п для, например 10 орбит, а также длину волны l_п для каждой орбиты:

а_п = n²h²/m_ee²; v_n = e²/nh, (5.7)

и занесем данные этого расчета в таблицу 10. Известно, что длина волны l_п равна:

l_п = 2pа_п. (5.8)

Зная радиус всех орбит, по (5.8) определим длину вол­ны электрона на этих орбитах и занесем в табл. 10 столбец 4. По скорости электрона v_b на боровской ор­бите (5.6) определяем, чему равняется длина волны l' Де Бройля у этой орбиты:

l' = h/m_ev_b = 3,326·10^-8 см.

Таким образом длина волны Де Бройля на боровской орбите совпадает с длиной самой орбиты в полном соответствии с формулой (5.6), и, следовательно, ради­ус движения электрона равен боровскому радиусу (столбец 5).

Имея эту информацию и полагая, что на всех орби­тах атома электроны движутся по одним и тем же зако­нам, по (5.6) и (5.8), определим, чему равна длина волны l¢ и радиус а' каждой орбиты и заполним соответст­венно столбцы 5 и 6 таблицы. Естественно, что в формуле (5.6) остаются два неизменных члена: посто­янная Планка h и масса электрона т_е.

Таблица 10

	а 10^-8	v 10^8	l 10^-8	l ' 10^-8	а' 10^-8	m 10^-27
	0,529	2,188	3,324	3,326	0,529	9,110
	2,117	1,094	13,30	6,658	1,060	4,555
	4,763	0,7293	29,93	9,979	1,602	3,037
	8,462	0,5470	53,17	13,30	2,117	2,279
	13,29	0,4376	83,50	16,63	2.647	1,814
	19,05	0,3647	119,7	19,95	3,176	1,518
	25,93	0,3126	162,9	23,29	3,705	1,301
	33,87	0,2735	212,8	26,61	4,235	1,139
	42,87	0,2431	269,4	29,94	4,765	1,125
	52,92	0,2188	332,5	33,26	5,294	0,911

Что же мы получили? Действительно, вычисленные по формуле Де Бройля (5.6) и (5.8) длины волн электро­на l_n (столбец 5) и радиус его расчетных орбит а_n' (столбец 6) не совпадают с аналогичными параметрами, получаемыми из (5.7), но не вероятностным образом. Длина радиусов орбит а_п (столбец 2) и волны l_п (стол­бец 4 ) повторяется в столбцах 5 и 6 под номерами, яв­ляющимися квадратной степенью номеров столбца 2, и никаких исключений из данного правила не прослежива­ется. А это однозначно свидетельствует о том, что данные числа отображают некоторую пропущенную ранее закономерность. И эта закономерность скрыва­ется в уравнении (5.6) либо за постоянной Планка, либо за массой электрона.

Если не учитывать регулярность повторения длин волн и радиусов в столбцах 5-6, то табл. 10 как бы сви­детельствует о том, что траектория электрона не зави­сит от его скорости, длина волны оказывается различ­ной при одной и той же скорости, сам электрон «может находиться с разной вероятностью на любом расстоянии от ядра», в большинство орбит ни одна волна не укладывается целое число раз, да и координа­ты электрона оказываются неопределенными. То есть налицо все факторы, свидетельствующие о вероятност­ном характере волнового свойства электрона, весьма напоминающем волну вероятности. Повторю еще раз, вероятность проявляется в единственном случае:если не заметить (или игнорировать) регулярное по­вторение в 5 - 6 -м столбцах радиусов орбит и длин волн из 2 -го и 4 -го столбцов. Но что будет, если это повторение принять во внимание?

Наличие повторения а_n и l_n в 5 и 6 -м столбцах свиде­тельствует о том, что в формуле (5.6), описывающей движение электрона, один из параметров h или т_е на каждой орбите меняет свою численную величину по за­конам квантования. Возникает вопрос: Какой же из этих параметров квантуется? Для ответа на этот вопрос надо выяснить, а нельзя ли образовать постоянную Планка изпараметров боровской орбиты?

ħ = a_bm_ebv_b, (5.9)

Получилось! Количественные величины параметров а_b, т_еb, v_b боровской орбиты находятся в такой про­порции, что их произведение равно постоянной Планка ħ, и, следовательно, это произведение есть инвариант (что ранее уже было показано по КФР). А это означает, что данные параметры, включая массу электрона, являются переменными величинами и изменение лю­бого из них сопровождается пропорциональным изме­нением остальных таким образом, чтобы их произве­дение оставалось неизменным, то есть оставалось постоянной Планка.

Однако в квантовой механике величина массы элек­трона постулируется неизменной, и потому постоян­ную Планка можно образовать только количествен­ными величинами параметров боровской орбиты. Это равнозначно доказательству того, что электрон на боровской орбите движется по одним законам, а на прочих орбитах по другим. Чтобы вероятностные факторы исчезли из описания волны Де Бройля, было необходимо снять постулирование неизменности массы электрона и его заряда на разных орбитах атомов.

Вот она — причина, которая привела физиков двадца­тых годов к признанию вероятностного характера дви­жения волн Де Бройля. К тому времени уже 20 лет как все физики знали, как знают и сегодня, что масса элек­трона и его заряд неизменны всегда. То, что эта неизменность постулируется, вероятно, забылось или не было принято во внимание. И потому обойти запрет ирассчитать массу электрона для всех орбит по той же формуле (5.6), похоже, не осмелился ни один физик. Так волна Де Бройля получила статус «волны вероят­ности». И было нарушено правило формирования па­раметров орбит по единому закону (отмечу еще раз, что постоянная Планка получается в структуре атома только по параметрам боровской орбиты). Аза всякое нарушение законов природы надо платить. Чем и как, выяснится далее.

Попробуем, не реагируя на постулат постоянства массы электрона, рассчитать ее для каждой из 10 ор­бит, преобразовав формулу (5.6) в вид:

т_еп = ħ/l_nv_n.

Результаты расчета занесем полужирным курсивом в столбец 7 табл. 10 и проанализируем, что же получи­лось.

Во-первых; структуру атомов и молекул образуют как электроны с целочисленными орбитами, так и электроны с промежуточными орбитами.

Во-вторых; параметр т_еп, а вместе с ним и е_n, оказал­ся величиной переменной.

В-третьих; полностью исчезла какая бы то ни было вероятность в движении электрона. Длина волныl_п, радиус (координата) а_п, скорость v_n и масса т_п стали строго определенными для каждого электрона, а вели­чины параметров а' и l' оказались невостребоваными.

В-четвертых; электроны на всех орбитах движутся по траекториям и по одним законам.

В-пятых; появилась всеобщая инвариантная взаимосвязь параметров:

v_n/m_n = const, m_n²a_n = const₁, a_nv_n² = e_n²/m_n = const₂, m_nv_na_n= e_n²/v_n = const₃,..., ит.д.

В-шестых; постоянная h становится простым инвари­антом квантовой механики.

В-седьмых; боровская орбита приобрела статус рядо­вой (безномерной) орбиты.

---

Дата добавления: 2015-07-11