Взаимодействие тел в эфир­ном пространстве обусловливает им равное и про­тивоположное противодействие. 6 страница

Попробую показать физическую и логическую проти­воречивость данной формулировки, а также отсутствие в ней определения физической сущности силы инерции. Суть этой формулировки заключается в словах: «Удер­живает свое состояние...»

Но «удерживать свое состояние покоя или равномер­ного прямолинейного движения» по механике возможно только в том случае, когда тело не «предоставлено са­мому себе», а находится среди «истинно неподвижных» или «истинно подвижных» тел, т.е. передвигается мимо них или испытывает на себе их воздействие. А так как у Ньютона нет объективных свидетельств о состоянии движения тел, то приходится, указывая пальцем, опре­делять, какие тела в пространстве «истинно покоящие­ся», а какие движущиеся относительно «истинно покоя­щихся». И сам Ньютон сетует на то, что и в этом конкретном случае, когда тела перед глазами, не исклю­чена ошибка в определении движения тела или его по­коя. Тем более она возможна, когда «тело предоставлено самому себе», и только опять же мысленно мы можем представлять, что оно «предоставлено самому себе». Но такое мысленное представление еще не означает, что те­ло находится само по себе и для себя в состоянии покоя или равномерного и прямолинейного движения, по­скольку это мысленное представление не есть доставка этого же тела из места, подверженного воздействию гравиполя, в место, где гравиполе отсутствует, ну как, например, груза на паровозе. И мы не можем, как для груза, заранее сказать, что это тело после такого пере­мещения останется тождественным само себе.

Мысленно же, вслед за Ньютоном, и до сего времени предполагается, что, совершив телепортацию из грави­поля во вне гравиполя, тело, как огурчик с поля, оста­нется само собой, чтобы демонстрировать нам прямоли­нейное (опять же мысленное) и равномерное (и снова мысленное) движение, которое по Ньютону невозможно обнаружить даже мысленно.

В этих мысленных операциях как-то забывается, что свойство «напряженность гравитационного поля» при­суще не только внешнему пространству, но и самому телу, что оно такое же врожденное свойство мате­рии, как и все остальные свойства, и без него простран­ство просто не существует. Что внешнее гравиполе такой же атрибут тела, как и его собственное грави­поле, и по этой причине исчезновение внешнего гравипо­ля равносильно исчезновению заключенного в нем тела. А посему все рассуждения, включая математические, о движении тела вдали от гравитационного поля, как и от гравитирующих масс, которыми охотно и часто балуют­ся физики, есть фикция, игра воображения, способная дать постную пищу уму, но не предлагающая никакого механизма объяснения инерции.

Покажу невозможность существования пробного тела вне гравиполя на примере подъема его с поверхности Земли и с перенесением на бесконечное расстояние R → ∞, на котором напряженность внешнего гравиполя стре­мится к g → 0. Эта зависимость описывается инвариан­том (3.65):

R²g – const,

и отсюда при

R →∞, g → 0.

С возрастанием расстояния между гравитирующим телом и пробным напряженность внешнего гравиполя уменьшается и на бесконечности обращается в 0, что и требовалось доказать для подтверждения невозможности отсутствия гравиполя по механике Ньютона.

Аналогичные доказательства часто фигурируют, есте­ственно математически более насыщенные, в теоретиче­ской физике. Однако они фигурируют как отдельные самостоятельные уравнения или группы уравнений, не связанные с другими свойствами систем, которые опи­сывают. Следствием является одностороннее понимание результатов доказательства. КФР все свойства связывает системно и, потому изменение одного свойства, позво­ляет определить, как это изменение отразится на других свойствах. Например, на массе т тела. Расстояние R свя­зано с массой т инвариантом

Rm² – const,

и при

R → ∞, т → 0,

т.е. вместе с возрастанием расстояния от Земли до пробного тела, масса последнего будет уменьшаться и при R = ∞ станет т = 0. Таким образом, масса пробного тела, а вместе с ним и само тело, исчезает на бесконечности. Следова­тельно, формализован-ная система зависимости между параметрами взаимодейст-вующих тел приводит к тому же выводу, к которому привела диалектика качествен­ного анализа.

Все эти рассуждения потребовались для того, чтобы показать, что свойство инерции, понимаемое в механике как движение без взаимодействия, есть логический про­счет, ибо уже сама формулировка, включающая поня­тие «способность сопротивления», предполагает нали­чие некоторого взаимодей-ствия с пространством, какого-то механизма зацепления или удержания, посред­ством которого и происходит противодействие, некое «стремление» к сохранению телом своего состояния. И до тех пор, пока этот механизм не будет найдет и объяс­нен, представление об инерции будет оставаться пута­ным, неконкретным, туманным, и никакая формулиров­ка закона инерции не будет адекватна его природному аналогу.

Само представление о возможности прямолинейного движения возникло как следствие экстраполяции на­блюдаемого иногда в природе, относительно короткого, вызываемого искусственно, прямолинейного движения тел, на область вымышленного пустого пространства.

Вывод о возможности кратковременного искусствен­ного равномерного и прямолинейного движения следо­вал из некоторых экспериментов Галилея, и они-то по­служили основой Ньютону для использования в законе инерции.

Представление о равномерном прямолинейном дви­жении предполагает возможность движения без дви­жущего тела и существование независимых свойств движения. Оно придало скорости статус самостоя­тельного свойства, не связанного с ускорением и не за­висящего от него, а ускорению — возможность исче­зать при мыслимом равномерном движении.

Естественное, прямолинейное равномерное движение в природе не наблюдается вовсе. Это прямое следствие того, что все пространство пронизано гравитацион­ным излучением, не существует вне этого излучения и живет этим излучением. Тела же, движущиеся в гра­витационном пространстве под его воздействием, все­гда изменяют траекторию своего движения и потому принципиально не могут двигаться прямолинейно и рав­номерно. Именно это обстоятельство потребовало уда­ления движущегося по инерции без взаимодействия тела из гравитационного поля. Последнее же было возможно опять-таки только при вольном допущении, что тела не взаимодействуют с гравиполем, и по этой причине каче­ственно не меняются при удалении из него. Круг замк­нулся.

Вопрос об относительности движения с постоянной скоростью как о движении без взаимодействия мог воз­никнуть только при механистическом подходе к объяс­нению свойств и зависимостей природы. Этот вопрос предполагает существование независимых свойств, от­сутствие взаимодействия тела с пространством как в статике, так и в динамике, а, следовательно, самото­ждественность тела в состоянии относительного по­коя и движения, возможность прямолинейного движения, исчезновения гравитационного поля и неизменность тела в отсутствии гравитационного поля. Все эти по­сылки — прямое следствие экстраполяции выводов, сде­ланных на борту движущегося равномерно большого корабля, и не предполагают никаких качественных раз­личий в состоянии движущихся тел.

В соответствии с принципами диалектического мате­риализма качественные изменения играют определяю­щую роль в понимании процессов взаимодействия. В природе нет не взаимодействующих систем, и всякое движение есть либо следствие некоего взаимодействия, либо само по себе взаимодействие. Поэтому тело, по­коящееся на поверхности другого тела (например, в за­крытой тележке на поверхности Земли), имеет одну форму взаимодействия с ней, одно количество само­движения, одно качественное состояние. То же самое тело, движущееся с постоянной скоростью относи­тельно Земли, имеет другую форму взаимодействия, другое количество движения и иное качественное со­стояние. Оно не тождественно само себе. Все это вы­текает из диалектики. Однако данные диалектические рассуждения ничего не значат для физиков, если за ни­ми не будет стоять предложение конкретного экспери­мента, а лучше нескольких экспериментов, переводящих полуабстрактные, качественные, логически последова­тельные рассуждения в сухую эмпирику экспериментов. Позволяющих превратить качественную систематику в количественные сравнения достигнутых в опыте изме­нений показателей параметров тел в состоянии покоя и прямолинейного движения с постоянной скоростью.

Надо отметить, что именно абсолютная уверенность физиков в невозможности обнаружения равномерного движения тела приборами, находящимися внутри него, и стала причиной того, что такие эксперименты не проводились, ибо и без них теоретически ясно, что при­боры информации о движении не принесут. А потому их проводить — только деньгами сорить. Естественно, что деньгами сорить не стали. В результате этой уверенности три столетия никто не удосужился повторить экспе­рименты Галилея с использованием даже не капель воды и летающих мух (хотя и без экспериментов понятно, что в равномерно движущемся теле ни одна капля с потолка не попадет в то место, в которое она попадает в непод­вижном), а хотя бы гироскопа Фесселя или обыкновен­ного маятника, не говоря уже о более точных приборах.

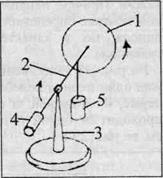
Гироскоп Фесселя (рис. 34) представляет собой ротор 1, укрепленный на оси 2, которая свободно ставится на острие стойки 3. На противоположной от ротора стороне оси 2 устанавливается противовес 4, и ось может гори­зонтально вращаться. Когда ротор гироскопа раскручи­вается до стандартных оборотов, к оси подвешивают не­большой перегрузок 5, и под его воздействием гироскоп начинает прецессировать. При установившейся горизонталь­ной прецессии практически не будет наблюдаться нутации. Если теперь использовать этот гироскоп в тележке, а тележку двигать с постоянной скоро­стью, то уже при равномерной скорости в несколько десятков сантиметров можно будет на­блюдать регулярную нутацию ротора с максимумами и ми­нимумами в направлении движения

Рис. 34. и перпендикулярно ему. Эта нутация и регистрирует равномерное движение тела по поверхности, а, следовательно, и его абсолютность.

Выше уже упоминалось, что обыкновенный отвес не занимает вертикального положения в тележке, движу­щейся с постоянной скоростью, но и не изменяет при движении угол своего наклона, а это и есть показатель абсолютности движения тележки с постоянной скоро­стью. Отклонение отвеса обеспечивается «уплотнением» эфира, а вместе с ним и напряженности внешнего гравиполя движущимся телом. И следствия «уплотнения» будут фиксироваться самыми различными приборами, включая простейший из них физический маятник. Рас­смотрим качественно взаимодействие с гравиполем ма­ятника, колеблющегося в тележке, движущейся с посто­янной скоростью.

Прежде всего, для тела, движущегося горизонтально с постоянной скоростью во внешнем гравитационном по­ле, последнее, как уже говорилось, не остается однород­ным для качающегося грузика-маятника, в то время как для самой тележки оно остается «уплотненно» однород­ным. Поэтому фиксировать движение любого тела с постоянной скоростью можно только такими прибо­рами, которые совершают собственное движение как относительно пространства, так и относительно те­лежки. Причем, например, угол отклонения отвеса в та­кой тележке определяет как характер «уплотнения» гравиполя, так и характер колебания маятника в этом гравиполе.

На рис. 35 качественно, без разбивки на такты, отра­жен один период колебания маятника в движущейся те­лежке, проходящей за единицу времени 1 см (маятник проходит от одной точки до другой, нумерацию точек см. на рис. 29).

Из рисунка 35 следует, что на протяжении одного пе­риода на каждом отрезке пути маятник имеет относи­тельно Земли, а, следовательно, и относительно гравиполя, различную скорость движения, которая складывается

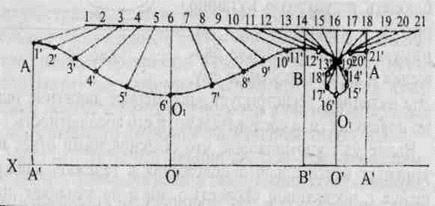
Рис. 35

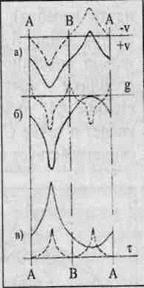
из скорости движения тележки и скорости колебатель­ного движения маятника. Проектируя скорости на ось XX получаем, что на участке АВ скорости тележки и ма­ятника складываются, а на участке ВА — вычитаются. Следовательно, в отличие от неподвижного относительно пространства маятника, у движущего полупериоды асимметричны. Асимметрия вызвана различными скоростями движения маятника относительно внешнего гравиполя, регистрируется по всем параметрам колебания и легко рассчитывается. На рис.36 графически изображено изменение парамет­ров направления и скорости v движения маятника, на­пряженности его гравиполя g, и периода колебаний τ в неподвижной тележке (штрихами) и в движущейся (сплошными линиями). На графике фиксируется четкая симметрия изменения параметров v, g, τ у маятника, колеблющегося в неподвижной тележке. Совершенно иная картина наблюдается при коле­бании в тележке, движущейся с по­стоянной скоростью. Все рассматри­ваемые параметры v, g, τ резко асимметричны. Отмечу, что асим­метрия не наблюдается при колеба­нии маятника в плоскости, перпен­дикулярной движению тележки. Асимметрия полупериодов коле­бания в плоскости движения позво­ляет эмпирически, находясь в закры­той тележке, определить состояние ее покоя или движения. Более того,
анализ других особенностей колебания позволяет в принципе найти скорость движения тележки, направление ее движения, массу и радиус тела или пространства, по которому

она движется. А это означает, что движение с постоянной скоростью абсолютно, а не относительно.

Вернемся к эксперименту, который Галилей проводил «в зале под палубой

какого-нибудь большого корабля».

Естественно, что технические возможности средневековья не могли обеспечить тех скоростей и той высоты помещения, которые потребовались бы для фиксации, например, отклонения от вертикали падающей из круж­ки капли воды. Чтобы это отклонение зафикси-ровать, необходимо «кружку» подве-сить на мачте, на высоте 200-250 м, воду заменить мелкой дробью, равно- Рис. 36. мерную скорость корабля держать где-то 25-30 м/с. Что и сейчас на пределе технических возможностей. И если при дви­жении такого корабля с верхушки мачты уронить дро­бинку, то в своем падении она отклонится вперед по хо­ду больше чем на 0,5 мм. Последнее будет зафиксиро­вано приборами и подтвердит, что движение с постоянной скоростью абсолютно, а не относительно.

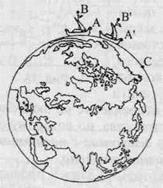
Абсолютность равномерного движения по поверхно­сти обусловлена тем, что фигура Земли не плоская, а круглая. И точки протяженного предмета (например, мачты корабля), находящиеся на разном расстоянии от центра Земли, будут иметь различную скорость относи­тельно поверхности. Поэтому если за время падения дробинки с мачты (рис. 37) ее основание пройдет рас­стояние АА, то верхушка — расстояния ВВ', и дробинка упадет в точке С, пройдя расстояние АС = ВВ'. А это и свидетельствует о движении корабля.

Рис. 37

Галилей, по-видимому, исходил из того, что изме­нения, происходящие в дви­жущемся теле, можно фик­сировать ощущениями. И, не уловив заметных отклоне­ний в поведении тел внутри корабля, он сделал вывод, что равномерное движение по криволинейной поверх­ности является относитель­ным. Именно поэтому прин­цип относительности распростра-нялся им только на круговые движения.

Это была формальная ошибка. Ее многократно усугу­бил Ньютон, распрямив круг и постулировав гипотезу об относительности прямолинейного равномерного движения. Именно прямолинейное движение названо позже А. Эйнштейном принципом относительности Галилея, хотя в действи­тельности он сам является его автором.

В результате в механике оказалось не просто две ошибки в понимании движения как процесса взаимо­действия, но и утвердилось как естественное понятие прямолинейности, никогда и нигде не подтвержденное экспериментально. Гипотеза прямолинейного и равно­мерного движения без взаимодействия постепенно стала единственной сущностью инерции. С одной сто­роны, она как бы объясняла само явление инерции, а с другой — превратилась из гипотезы в реальный факт относительности, не требующий подтверждения своей истинности.

Можно предложить проведение других эксперимен­тов, способных регистрировать иными приборами дви­жение с постоянной скоростью, например атомными ча­сами, гироскопами, световыми лучами и т.д., и все они будут подтверждать качественное отличие тела непод­вижного от движущегося.

Используемый классической механикой, как и теорией относительности, принцип относительности движения с постоянной скоростью полностью не вписывается в за­коны диалектики. Не вписывается потому, что состоя­ние покоя, т.е. то состояние, в котором центр масс од­ной системы не изменяет своего положения относительно центра масс другой, отличается от со­стояния движения в пространстве в первую очередь изменением качества. Представление о том, что про­странственное движение есть изменение качества и снова изменение качества, отсутствует как у Ньюто­на, так и у Эйнштейна. Вот это не наличествующее в механике свойство изменения качественного состояния при перемещении из одного места пространства в дру­гое необходимо использовать для эмпирического определения состояния движения. Причем все свойства тела в движении меняются, но меняются в различной про­порции и по-разному в направлении движения и ортого­нально ему. И эти изменения совершенно одинаковы как для «медленных», так и для «околосветовых» скоро­стей. Только эффективность качественного изменения свойств при этом, естественно, будет проявляться с раз­ной степенью наблюдаемости, да и наблюдения будут проводиться другой категорией приборов [41].

Именно уверенность Ньютона и позднее Эйнштейна в невозможности качественных изменений тел при отно­сительном движении, поддержанная научным сообщест­вом, стала психологической преградой на пути любых эмпирических проверок относительности движения. Они не рассматривались и не ставились не потому, что бы­ли невозможны для физического исполнения, а потому, что были невозможны постулативно. Физические по­стулаты превратились в ученый догмат, более жесткий и более действенный, чем догматы общественные и цер­ковные. Научный общественно-психологический запрет более жестко давит на личность, чем любые кандалы и запоры. Он сковывает мысль. Он запрещает вольный полет фантазии. Он навешивает шоры на разум и тормо­зит развитие и науки и общества.

Однако развитие науки со скрипом продолжается. По­являются эксперименты, не влезающие в обусловленные запретом ворота и потому отвергаемые ортодоксами с порога. (Вдумайтесь — факты в физике отвергаются только потому, что они противоречат запретительным постулатам.) Однако количество таких экспериментов накапливается. Их уже неудобно «заметать под поло­вик», велика становится куча, и делается как-то уже слишком непристойно использование в качестве основ­ного аргумента популярной шуточки «этого не может быть». Появляется необходимость, превращающаяся в потребность — объяснить, какова природа этих ненуж­ных и даже неприличных экспериментов, без наруше­ния запретов, без разрушения сложившейся ошибочной системы мышления. И чтобы миновать запрет незави­симо от того, понимают ли это исследователи или нет, разрабатывается мощный математический аппарат (как, например, в квантовой механике), сшивающий некорректные постулаты и подменяющий реальное понимание физических взаимодействий системой очень точных математических операций, подгоняющих решение под необъяснимые эксперименты. Конвенционализм математики обусловливает возможность такого развития фи­нки.

В качестве примера сшивания рассогласованных теорий можно привести также работу И. Пригожина «От существующего к возникающему». В ней для объясне­ния необратимости физических процессов, на основе сложного математического аппарата (потребовались супероператоры, стохастическая формализация с введени­ем вторичного времени и функционального не геометрического пространства) проводится достаточно формальное внесистемное самосогласование между динамикой и термодинамикой. И делается это с постулированием второго начала в качестве основополагающего динамического принципа, определяющего направление стрелы времени. Однако в этом аппарате отсутству­ет качественное изменение при взаимодействиях и ме­ханизм необратимости. Представление о механизме физических процессов подменяется математической символикой. Понимание сути физических явлений тоже ухудшается. И, следуя Бриллюэну [63], теория (напри­мер, теория относительности или квантовая механика) превращается в математическую фантастику, не имею­щую предсказательной ценности, а, следовательно, и пользы. Поскольку у теории нет способов предсказания введения тел в процессе физических взаимодействий, то не возникают и идеи экспериментов, подтверждаю­щих или опровергающих теорию. И все обсуждаемые к проведению эксперименты обкатываются в рамках заве­домо некорректных постулатов, образующих понятий­ный базис классической механики и всей физики.

3.6. Движение, ускорение, инерция

Наиболее сложными и наименее понятными пробле­мами механики Ньютона являются проблемы, связанные с движением, ускорением и инерцией. И хотя большин­ство ученых не сомневается в полной разработанности этих проблем и однозначного физического толкования их сущности (ведь существует четкий и отработанный математический механизм, описывающий количествен­но все нюансы движения тел в пространстве), эта уве­ренность — еще не основание для объяснения движения без взаимодействия, его сущности, возможности прямо­линейного движения с постоянной скоростью по инер­ции (относительное движение) и движения с ускорени­ем. Эта уверенность постулируется и может оказаться не описанием реального природного процесса, а только ос­новой для подгонки математического аппарата под оп­ределенные эмпирические данные. Гносеологические корни относительного и абсолютного движения остают­ся скрытыми и неясными для понимания, а, следователь­но, и для формализации процесса движения. Это следст­вие того, что в механике Ньютона нет онтологического ответа на вопросы: что есть движение и откуда оно бе­рется? Возможно ли существование прямолинейного движения по инерции как движения без взаимодейст­вия? Чем и как вызывается инерция? Возможно ли дви­жение тел в отсутствии гравитационного поля? Вопро­сов возникает очень много, и они требуют детального описания сущности механизма движения.

Как было показано выше, самодвижение тел — пуль­сация, является основой всех видов движения, вклю­чая перемещение относительно пространства, взаи­модействия с последним и вращение. Рассмотрим движение тела, например, стального шара радиусом – 25 см, плотностью ρ = 7,9 г/см³ по поверхно­сти без трения и с учетом его взаимодействия с вращающимся гравиполем Земли. Объем шара V = 6,54·10⁴ см3, масса т = 5,2·10² г, а вес Р = 5,168·10⁵ см.г.с^-2. Когда шар лежит на поверхности относительно неподвиж­но (т.е. его центр масс не перемещается по поверхности, а собственные колебания симметричны, не обеспечива­ют его перемещение и не принимаются во внимание), то все его параметры сбалансированы с параметрами Зем­ли. Ее везде принимаем невращающейся сферой с ра­диусом R = 6371 км и не имеющей атмосферы.

Шар, лежащий на поверхности, сам по себе не свобо­ден от нагрузок. Его объем сжат силой F, равной силе веса Р, но никакими приборами и измерениями это дав­ление не определить, поскольку ему подвергаются все элементы измерительных приборов. Именно это давле­ние есть следствие воздействия внешнего гравиполя на тело, и точно с таким же усилием тело сопротивляется внешнему давлению. Причем сопротивление грависжатию определяется свойствами тела, его структурой и строением и проявляется в некотором подобии форме силы Гука.

Важно понимать, что для внешнего наблюдателя вес тела есть его давление на поверхность Земли, а для самого тела вес — внешняя сила, обусловливающая ве­личину его деформации. То есть изменение параметров тела под воздействием гравиполя Земли является причиной возникновения веса.

Начнем разгонять тело по поверхности с постоянным ускорением и доведем скорость v движения до орби­тальной v' = 7,91·l0⁵ см/с. В процессе разгона вес тела Р, как это следует из классической механики, « уменьшается», а масса возрастает, что вовсе не следует из той же механики, и, при достижении первой космической скорости, становится равным 0. Естественно, что в процессе разгона меняются все свойст­ва тела, но механика Ньютона фиксирует только изме­нение силы притяжения и совершенно не объясняет физический механизм, вызывающий это изменение. Попробуем разобраться в этом вопросе.

По механике: при разгоне тела возникает ускорение а', направленное вер­тикально вверх и равное

а' = – v²/R.

Оно создает телу дополнительную подъемную силу F':

F' = – та'.

При достижении ускорением а величины ускорения свободного падения а = g подъемная сила F' становится равной весу шара Р. Происходит их взаимное погаше­ние:

P – F' = 0.

И в шаре, движущемся с первой орбитальной скоро­стью, возникает кажущееся состояние невесомости. Этот сценарий как бы подтверждается каждодневно демонстрацией невесомости космонавтами на космических кораблях. И потому указанное объяснение не вызывает никакого сомнения в своей справедливости. Но что произойдет, если усомниться в этом объяснении? И что может вызывать сомнение?

Сомнение вызывает исчезновение той силы — веса, которая является атрибутом тела. Т.е. не может исчезнуть по определению. Если же она исчезла, то и тело, в структуру которого входит эта сила, тоже исчезло, и все предыдущее объяснение являются математическими манипуляциями и становится некорректными.

Как уже говорилось, вес тела обусловлен силой, с которой оно сжимается напряженностью g гравиполя Земли. Когда тело начинает двигаться, возникающее ускорение а (дополнительная напряженность, вызываемая уплотнением гравиполя Земли) не отнимается, а прибавляется к напряженности внешнего гравиполя. И сила сжатия возрастает:

F' = mа'.

И потому движущееся с ускорением тело воспри­нимает возникшую силу F' как дополнительное сжи­мающее воздействие, вызывающее пропорциональное возрастание деформации. К силе веса Р = F, действующей на него в статическом состоянии, при движении стала добавляться сила F' которая при орбитальной скоро­сти сравнивается с силой F = F' и на тело действуют две силы:

F + F' = 2 F = 2 Р.

Это дополнительное воздействие напряженности гравиполя на движущееся тело, обусловленное взаимодействием тела с эфирным пространством, вызывает изменение всех его свойств. Подчеркну, что собственный инвариант свойств шара для сжимающей силы F и в статическом и в динамическом состоянии не меняется. Внешняя си­ла F' изменяет количественную величину свойств, но не внутренние взаимосвязи. Используя это качество, нахо­дим по КФР для шара инвариант, связывающий радиус r с силой F в статике:

F²r⁵= 2,608·l0¹⁸ – const. (3.70)

Поскольку инвариант (3.70) остается неизменным как для статики, так и для динамики, то с изменением силы F до 2 F величина const не изменится, но вместе с силой изменяются количественно все свойства тела, включая его радиус r. Определим, как изменится величина радиуса r' при движении шара с орбитальной скоростью подставив в F²r⁵ = 2,608х10¹⁸ величину 2 F = 1,0336·10⁶, и решив относительно r' получаем:

r' = 1,895·10 см.

Таким образом, приобретение телом орбитальной скорости сопровождается деформацией его радиуса почти на четверть размера в статическом состоянии. Это важнейший результат для понимания диа­лектики движения тела во внешнем гравитационном поле. Именно им определяются все физические процес­сы, сопровождающие движение. Именно он является подтверждением качественного и количественного из­менения состояния тела при переходе от статики к динамике. И именно отсюда следует физическое пред­ставление о механизме движения с ускорением и дви­жении по инерции.

Рассмотрим, как изменяются количественно другие свойства движущегося тела, например масса т и напря­женность гравиполя g. Связь массы с радиу­сом определяется инвариантом:

Дата добавления: 2015-07-11