Критерии устойчивости

Для того чтобы решить устойчиво или неустойчиво равновесие механической системы, в настоящее время используются различные критерии устойчивости, такие, например, как: динамический, статический, энергетический и другие.

Наиболее общим критерием к изучению устойчивости положения равновесия в механике является энергетический критерий, основанный на исследовании изменения полной потенциальной энергии системы при отклонениях от положения равновесия.

Согласно энергетическому критерию, если полная потенциальная энергия системы имеет минимум, то равновесие системы устойчиво, если максимум, то неустойчиво, безразличному равновесию соответствует постоянная величина энергии. Полная потенциальная энергия складывается из внутренней энергии собственно системы и работы внешней нагрузки и определяется по (4.9)

, (4.9)

где – приращение потенциальной энергии;

– приращение за счет работы внешних сил;

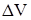– приращение внутренней энергии.

Если , то система устойчива, и значит внутренней энергии достаточно, чтобы вернуть систему в состояние равновесия, если , то система неустойчива, и значит внутренней энергии недостаточно, чтобы вернуть систему в состояние равновесия, и в случае, когда , имеем безразличное состояние равновесия.

Также широкое применение получил статический критерий устойчивости. Согласно ему неустойчивость системы характеризуется появлением смежной формы равновесия, бесконечно близкой к ее исходной форме. В результате этого предположения анализ устойчивости форм равновесия оказывается полностью в сфере вопросов статики.

Статический критерий в основном применяется к консервативным системам. В линейной теории упругости уравнения равновесия составляются для недеформированных систем. Смежные формы равновесия могут быть обнаружены только в том случае, когда уравнения равновесия составляются для деформированной системы, отклоненной от своего ненагруженного положения системы.

Применение данного критерия для определения критической нагрузки рассмотрим на примере стержня. Покажем, так же, в каком случае появляются смежные состояния равновесия, то есть при одних и тех же внешних нагрузок и условиях закрепления упругая система может иметь не одно, а несколько состояний равновесия.

Рассмотрим, жесткий стержень длиной l, один конец которого закреплен в упругом шарнире, а другой нагружен вертикальной силой Р как показано на рисунке 4.2.

Рисунок 4.2 – Схема нагружения стержня

В исходном ненагруженном состоянии ось стержня строго вертикальна. Составим уравнение равновесия для отклоненного состояния. При отклонении стержня сила Р сохраняет вертикальное направление. Момент в упругом шарнире будем считать пропорциональным углу отклонения стержня 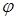и равным

, (4.10)

где k – жесткость упругого шарнира.

Тогда записав уравнение равновесия стержня в отклоненном от вертикали состоянии, получим

, (4.11)

или

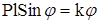. (4.12)

Полученное уравнение имеет два независимых решения:

1) 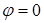при любом значении Р;

2) .

Кривая, соответствующая этим решениям при 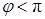, показана на рисунке 4.3, где по оси ординат отложены значения безразмерной силы P. Как видим, при единственно возможным будет исходное вертикальное положение равновесия. При наряду с исходным вертикальным положением равновесия стержня (j=0) становятся возможным и другие положения равновесия при j¹0. Например, при Р = Р₁ возможны три различных положения стержня, соответствующие точкам 1, 2, 3. Точка 2 соответствует вертикальному положению, а точки 1 и 3 – отклоненным положениям равновесия. Если рассмотрим поворот стержня на произвольный угол j, то увидим что с ростом абсолютного значения безмерной силы Р число возможных положений равновесия неограниченно возрастает.

Рисунок 4.3 – Кривая нагружения

Какие из указанных выше положения равновесия – устойчивые и какие неустойчивые?

Как установлено, исходное вертикальное положение равновесия стержня остается устойчивым до . При стержень не сможет остаться в исходном положении и отклоняется вправо или влево. Таким образом, при переходе через точку А исходное положение равновесия стержня перестает быть устойчивым. Точки на оси ординат, лежащие ниже точки А соответствуют устойчивым состояниям, а выше – неустойчивым. Точка А называется критической точкой, а соответствующее ей значение нагрузки – критическое.

Кроме того, в точке А пересекается ось ординат, соответствующая исходному положению равновесия, с кривой, соответствующей отклоненному положению равновесия. Такие точки, в которых решение расщепляется на две ветви, называются точками бифуркации или точками ветвления решений. В нашем случае точка бифуркации совпала с критической точкой.

В точке бифуркации исходная устойчивая форма равновесия сменяется другой устойчивой формой равновесия. Это критическая точка бифуркации первого типа. В критической точке бифуркации второго типа исходная устойчивая форма равновесия сменяется другой неустойчивой формой равновесия.

Согласно динамическому критерию исходная форма движения или равновесия системы устойчива, если малые возмущения вызывают малые отклонения системы от этой формы, которые могут быть сделаны как угодно малыми при уменьшении возмущений. Система будет неустойчивой, если даже сколь угодно малые возмущения вызывают конечные отклонения системы от ее исходной формы.

В том случае, когда применяется динамический критерий устойчивости, рассматриваются не формы равновесия, мало отличающиеся от заданной, а изучаются законы движения системы после того, как ей было сообщено некоторое отклонение от исходного состояния. Если движение происходит так, что исходное положение равновесия восстанавливается, то это положение считается устойчивым.

Дата добавления: 2015-07-11