
Читайте также:
|
РАСЧЕТ АППАРАТОВ НА УСТОЙЧИВОСТЬ ФОРМЫ
Общие сведения
Понятие об устойчивости. Критические нагрузки
В настоящее время нет четкого определения устойчивости. В разной литературе приводятся отличные друг от друга формулировки. Причем понятия отличаются в зависимости от того, какой критерий взят за основу при рассмотрении данной проблемы. Так, например, под устойчивостью понимается свойство системы сохранять свое состояние при внешних воздействиях. Если система таким свойством не обладает, она называется неустойчивой. Под потерей устойчивости понимается резкое качественное изменение характера деформаций элемента конструкции, происходящее при определенном значении нагрузки. Также под потерей устойчивости понимают резкое качественное изменение первоначальной геометрической формы элементов оборудования.
Как оказывается, при некоторых определенных значениях внешних сил упругая система может иметь несколько положений равновесия, причем одни из них будут устойчивыми, другие неустойчивыми. В развитии данного подхода говорится о множественном положении равновесия, а в задачу теории упругой устойчивости входит определение условий при которых становится возможным различное состояние равновесия системы, установление форм равновесных конфигураций и выяснение того, какие из конфигураций соответствуют устойчивым состояниям равновесия, а какие нет.
Что же происходит с системой при потере устойчивости? В реальных условиях всегда существуют какие-то причины, по которым может произойти отклонение от исходного равновесного состояния. Следовательно, возможность перехода к новому состоянию в неустойчивой системе всегда реализуется. В этом случае говорят, что произошла потеря устойчивости.

Колонный аппарат с ребрами жесткости
Система при потере устойчивости может вести себя по-разному. Обычно происходит переход к некоторому новому положению равновесия, что в подавляющем большинстве случаев сопровождается большими перемещениями, возникновением пластических деформаций или полным разрушением. В некоторых случаях при потере устойчивости конструкция продолжает работать и выполняет по-прежнему свои основные функции, как, например, тонкостенная обшивка в самолетах. Возможны, наконец, и такие случаи, когда потерявшая устойчивость система, не обладая устойчивым положением равновесия, переходит в режим незатухающих колебаний.
Кроме этого существуют некоторые случаи потери устойчивости, которые не вписываются в классическую схему. По одному из определений, положение равновесия считается устойчивым, если при любом, сколь угодно малом отклонении система, предоставленная сама себе, возвращалась в исходное положение. Если же система по устранению причин, вызывающих это малое отклонение, не возвращалась в исходное положение, то говорится, что это положение равновесия является неустойчивым. Так или иначе, во всех случаях предполагается, что отклонения от положения равновесия являются не только малыми, но сколь угодно малыми. В связи с этим иногда употребляют выражение «система устойчива в малом». Это значит, что при любом, сколь угодно малом отклонении от положения равновесия предоставленная сама себе система вернется в начальное положение. Вместе с тем остается открытым вопрос, вернется ли в начальное положение система, если ее отклонить «посильнее», то есть дать не сколь угодно малое, а просто малое, но конечное отклонение. Оценка устойчивости при этом условии носит название оценки устойчивости в большом. Система, устойчивая в большом, устойчива и в малом, но обратное утверждение, естественно, неверно. Система, устойчивая в малом, может оказаться неустойчивой в большом.
Исследование устойчивости упругих систем в большом много сложнее, чем в малом, поскольку в этом случае решение задачи сводится к исследованию нелинейных уравнений. Однако решение задач устойчивости в такой постановке дает возможность ответить на вопросы, которые с позиций малых перемещений не могут быть решены вовсе.
Особое значение приобретают вопросы устойчивости в большом при исследовании оболочек. В частности, задача об устойчивости сферической оболочки, находящейся под действием внешнего давления, и цилиндрической, сжатой в осевом направлении, получает удовлетворительное объяснение лишь с позиции устойчивости в большом.
Явление потери устойчивости для упругих тел можно наблюдать на целом ряде примеров. Наиболее простым случаем является потеря устойчивости центрально сжатого стержня. При достаточно большой силе стержень не может сохранять прямолинейную форму и неминуемо изогнется. Произойдет потеря устойчивости.
Тонкостенная труба, нагруженная внешним давлением, способна потерять устойчивость. При этом круговая форма сечения переходит в эллиптическую, а затем труба сплющивается, хотя напряжения к моменту потери устойчивости далеко не достигают предела текучести. Та же труба может потерять устойчивость и при осевом сжатии, и при закручивании.
Обобщая сказанное, следует отметить, что наиболее ярко явление потери устойчивости проявляется в легких тонкостенных конструкциях: в сжатых оболочках и тонких стенках. Поэтому при проектировании подобных конструкций одновременно с расчетом на прочность ведется расчет на устойчивость как отдельных узлов так и системы в целом.
Каковы условия и причины, при которых возможна потеря устойчивости системы?
В мире до сих пор нет четкого представления о причинах потери устойчивости конструкций. Этот вопрос остается объектом изучения как отдельных ученых так и целого ряда научных школ.
Считается, что нарушение устойчивости не является следствием каких- либо неправильностей конструкции (например, овальности цилиндров) или неоднородности материала и подобных причин, и исключительно следствием невозможности длительного существования системы данной геометрической формы при данных значениях геометрических и механических параметров. Так, например, поставленный на вершину прямой конус будет неустойчив, если бы даже его геометрическая форма была совершенна, материал абсолютно однороден, а ось вертикальна. Равным образом тонкостенный цилиндр или сфера станут неустойчивыми, хоть бы их форма была совершенна и материал абсолютно однороден, когда внешнее давление на них достигнет определенного значения и они неизбежно деформируются и примут новую форму.
При этом значение напряжений, действующих в стенках оболочек в случае действия внутреннего и наружного давлений получаются одинаковыми значения напряжений, так как в обоих случаях напряжения вычисляются по одним и тем же формулам, и различаются только знаками. Если, например, под действием внутреннего давления Рвн в стенках сосуда возникают напряжения растяжения, то при действии на этот сосуд наружного давления Рнар в его стенках возникнут сжимающие напряжения, равные по абсолютной величине.
Однако равенство величин растягивающих и сжимающих напряжений, возникающих при действии на сосуд равных, но противоположных по направлению нагрузок, не дает еще право сделать вывод, что сосуд будет одинаково работоспособен в обоих случаях, хотя бы он был изготовлен из материала, равнопрочного при растяжении и сжатии. В качестве одной из основных причин потери устойчивости считается появление напряжений сжатия в тонкостенных сосудах, зачастую меньших, чем допускаемые напряжения сжатия или растяжения.
Наименьшие напряжения сжатия, при которых оболочка уже теряет устойчивость формы, называют критическими. Нагрузки (силы, моменты, давления), вызывающие критическое напряжение, также называют критическими. Связь между критическими нагрузками и напряжениями выражаются теми же формами, что при расчете прочности, например
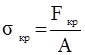 , (4.1)
, (4.1)
или
 . (4.2)
. (4.2)
Расчет устойчивости зачастую сводится к проверке оболочки на устойчивость при толщине стенки, определенной в расчете на прочность. Если толщина стенки окажется недостаточной для обеспечения устойчивости, необходимо усиление оболочки дополнительными элементами (кольцами жесткости), повышающими ее сопротивление потере устойчивости согласно рисунку 4.1, или заново рассчитать толщину стенки, исходя уже из требований обеспечения устойчивости.

а б
Рисунок 4.1 – Корпус аппарата: а – с «рубашкой»; б–с кольцами жесткости
Таким образом все расчеты устойчивости заключаются в определении действующего напряжения сжатия, критического напряжения (нагрузки, давления) и в обеспечении условий устойчивости. Например, при действии наружного давления
 , (4.3)
, (4.3)
или
 , (4.4)
, (4.4)
где  – критические значения, соответственно, давления и напряжения, МПа;
– критические значения, соответственно, давления и напряжения, МПа;
 – действительные (рабочие) значения этих величин, МПа
– действительные (рабочие) значения этих величин, МПа
n – коэффициент запаса устойчивости.
В нефтеперерабатывающей и нефтехимической промышленности появление сжимающих напряжений в аппаратах встречается очень часто. Например, это происходит когда аппараты нагружены осевой сжимающей силой F (под действием собственной массы), внешним давлением Рнар (в случае аппарата с рубашкой), находятся под вакуумом, или на них действует изгибающий момент М. При одновременном их действии условие устойчивости (4.3) согласно ГОСТ 14249 – 94 имеет вид
 , (4.5)
, (4.5)
где [F] – допускаемое значение осевой сжимающей силы, МПа;
[М]– допускаемый изгибающий момент, МНм;
 и
и  – соответственно расчетное и допускаемое наружные давления, МПа.
– соответственно расчетное и допускаемое наружные давления, МПа.
При отсутствии наружного давления, осевой сжимающей силы или изгибающего момента в выражении (4.5) принимают соответственно  , F= 0 или М= 0.
, F= 0 или М= 0.
Допускаемые наружное давление  ,осевую сжимающую силу [F] и изгибающий момент [М]следует определять по формулам:
,осевую сжимающую силу [F] и изгибающий момент [М]следует определять по формулам:
 , (4.6)
, (4.6)
 , (4.7)
, (4.7)
 , (4.8)
, (4.8)
где  ,
,  – допускаемое наружное давление соответственно из условий прочности и устойчивости в пределах упругости; МПа
– допускаемое наружное давление соответственно из условий прочности и устойчивости в пределах упругости; МПа
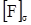 ,
,  – допускаемая осевая сжимающая сила соответственно из условий прочности и устойчивости в пределах упругости, МН;
– допускаемая осевая сжимающая сила соответственно из условий прочности и устойчивости в пределах упругости, МН;
 ,
,  – допускаемый изгибающий момент соответственно из условий прочности и устойчивости в пределах упругости, МHм.
– допускаемый изгибающий момент соответственно из условий прочности и устойчивости в пределах упругости, МHм.
При проверке устойчивости обечаек вертикальных сосудов и аппаратов за расчетное принимают сечение в зоне опор. Если толщина стенки обечайки по высоте аппарата меняется, то проверку устойчивости обечайки производят в каждом месте изменения толщины.
Выбор необходимой и достаточной величины запаса устойчивости, входящий в формулу (4.3) представляет собой весьма ответственное дело. Слишком малая величина запаса устойчивости nсделает сосуд ненадежным к работе, слишком большая – тяжелым и дорогим.
На величину запаса устойчивости влияют правильность формы и симметричность нагрузки, зависящие от технологии изготовления и положения сосуда в пространстве, а также экономические соображения. В зависимости от способа изготовления отклонение формы сечения сосуда от круглой может быть различным.
Нужно учитывать возможность существования невидимой глазу прочностной асимметрии, которая может быть в сосуде вследствие остаточных термических напряжений, например, вблизи сварных швов, и может снизить величину критического давления.
Асимметричность нагрузки увеличивается при отклонении геометрической оси цилиндра от вертикали, так как в стенках сосуда возникают дополнительные изгибные напряжения от веса частей сосуда. Понятно, что чем больше геометрическая и силовая асимметрия, тем больше должен быть запас устойчивости и тем меньше допускаемое давление. Сосуды, нагруженные внешним давлением, могут изготавливаться не только из дешевых углеродистых сталей, но и из дорогих и дефицитных высоколегированных сталей, цветных металлов и их сплавов. В этих случаях экономические соображения требуют, чтобы величина запаса устойчивости не была преувеличенной.
В разные годы величина запаса устойчивости менялась. Например, в сороковые – шестидесятые годы двадцатого века величина n была равна 5 – 6 для цилиндров обычной точности из дорогих металлов, при условии тщательного изготовления 3 – 4. Для цилиндров из углеродистой стали обычной точности изготовления 6 – 9. А значений ниже 3 – 4 вообще не рекомендовалось допускать. С развитием более точных методов и расчетов на устойчивость величина n снизилась и по ГОСТ 14249 – 94 равна 1,8 – для условий испытания и монтажа, и 2,4 – для рабочих условий.
Дата добавления: 2015-07-11; просмотров: 142 | Нарушение авторских прав