Расчет цилиндрических оболочек при общей потере устойчивости

При общей потере устойчивости оболочка рассматривается как длинный стержень, при этом

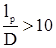, (4.13)

где l_p – расчетная длина обечайки, м;

D – диаметр обечайки, м; как это показано на рисунке 4.6

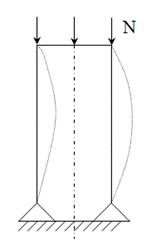
Рисунок 4.6 – Длинный стержень

Расчет оболочек на устойчивость при общей потере устойчивости производится как для длинных стержней. При этом допускаемое осевое сжимающее усилие определяется по формуле (4.14)

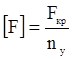, (4.14)

где F_кр – критическая нагрузка, МН;

n_у – коэффициент запаса устойчивости.

Критическая нагрузка F_кр определяется по известной формуле Эйлера

. (4.15)

Для длинной тонкостенной оболочки, ввиду малости отношения толщины стенки к диаметру, момент инерции сечения может быть выражен

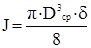, (4.16)

где – минимальная толщина стенки, сохраняющая к концу срока службы аппарата.

Подставив (4.16) в (4.15), и выразив 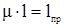, получим

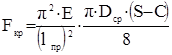, (4.17)

где .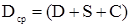

И окончательно получим

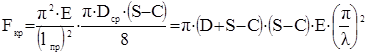, (4.18)

где – гибкость оболочки.

Допускаемое напряжение из условия общей потери устойчивости определяется по формуле (4.19)

[F]_y1 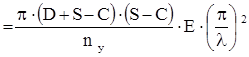, (4.19)

где l_пр – приведенная расчетная длина центрально сжатых элементов, м.

Дата добавления: 2015-07-11