Расчет цилиндрических оболочек при местной потери устойчивости.

Местная (локальная) потеря устойчивости наблюдается когда происходит волнообразное выпучивание стенки, при этом () как это показано на рисунке 4.7.

Рисунок 4.7 – Местная потеря устойчивости

При местной потери устойчивости критические напряжения определяются по классической формуле Лоренца-Тимошенко

, (4.20)

или при m = 0,3

. (4.21)

Это верхнее критическое напряжение. Как показали многочисленные эксперименты, проведенные целым рядом исследователей, формула (4.21) критических напряжений для идеальных оболочек дает значения, существенно большие, чем наблюдаемые на опыте. Даже для оболочек, изготовленных с большей тщательностью точением на токарном станке, значения критических напряжений оказываются в два-три раза меньше по сравнению с данными теории для идеальных оболочек. Величина коэффициента устойчивости, при котором происходит разрушение составляет от 0,15 до 0,3 вместо 0,605. Следует отметить, что осевое сжатие является самым показательным с точки зрения несоответствия теоретических решений большинству экспериментов.

Экспериментальные значения F _кр отличались от теоретических на 10-90%. Поэтому расчет вели по нижней критической нагрузке. Для нее было предложено много различных формул как эмпирических, так и теоретических. В общем виде зависимость для 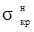имеет вид

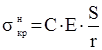, (4.22)

где С – отношение критического напряжения к верхнему .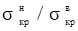

Для С получено много значений от 0,07 до 0,948. Например, русским ученым Алексеевым получена такая формула для С

. (4.23)

Этот результат интересен тем, что величина С зависит от относительной толщины оболочек, что качественно соответствует экспериментам. Тогда формула (4.22) запишется

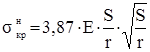. (4.24)

Перейдя от напряжений к усилиям, и проделав ряд преобразований, учитывая, что 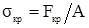, где – площадь поперечного сечения оболочки, м², получим формулу для допускаемого осевого сжимающего усилия из условия местной устойчивости.

, (4.25)

где – площадь поперечного сечения оболочки, м²

Допускаемое осевое сжимающее усилие рассчитывают по формуле (4.7), где допускаемое осевое сжимающее усилие из условия прочности определяется по формуле (4.26)

, (4.26)

а допускаемое осевое сжимающее усилие из условия устойчивости в пределах упругости определяется по формулам (4.27) и (4.28)

, (4.27)

если и

, (4.28)

если .

Разрушение сжимающего элемента может быть следствием

– потери устойчивости;

– потери прочности;

– потери того и другого.

То есть существует какая-то промежуточная область, когда разрушение является следствием и частичной потери устойчивости и накоплением повреждений в материале элемента (частичной потери прочности). В этом случае необходимо определить какую-то среднюю величину допускаемой осевой сжимающей силы, которая находится как гармоничное по формуле (4.29)

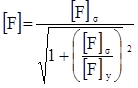. (4.29)

Данное уравнение является простейшей интерполяцией с правильными асимптотами между двумя крайними случаями: потерей устойчивости в пластической области или упругой.

Цилиндрические оболочки, применяемые в нефтепереработке и нефтехимии могут быть как с отверстиями так и без них. Основные расчетные формулы, полученные выше применяются для гладких оболочек (без отверстий), однако, кроме этого, изучаются особенности потери устойчивости цилиндрических оболочек с отверстиями, которые могут иметь различную форму и размеры и располагаться в различных сечениях. Поэтому ниже в подразделе 3.2 будут приведены небольшие теоретические выводы по данной проблеме.

Кроме этого, различают оболочки нагруженные равномерно распределенными осевыми силами, а также неравномерно распределенными по окружности локальными силами. Некоторые аспекты данной проблемы приведены в подразделе 4.2.3

Дата добавления: 2015-07-11