Расчет длинных оболочек под действием наружного давления

В этом случае влиянием краевых условий можно пренебречь, а задача сводится к расчету кольца единичной длины, нагруженного равномерно распределенным наружным давлением.

Если вырезать элемент из кольца, приложить нагрузки и внутренние силовые факторы и рассмотреть условия равновесия его до деформации и после, получим выражение для q

, (4.36)

где n – число полных волн, образующихся при выпучивании по окружности кольца,

– жесткость кольца, МНм²;

J – момент инерции сечении кольца, м⁴;

E – модуль упругости первого рода, МПа.

При n =1 задача теряет смысл. Из соотношения (4.36) следует, что минимальное значение q, соответствующие критической нагрузке, будет при n = 2, тогда из (4.36) получим

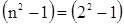, (4.37)

. (4.38)

Следовательно, выпучивание кольца произойдет по двум волнам.

Результаты, полученные для кольца, без труда распространяются на длинные цилиндрические оболочки, нагруженные внешним давлением. В данном случае q = PI, а жесткость оболочки на изгиб равна

. (4.39)

Таким образом

, (4.40)

. (4.41)

Поскольку окружное сжимающее напряжение в оболочке, нагруженное равномерным внешним давлением, равно

, (4.42)

то критическое окружное сжимающие напряжение равно

. (4.43)

Дата добавления: 2015-07-11