Пример 3.

Построить функцию распределения долговечности до разрушения детали из алюминиевого сплава при нерегулярном нагружении, заданном распределением амплитуд спектра эксплуатационной нагрузки в соответствии с законом Рэлея:

,

где параметр s =30 МПа, максимальная амплитуда 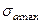=100 МПа. Эта функция представлена на рисунке 15.53.

Пусть медианная кривая усталости детали при симметричном цикле имеет следующий вид:

(15.191)

где параметры и A равны соответственно 50 и 1000 МПа.

Для расчета медианы долговечности достаточно этих данных. Для построения всей функции распределения необходимо располагать также параметрами квантильных кривых усталости, то есть кривых усталости, построенных по параметру вероятности разрушения. Так как построение семейства таких кривых требует большого числа экспериментальных данных, что не всегда возможно при длительных усталостных испытаниях, в первом приближении для вычисления квантили долговечности при регулярном нагружении воспользуемся известным приближением функции распределения логарифма долговечности на основании нормального закона:

,

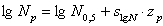где lg N _0.5 определяется по уравнению медианной кривой усталости, а среднее квадратическое отклонение примем постоянным и равным 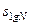=0,15, что в первом приближении подтверждается большим числом экспериментальных данных усталостных испытаний деталей, элементов авиаконструкций и конструктивно подобных образцов из алюминиевых сплавов; - квантиль нормированного нормального закона распределения, соответствующая вероятности p. Тогда уравнение (15.190) для определения функции распределения ресурса при нерегулярном нагружении примет следующий вид:

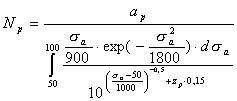(15.192)

.

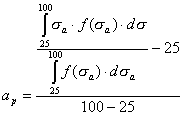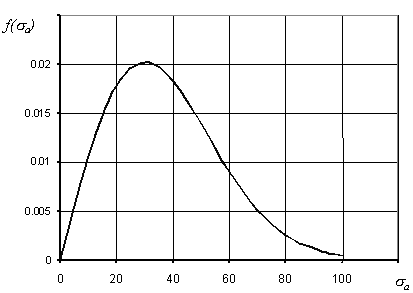
Рис. 15.53. Функция плотности распределения амплитуд спектра эксплуатационной нагрузки

Проведенный расчет функции распределения долговечности при нерегулярном переменном нагружении представлен в таблице 15.2.

В таблице 15.2 для примера представлен также расчет логарифма долговечности при той же нагруженности, но по степенному уравнению кривой усталости с нулевым значением предела неограниченной выносливости:

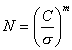(15.193)

где параметр m =4, С =10^3,5. На рисунке 15.54 построены графики этих функций на нормальной вероятностной бумаге.

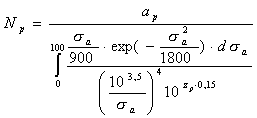(15.194)

.

Отметим, что при расчете по уравнению (15.192) значение 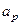составило 0,283, а при расчете по уравнению (15.194) – 0,373. Кривые усталости для двух рассматриваемых в примере вариантов представлены на рисунке 15.55.

Таблица 15.2. Расчет функции распределения логарифма долговечности при нерегулярном нагружении

P	0.01	0.05	0.1	0.2	0.3	0.5	0.7	0.8	0.9	0.95	0.99
(15.192)	5.74	5.842	5.896	5.962	6.01	6.089	6.167	6.215	6.281	6.335	6.437
(15.194)	6.45	6.552	6.607	6.673	6.72	6.799	6.878	6.925	6.991	7.046	7.148

Основой расчета долговечности при нерегулярной нагрузке, как видно из рассмотренных выше примеров, является обоснование уравнения кривой усталости детали при регулярном нагружении. Наиболее надежным способом обоснования такой кривой усталости являются прямые усталостные испытания натурных деталей с последующей статистической обработкой их результатов. Как показывают расчеты для достижения достаточной точности оценивания характеристик усталостных свойств при усталостных испытаниях требуется порядка 30-50 объектов, что в условиях натурных испытаний является практически нереальным.

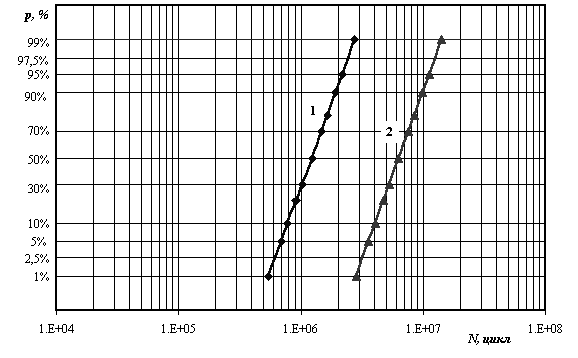
Рис. 15.54. Расчетные функции распределения логарифма долговечности при нерегулярном нагружении

по уравнениям (15.192) (линия 1), (15.194) (линия 2)

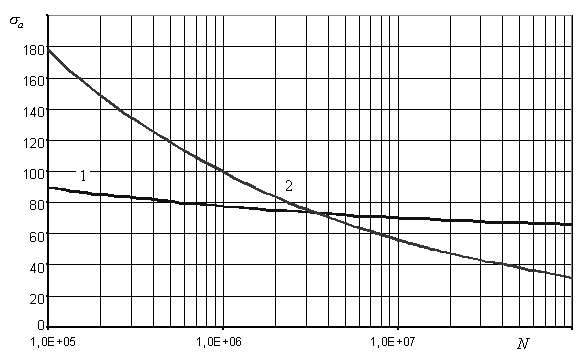
Рис. 15.55. Кривые усталости детали при симметричном нагружении, построенные

по уравнениям (15.192) (кривая 1), (15.194) (кривая 2)

В практике авиационных расчетных подразделений сложился комбинированный способ обоснования кривой усталости натурных деталей, суть которого заключается в выявлении опасных зон элемента конструкции (ресурсоограничивающих зон), изучении конструктивных и технологических особенностей этих зон, их нагруженности и последующего создания моделей или так называемых конструктивно-подобных образцов, которые по основным конструктивным, масштабным и другим характеристикам были бы подобны деталям в опасных зонах элемента конструкции. Испытаниям подвергаются в дальнейшем эти модельные образцы, стоимость которых ненамного выше обычных лабораторных образцов. В основном в качестве таких моделей в авиации используются для целей обоснования кривой усталости плоские образцы с отверстием, моделирующие масштабный эффект и концентрацию напряжений натурной детали. Полученная таким образом кривая усталости лишь приближенно отражает действительную кривую усталости элемента конструкции. Для уточнения такой кривой усталости по возможности следует проводить хотя бы единичные испытания натурной детали на одном уровне регулярной нагрузки. При этом в первом приближении можно считать, что показатель степени кривой усталости натурной детали равен показателю степени кривой усталости модельных образцов (то есть кривые усталости являются эквидистантными), но значение второго параметра уравнения кривой усталости, определяющего сдвиг одной кривой относительно другой, может быть уточнено.

Опыт показывает, что гипотеза линейного суммирования позволяет достаточно точно определить долговечность, если все амплитуды превышают предел выносливости материала детали и отсутствуют резкие всплески напряжений. Кроме того, опытами показано, что линейное суммирование повреждений подтверждается при монотонном увеличении амплитуд с ростом числа циклов, и действует иной закон накопления повреждений, если сначала приложить циклическую нагрузку с амплитудами, близкими к пределу текучести материала.

Таким образом, на долговечность существенно влияет история нагружения. Экспериментально установлено, что образец, нагруженный сначала циклическими напряжениями, меньшими предела выносливости, при дальнейшем повышении амплитуд малыми порциями показывает большую долговечность, чем исходная. В то же время предварительно перенапряжение образца циклическими напряжениями выше предела выносливости приводит к противоположным результатам. Однако вредное влияние перенапряжения начинает сказываться только после некоторого предельного числа циклов перенапряжения, зависящего от величины этих напряжений.

При случайном изменении амплитуд напряжений явления усталостного упрочнения и разупрочнения будут чередоваться и отчасти нивелироваться, что оправдывает в известной степени применение гипотезы накопления повреждений к таким нерегулярным режимам изменения напряжений.

Любой теоретический подход к проблеме долговечности конструкции при нерегулярном изменении напряжений требует экспериментальной проверки теоретических методов.

В настоящее время исследования проводятся по двум основным направлениям. Одно из них состоит в испытании непосредственно конструкций по программе нагружения, возможно ближе подходящей к экспериментально определенному спектру нагрузок.

Другое направление исследования состоит в испытании лабораторных образцов по различным ступенчатым программам циклического нагружения, в которых изменяется последовательность чередования нагрузок разной интенсивности с различным количеством циклов их действия. Исследуется влияние параметров нагрузки на долговечность образцов и полученные закономерности используются для оценки долговечности конструкций.

Вопросы для самопроверки

- Что называется циклом напряжений? Перечислить все характеристики цикла и указать зависимость между ними.

- Какой из различных по форме циклов напряжений самый неблагоприятный для работы детали?

- Что называется усталостным разрушением и каковы его причины?

- Что называется пределом выносливости материала?

- Каково соотношение пределов выносливости при различных циклах нагружения?

- Влияние размеров, формы, шероховатости на величину предела выносливости.

- Концентраторы напряжений. Как они влияют на предел выносливости?

- Что такое концентрация напряжений и в чём причина их возникновения?

- Что такое теоретический коэффициент концентрации напряжений и что такое эффективный коэффициент концентрации напряжений? От чего зависит величина того и другого?

- Каково влияние абсолютных размеров детали на её прочность? На предел выносливости?

- Как производится проверочный расчёт на прочность (определение фактического запаса) при переменных напряжениях?

- По какой формуле определяется коэффициент асимметрии цикла.

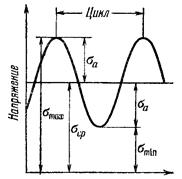
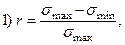
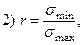
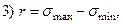
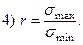
- Какова величина коэффициента асимметрии цикла, если цикл симметричен?

1) ;

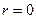2) ;

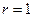3) ;

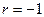4) .

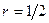- По какой формуле определяется коэффициент асимметрии цикла:

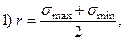
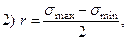
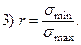
- По какой формуле определяется амплитуда цикла:

1)

2)

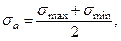
3)

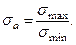
- Основной фактор, влияющий на величину предела выносливости?

1. Вес конструкции.

2. Концентрация напряжений.

3. Внешняя окружающая среда.

4. Абсолютные размеры деталей.

- Что называется пределом усталости?

1. Это максимальное напряжение, при котором материал не разрушается.

2. Это наибольшее напряжение, при котором материал не разрушается при любом числе циклов.

3. Это напряжение, при котором материал способен выдержать 10⁸ циклов.

4. Это наибольшее количество циклов, которое выдерживает материал, не разрушаясь.

- Почему концентрация напряжений менее опасна для пластических материалов, чем для хрупких?

1. Потому, что для уменьшения концентрации напряжений можно изменить форму деталей.

2. Для пластических материалов для снижения высоких местных напряжений у трещин применяется рассверливание концов этих трещин.

3.В пластических материалах увеличение нагрузки сопровождается перераспределением напряжений.

4. При статическом нагружении деталей из пластичных материалов концентрация напряжений практически не оказывает влияние на прочность и не учитывается при расчетах.

- Понятие «цикла» при напряжениях, циклически изменяющихся во времени.

1. Время одного периода.

2. Совокупность значений напряжений за время одного периода.

3. Период времени, когда напряжения принимают значения от до _.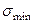

4. Время, в течении которого происходит процесс усталостного разрушения.

- Понятие термина «усталость».

1. Это процесс постепенного накопления повреждений материала при действии переменных напряжений, приводящий к образованию трещин и разрушению.

2. Это свойство материалов сопротивляться действию внешней нагрузки, которая является переменной.

3. Это предельное напряжение, при котором происходит разрушение.

4. Это процесс, при котором происходит разрушение и образование трещин.

- Предел выносливости характеризует:

1. число циклов, которое выдерживает материал;

2. прочность материала при циклическом нагружении;

3. характер усталостного нагружения.

- Самый опасный цикл нагружений симметричный.

1. да;

2. нет;

3. пульсационный.

- От характера изменения напряжений внутри цикла предел усталости не зависит.

1. незначительно;

2. да;

3. нет.

- Предел выносливости зависит от:

1. концентрации напряжений;

2. формы и размеров детали;

3. вида цикла и его параметров, геометрической формы и размеров, состояния поверхности и концентраторов напряжений.

- Главными параметрами циклов являются:

1. , ;

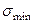2. , ;

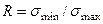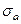3. .

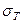- Какой цикл изменения напряжений является самым опасным:

1. асимметричный,

2. пульсационный,

3. симметричный.

- Что характеризует предел выносливости

1. прочность при изгибе;

2. максимальное напряжение цикла при базовом числе циклов нагружений;

3. напряжение при симметричном цикле нагружений.

Дата добавления: 2015-07-12