Молекула водорода

& Литература: [1], [7], [8], [6].

Рассмотрение молекулы водорода позволяет понять природу химических связей, реализуемых в молекулах и в конденсированных средах.

Подобно атому гелия молекула водорода содержит два электрона, и поэтому ее волновая функция должна иметь спиновой сомножитель
Y(s₁ s₂), аналогичный спиновой части волновой функции атома гелия
(см. (29.4) – (29.7)). Имеется три спиновых состояния с суммарным спином
s = 1 (параллельные спины ↑↑), описываемые симметричными функциями (29.4) – (29.6), и одно состояние со спином s = 0 (антипараллельные спины ↑↓), описываемое симметричной функцией (29.7). Соответственно, координатная часть Y(1, 2) волновой функции молекулы водорода должна быть симметричной в случае антипараллельных спинов и антисимметричной, если спины параллельны:

Y(1, 2) = Y_s(1, 2) = Y_↑↓(1, 2) (32.1)

Y(1, 2) = Y_a(1, 2) = Y_↑↑(1, 2) (32.2)

Цифры 1 и 2 в качестве аргументов функции обозначают координаты первого и второго электрона.

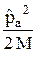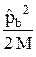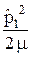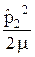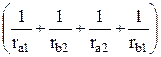Координатная часть волновой функции Y(1, 2) находится посредством решения стационарного уравнения Шредингера с таким гамильтонианом: = + + + – e²k + e²k 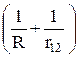. (32.3)

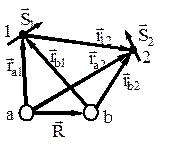Рис. 32.1

Здесь M – масса протона, m – масса электрона, k = 1 / (4 p e₀). Смысл остальных величин ясен из рисунка 32.1.

При решении задачи используют так называемое адиабатическое приближение, основанное на малости массы электрона m по сравнению с массой протона M.

На первом этапе теории адиабатического приближения в выражении (32.3) пренебрегают величиной

_ab = 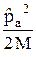+ 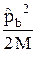(32.4)

и решают стационарное уравнение Шредингера с оставшейся частью
_R(1, 2) гамильтониана: _R(1, 2) Y_R(1, 2) = E(R) Y_R(1, 2). (32.5)

Физический смысл сделанного приближения заключается в пренебрежении движением ядер. Уравнение (32.5) описывает движение электронов в поле неподвижных ядер. Расстояние R между ядрами входит в (32.5) в качестве параметра.

В операторе _R(1, 2) целесообразно выделить следующие слагаемые:

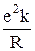_R(1, 2) = _a(1) + _b(2) + + , (32.6)

где _a(1) и _b(2) – гамильтонианы изолированных атомов водорода с ядрами a и b, а – оператор возмущения, описывающий взаимодействие электронов друг с другом и с «чужими» ядрами:

= e² k 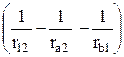. (32.7)

Тогда в нулевом приближении (» 0) получается уравнение Шредингера с разделяющимися переменными. В результате приходим к заключению, что энергия E⁰(R) рассматриваемой системы в нулевом приближении является суммой энергий изолированных атомов E_a и E_b и кулоновской энергии взаимодействия ядер: E⁰(R) = E_a + E_b + 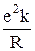. (32.8)

↑↓

Волновые функции, соответствующие значению E⁰(R), должны иметь вид линейных комбинаций, составленных из произведений Y-функций изолированных атомов. Причем эти комбинации должны быть симметричными или антисимметричными подобно тому, как это имело место в случае атома гелия (см. (29.13)):

↑↑

Y_R(1, 2) = N_±(R) {Y_a(1) Y_b(2) ±Y_a(2) Y_b(1)}. (32.9)

Здесь N_±(R) – нормирующий множитель, Знак «+» соответствует антипараллельной ориентации спинов ↑↓, а знак «–» – параллельной ↑↑ (см. (32.1)
и (32.2)).

↑↓

Каждому уровню (32.8) соответствуют два состояния (32.9). Возмущение (32.7) снимает это вырождение. Для нахождения поправок DE, определяющих положение подуровней, целесообразно воспользоваться соотношением (26.10), аналогично тому, как это делалось в случае атома гелия. Получим:

↑↑

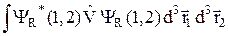DE = ÞDE = 2 N_±²(R) (Q ± A), (32.10)

где Q = 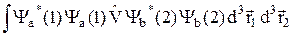– (32.11)

кулоновский интеграл, а

A = 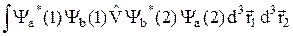– (32.12)

обменный интеграл.

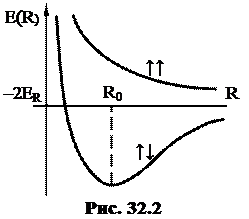Структура формул (32.11) и (32.12) такая же, как и (29.21) и (29.22) для атома гелия. Следовательно, аналогичен и смысл описываемых ими величин Q и A. Отличие – в несколько ином виде оператора возмущения, а также в том, что в (32.12) предполагается переход электронов от одного атома к другому и наоборот, а в (29.22) – переход электронов одного и того же атома из одного состояния в другое.

Складывая (32.8) и (32.10), получим энергию E(R) рассматриваемой системы при фиксированных расстояниях R между протонами. На рисунке 32.2 показан характер зависимости E(R) для обеих взаимных ориентаций электронных спинов.

При антипараллельной ориентации спинов энергия оказывается не только меньше из-за того, что A < 0, но и имеет минимум в точке R = R₀. Наличие этого минимума означает, что образуется связанная система с равновесным расстоянием R₀ между центрами двух атомов водорода. Говорят, что атомы соединяются в молекулу водорода посредством ковалентной связи. При параллельной ориентации спинов связанная система не образуется. Возникновение ковалентной связи обусловлено величиной A, входящей в формулу (32.10). Эта величина отражает обменное взаимодействие, которое, оставаясь электромагнитным по своей природе, существенно зависит от взаимной ориентации спинов электронов.

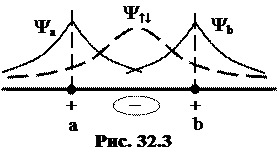Парадоксальное на первый взгляд электрическое притяжение между нейтральными атомами водорода, проявляющееся при ковалентной связи, становится естественным, если проанализировать распределение электрического заряда в состояниях, описываемых формулой (32.9).

На рисунке 32.3 сплошными линиями изображены атомарные функции Y_a и Y_b в 1s-состояниях, а пунктиром – симметричная молекулярная функция Y_↑↓, определяемя формулой (32.9). Благодаря знаку «+» в (32.9), функция Y_↑↓ имеет максимум посредине между ядрами a и b. Здесь плотность отрицательных зарядов оказывается максимальной. Это и приводит к стягиванию положительных ядер a и b.

Для параллельной ориентации спинов электронов в формуле (32.9) нужно брать знак «–». Тогда возникает ситуация, изображенная на рис. 32.4. Молекулярная функция Y_↑↑ равна нулю посредине между ядрами. Отрицательные заряды главным образом оказываются локализованными с внешней стороны ядер. Они удаляют ядра друг от друга.

Второй этап теории адиабатического приближения заключается в анализе движения ядер, для чего следует учесть отброшенную на первом этапе часть гамильтониана (32.4) при решении стационарного уравнения Шредингера:

{ _R(1, 2) + _ab(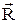)} Y(1, 2, 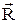) = E Y(1, 2, 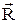). (32.13)

Функция Y(1, 2, 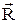), удовлетворяющая уравнению (32.13), описывает движение и электронов, и ядер. Ее представляют в виде произведения:

Y(1, 2, 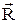) = Y_R(1, 2) Y(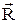), (18.14)

где Y_R(1, 2) – найденная на первом этапе функция (32.9), описывающая движение электронов в поле неподвижных ядер. Подставляя (32.4) и (32.5) в (32.13), можно приближенно (с учетом m << M) получить уравнение:

{ _ab(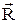) + E(R)} Y(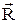)» E Y(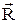). (32.15)

Оно описывает движение ядер в поле, создаваемом электронной подсистемой. E(R) играет роль потенциальной функции, характеризующей это поле.

Так в теории адиабатического приближения удается свести задачу к двум более простым: о движении электронной и о движении ядерной подсистем. Теория адиабатического приближения используется для молекул и конденсированных сред. Во всех случаях успех достигается благодаря условию m << M.

Решение стационарного уравнения Шредингера (32.15) для сферически симметричной потенциальной ямы, изображенной на рисунке 32.2, приводит, в частности, к следующему результату. Энергия E молекулы водорода складывается из трех слагаемых:

E = E_Эл + E_Вр + E_К. (32.16)

E_Эл = E(R₀) – энергия, соответствующая минимуму функции E(R), изображенной на рисунке 32.2. E_К – энергия колебательного движения молекулы, при котором периодически изменяются расстояния между ядрами. E_Вр – энергия вращательного движения молекулы как ротатора.

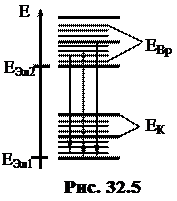Оценки порядка величин слагаемых в формуле (32.16) приводят к таким соотношениям:

» » .

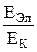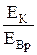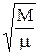По этой причине энергетический спектр молекулы водорода (и других молекул) имеет вид, показанный на рисунке 32.5.

Малое расстояние между вращательными уровнями обуславливает полосатый спектр молекул. На рисунке 32.4 стрелками отмечены переходы, принадлежащие одной из полос излучения.

? Контрольные вопросы

1. По какому плану решается задача о молекуле водорода.

2. Запишите гамильтониан молекулы водорода. Поясните смысл каждого слагаемого.

3. На чем основано и в чем заключается адиабатическое приближение?

4. Расскажите о нахождении волновой функции электронной подсистемы молекулы водорода.

5. Расскажите об энергии электронной подсистемы молекулы водорода.

6. Почему связанные состояния атомов возникают только при антипараллельной ориентации спинов.

7. Расскажите, как решается задача о молекуле водорода на втором этапе теории адиабатического приближения.

8. Получите формулу (32.15).

9. Расскажите об энергетическом спектре молекулы водорода.

Дата добавления: 2015-07-11