Решение. Формула энтропии H(x)=−∑ n i=1 p(i)log 2 p(i) , где n - число состояний системы

1.

2.

Формула энтропии H(x)=−∑ n i=1 p(i)log 2 p(i), где n - число состояний системы, p(i) - вероятность нахождения системы в i - состоянии

- - - =1,53 бит

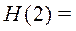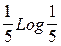- - - =1,500 бит

?? Определить среднее количество информации приходящейся на один символ сообщения 01001000101001, при условии, что источник эргодический, а последовательность – типичная.

Решение:

01 00 10 00 10 10 01

Источник – эргодический Последовательность – типичная Всего 14 символов, 0-9 и 1-5

Формула энтропии H(x)=−∑ n i=1 p(i)log 2 p(i), где n - число состояний системы, p(i) - вероятность нахождения системы в i - состоянии

17. Информация передается при помощи частотно-модулированных сигналов, рабочая частота F которых изменяется с равной вероятностью в пределах от F1=10МГц до F2=50МГц. Определить энтропию значения частоты, если точность измерения частоты DF=2кГц.

Решение:

Так как точность измерений составляет DF=2кГц, то мы имеем дело с числом равновероятных исходов. p(i)=1/ n

можно энтропию для равновероятных событий использовать: H(x)=log n

Поэтому энтропия частоты будет определяться:

Измерительное устройство регистрирует временные интервалы, распределенные случайным образом в пределах от 100 до 500мс. Как изменится энтропия случайной величины при изменении точности измерения с 1мс до 1мкс?

Решение:

При точности измерения 1мс случайная величина принимает (500-100)/1=400равновероятных значений, а значит ее энтропия: H(x)=log n

А при точности измерения 1мкс случайная величина принимает (500-100)/0.001=400000равновероятных значений, а значит ее энтропия:

.

Значит, энтропия случайной величины увеличится примерно на 10 бит.

19. Элементы алфавитов X и У статистически связаны. Известно, что Н(Х)=8 бит, Н(Y)=12 бит. В каких пределах меняется условная энтропия H(Y|X) при изменении H(X|Y) в максимально возможных пределах?

Решение:

Из свойств энтропии источников информации следует, что:

.

Условная энтропия может изменяться: , поэтому значения , которые она будет принимать при изменении , можно определить:

.

При минимальном значении : .

При максимальном значении : .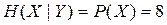

20. В результате полной дезорганизации управления m самолетов летят
произвольными курсами. Управление восстановлено, и все самолеты взяли общий курс со среднеквадратической ошибкой отклонения от курса s=З°. Найти изменение энтропии, считая, что в первом случае имело место равномерное распределение вероятностей углов, а во втором случае - нормальное.

Решение:

Рассмотрим каждый самолет, как случайную величину. Так, как в первом случае имеет место равномерное распределение вероятностей углов, а у нас углы изменяются от 0 до 360^о, то функция распределения вероятности для одного самолета равна f(x)=1/360.

Для равновероятных случайных величин:

.

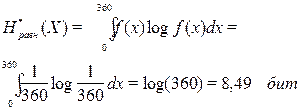Для второго случая считаем по формуле:

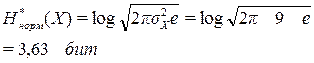
Таким образом, изменение энтропии составит:

Дата добавления: 2015-10-21