Формула Шеннона

Рассмотрим статический опыт, имеющий k равновероятных исходов. Таблица вероятностей такого опыта имеет следующий вид.

Исходы опыта	А1	А2	А3	…	Аk
Вероятности	1/k	1/k	1/k	…	1/k

Общая неопределенность этого опыта может быть оценена величиной log k. Каждый отдельный исход, имеющий вероятность 1/k, вносит неопределенность, равную .

В том случае, если исходы имеют различную вероятность, (см. таблицу вероятностей),

Исходы опыта	А1	А2	А3
Вероятности	1/2	1/3	1/6

то исходы А₁, А₂, А₃ вносят соответственно неопределенность равную:

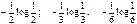. В случае независимости исходов общая неопределенность опыта будет равна: .

Обобщая рассмотрение вышеизложенного можно для опыта α с таблицей вероятностей

Исходы опыта	А1	А2	…	Аk
Вероятности	p (А1)	p (А2)	…	p (Аk)

сделать оценку в виде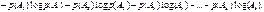

В результате для опыта α мы получаем число, являющееся количественной мерой неопределенности опыта. Эта величина называется энтропией, а формула Шеннона для расчета энтропии имеет вид: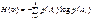

_______________

Дата добавления: 2015-10-21