Код Шеннона-Фано

Идея использования неравенства H < log n для построения экономичного кода очень эффективно используется в кодах, которые впервые предложили в 1948 – 1949 гг. Р. Фано и К. Шеннон.

Предположим, что алфавит содержит n букв. Расположим буквы алфавита в один столбик в порядке убывания вероятностей. Затем разобьем их на две группы – верхнюю и нижнюю. Для букв первой группы в качестве первой цифры кодового обозначения используем 1, а для букв второй группы – цифру 0. Далее, каждую из двух полученных групп снова разделим на две части с возможно более близкой суммарной вероятностью. В качестве второй цифры кодового обозначения используются цифры 1 и 0 в зависимости от того, принадлежит ли буква к первой или второй из этих подгрупп. Затем каждая из содержащих более одной буквы групп снова делится на две части и т.д. Процесс повторяется до тех пор, пока каждая из разделенных групп будет содержать по одной букве.

Рассмотрим несложный принцип кодирования по методу Шеннона–Фано. Допустим, что алфавит содержит всего шесть букв, вероятности которых в порядке убывания равны 0,4; 0,2; 0,2; 0,1; 0,05; 0,05 (см. таблицу).

№ буквы	Вероятность	Группы	Кодовое обозначение
	0,4 0,2 0,2 0,1 0,05 0,05	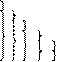2 2 1 2 1 2 2

Основной принцип, положенный в основу кодирования по методу Шеннона-Фано заключается в том, что при выборе каждой цифры кодового обозначения стараются, чтобы содержащаяся в ней информация была наибольшей. Разумеется, количество цифр в различных обозначениях будет неодинаковым, то есть код Шеннона-Фано является неравномерным. Буквы, имеющие большую вероятность, получают более короткие обозначения, чем соответствующие маловероятные буквы. В результате, хотя некоторые кодовые обозначения здесь и могут иметь весьма значительную длину, среднее значение длины такого обозначения значительно уменьшается.

Дата добавления: 2015-10-21