Свойства энтропии

1. Энтропия не может принимать отрицательных значений:

.

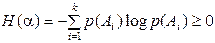Это несложно доказать, т.к. 0 £р(А)£ 1, а в этом интервале функция

log p(A) всегда отрицательна.

2. Энтропия H(α) равна 0 только в том случае, когда одна из вероятностей р(А₁), р(А₂),… р(А_k) равна единице, а все остальное равно 0.

Это становится очевидным, так как р(А₁) + р(А₂) + … + р(А_k) = 1, и согласно физическому смыслу, нулевое значение энтропии возможно только в том случае, когда опыт не содержит никакой неопределенности.

3. Среди всех опытов, имеющих k исходов, наиболее неопределенным является опыт с таблицей вероятности (см.таблицу),

Исходы опыта	А1	А2	…	Аk
Вероятности	1/k	1/k	…	1/k

который принято обозначать за опыт α₀. В этом случае предсказать исход опыта труднее всего. Этому отвечает то обстоятельство, что опыт α₀ имеет наибольшую энтропию. Данное свойство довольно часто используется, а его доказательство очень громоздкое, поэтому ограничивается утверждением: если α – произвольный опыт, имеющий k исхода (А₁, А₂, А_3,,…, А_k,), то

_______________

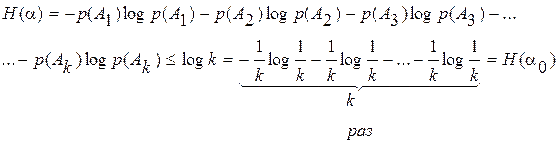
Дата добавления: 2015-10-21