Расчет прочности наклонных сечений

Расчет железобетонных элементов по наклонным сечениям, согласно п.3.29 [5], должен производиться для обеспечения прочности:

– на действие поперечной силы по наклонной полосе между наклонными трещинами;

– на действие поперечной силы по наклонной трещине;

– на действие изгибающего момента по наклонной трещине.

Проверим прочность балки в сечениях слева от первой промежуточной опоры, где действует наибольшая поперечная сила и справа от нее – в целях облегчения конструкции и экономии материала.

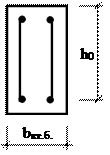
Следует иметь в виду, что в опорных сечениях полка расположена в растянутой зоне бетона и поэтому коэффициент j_f = 0, т.е. сечение рассматривается как прямоугольное.

Сечение слева от первой промежуточной опоры:

Расчет на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами производится согласно п. 3.30 [5].

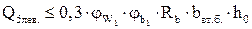
Коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле:

Рис. 12

α=Es/Eb

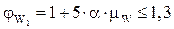
Для определения коэффициента 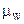необходимо предварительно задаться шагом хомутов в зависимости от высоты сечения второстепенной балки: если она более 450 мм, то шаг хомутов принимается равным 1/3 от высоты второстепенной балки, но не более 500 мм.

Принимаем шаг хомутов 150 мм, а их диаметр из условия свариваемости равным ≥1/3 диаметра продольных стержней, т.е. 10 мм.

Тогда μw=Asw/b*s=0.789/20*15=0.00263

φw1≈1

Коэффициент 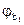определится по формуле:

,

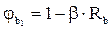φb1=1-0.01*15.3=0.845

где 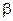=0,01 для тяжелого бетона.

Таким образом, имеем:

0.3*1*0.845*15.3МПа*200мм*350мм=271,49 кН ≥ 124.81 кН

Условие прочности выполняется.

Проведем проверку прочности наклонных сечений по поперечной силе. Как показывают опыты, наклонные трещины могут развиваться как непосредственно у опоры, так и на некотором удалении от нее.

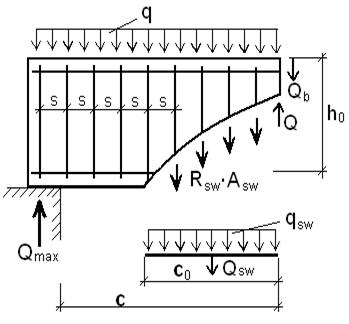В первом случае с=с₀, а во втором – с > с₀.

Определяем значения:

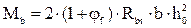
Как говорилось ранее, коэффициент 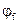=0. Тогда

Mb=2*(1+0)*1.08МПа*200мм*350мм²=52,92 кНм

с=√ Mb/qsw=√ Mb*s/Rsw*Asw=

=√52,92кНм*150мм/225МПа*

*0,789см²=66,9 см.

Рис. 13

Так как с = 669 мм < 2×h₀ = 700 мм, то это означает, что с = с₀.

Теперь проверяем прочность наклонного сечения

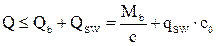
qsw=Asw*Rsw/s=225МПа*0.789 см²/150мм=118,35 кН/м

52,92кНм/669мм+118,35 кН/м*669мм=158,28≥ 124.81 кН

Условие прочности выполняется.

Сечение справа от первой промежуточной опоры:

Расчет на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами производится согласно п. 3.30 [5].

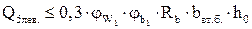
Коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле:

Рис. 12

α=Es/Eb

Рис. 14

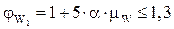
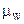Для определения коэффициента необходимо предварительно задаться шагом хомутов в зависимости от высоты сечения второстепенной балки: если она более 450 мм, то шаг хомутов принимается равным 1/3 от высоты второстепенной балки, но не более 500 мм.

Принимаем шаг хомутов 150 мм, а их диаметр из условия свариваемости равным ≥1/3 диаметра продольных стержней, т.е. 10 мм.

Тогда μw=Asw/b*s=0.789/20*15=0.00263

φw1≈1

Коэффициент 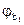определится по формуле:

,

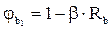где 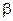=0,01 для тяжелого бетона.

Таким образом, имеем:

0.3*1*0.845*15.3МПа*200мм*350мм=271,49 кН ≥ 104.00 кН

Условие прочности выполняется.

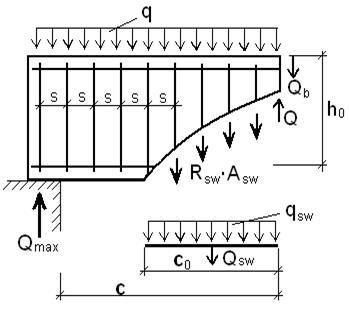Проведем проверку прочности наклонных сечений по поперечной силе. Как показывают опыты, наклонные трещины могут развиваться как непосредственно у опоры, так и на некотором удалении от нее.

В первом случае с=с₀, а во втором – с > с₀.

Определяем значения:

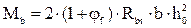
Как говорилось ранее, коэффициент 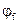=0. Тогда Mb=2*(1+0)*1.08МПа*200мм*350мм²=52,92 кНм

с=√ Mb/qsw=√ Mb*s/Rsw*Asw=√52,92кНм*150мм/225МПа*0,789см²=66,9 см.

Рис. 13

Так как с = 669 мм < 2×h₀ = 700 мм, то это означает, что с = с₀.

Теперь проверяем прочность наклонного сечения

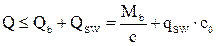
qsw=Asw*Rs/s=225МПа*0.789 см²/150мм=118,35 кН/м

52,92кНм/669мм+118,35 кН/м*669мм=158,28≥ 104.00 кН

Условие прочности выполняется.

3.6. Построения эпюры материалов.

Для построения эпюры материалов используем определенные ранее эпюру огибающих моментов и значения М_u с принятым армированием пролетных и опорных сечений.

Над первой промежуточной опорой

При 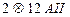с А_S=226мм² (таблица 22 [4]).

μ=Аs/ b*h0=2,26см²/250мм*350мм=0,0026

x = μ*Rs/Rb=0.0026*280 МПа/15.3МПа=0.047

M=z*Rs *Аs*h0=0.975*280 МПа*2,26см²*350мм=21,59 кНм

Мк2=Аs2* Rs*z* h0=0.855*350мм*280 МПа*14,73см²=123.42кНм

В крайнем пролете

При 2Æ25 (A^k_S = 9,820 см²)

μ=Аs/ b*h0=9,82см²/350мм*1250мм =0,0022

x = μ*Rs/Rb=0.0022*280 МПа/15.3МПа=0.04

M=z*Rs *Аs*h0=0.980*280 МПа*9,82см²*350мм=94.31 кНм

Мк1=Аs1* Rs*z* h0=0.965*350мм*280 МПа*(6,28+9,82)см²=152,26 кНм

В среднем пролете

При 2Æ22 (A^k_S = 7,600 см²)

μ=Аs/ b*h0=7,60см²/350мм*1250мм =0,0017

x = μ*Rs/Rb=0.0017*280 МПа/15.3МПа=0.03

M=z*Rs *Аs*h0=0.985*280 МПа*7,60см²*350мм=73.36 кНм

Мк2=Аs2* Rs*z* h0=0.975*350мм*280 МПа*(7,600+3,080)см²=102.05кНм

Над второй опорой

При 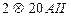с А_S=628мм² (таблица 22 [4]).

μ=Аs/ b*h0=6,28см²/250мм*350мм=0,007

x = μ*Rs/Rb=0.007*280 МПа/15.3МПа=0.13

M=z*Rs *Аs*h0=0.935*280 МПа*6,28см²*350мм=57,54 кНм

Мк2=Аs2* Rs*z* h0=0.875*350мм*280 МПа*14.73см²=126.31кНм

Точка пересечения линий, соответствующих уровню несущей способности, с огибающей эпюрой называются точками теоретического обрыва, фактически стержни обрываются с учетом их заделки в бетоне на величину.

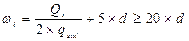
qsw=Asw*Rsw/s=0,789см²*225МПа/150мм=118,35 кН/м

w1л=45.759/2*118.35+5*25=318мм≥20*25=500мм

w1п=54.086/2*118.35+5*25=354мм≥20*25=500мм

w2л=73.431/2*118.35+5*25=435мм≥20*25=500мм

w2п=59.375/2*118.35+5*25=375мм≥20*25=500мм

w3л=33.794/2*118.35+5*22=252мм≥20*22=440мм

w3п=33.794/2*118.35+5*22=252мм≥20*22=440мм

w4л=68.601/2*118.35+5*25=415мм≥20*25=500мм

w4п=70.712/2*118.35+5*25=423мм≥20*25=500мм

Дата добавления: 2015-10-21