Процентные точки и квантили распределения

Существуют определенные числовые характеристики, которые описывают месторасположение одной части выборки относительно остальной части упорядоченной выборки. Рассмотрим понятие процентиля, с помощью которого локализуются позиции наблюдений относительно всей выборки.

Процентили – это числа, обозначаемые через , которые делят исследуемую выборку на 100 равных частей.

1 %

1 %

1 %

…

1 %

1 %

1 %

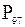
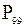
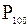
Определение 2.26k-ым процентилем упорядоченной выборки (0 100) называется число 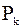, удовлетворяющее двум условиям:

1) в выборке имеется не более k % значений, меньших числа ;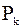

2) в выборке имеется не более % значений больших числа .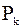

Не более k %

Не более (100 – k) %

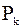
Например, если двадцатый процентиль 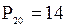, то в выборке содержится не более 20 % значений, меньших 14, и не более (100 – 20) % = 80 % значений, больших 14. Очевидно, что 50-й процентиль 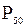совпадает с медианой выборки: 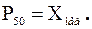Нулевой процентиль 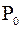является наименьшим выборочным значением. Сотый процентиль 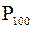равен наибольшему выборочному значению.

Более часто используемыми характеристиками локализации отдельных частей выборки являются так называемые квартили. Квартили – это числа, обозначаемые через которые делят упорядоченную выборку на четыре части:

25 %

25 %

25 %

25 %

Первый квартиль выборки 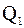совпадает с 25-м процентилем выборки, то есть 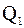является числом, большим не более 25 % выборочных значений, и меньшим не более 75 % значений.

Второй квартиль является медианой. Третий квартиль совпадает с 75-ым процентилем. Число делит выборку на две части: первая часть, содержащая значения меньшие числа , составляет не более 75 % выборки, вторая часть, содержащая выборочные значения, большие числа , составляет не более 25 % выборки. Итак, , , .

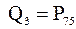Дата добавления: 2015-10-21