Геометрическое среднее и гармоническое среднее

Существуют определенные генеральные совокупности, для которых больше подходят другие виды средних. Рассмотрим понятия среднего геометрического и среднего гармонического.

Определение 2.6Средним геометрическим выборки x ₁, x ₂, …, x _n с положительными значениями называется число 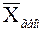, равное корню n-ой степени из произведения всех элементов выборки:

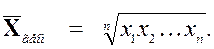
Пример 2.15 Рассмотрим данные о посещаемости студентами группы консультаций по высшей математике. На первой консультации присутствовало 3 студента, на второй – 6, на третьей – 12 студентов.

Итак, выборка состоит из трех значений: 3, 16, 12, n = 3. Вычислим среднее геометрическое по формуле:

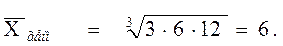
Для сравнения вычислим и среднее арифметическое:

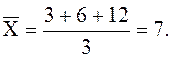
Оба эти значения 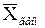= 6 и 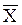= 7, являясь достаточно близкими, характеризуют среднее число студентов, присутствующих на одной консультации. Заметим, что

.

■

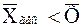В общем случае выборочное среднее и среднее геометрическое связаны неравенством:

.

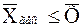Отметим, что формула, определяющая среднее геометрическое, не слишком удобна для расчетов. Поэтому она предпочтительно используется в другом виде:

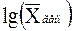
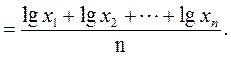
Пример 2.16 Рассмотрим показатели доходности инвестиций финансового фонда в течение пяти последовательных лет:

3,2; 4,5; 7,4; 8,1; 10,5.

Найдем среднее геометрическое этой выборки:

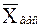
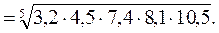
Для вычислений используем логарифмическую формулу:

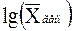
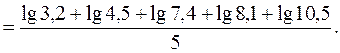
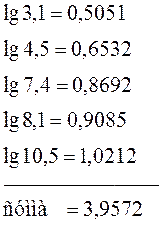
Значит,

.

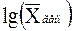
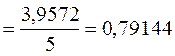Отсюда получаем, что 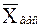= 6,14.

Мы получили среднегодовой показатель доходности инвестиций в течение данного пятилетнего периода.

■

Необходимость использования среднего геометрического возникает при исследованиях темпов изменения величин, когда результаты последующих измерений пропорционально зависят от ранее достигнутых значений. Среднее геометрическое дает более точную характеристику центра выборки и в том случае, когда она состоит из ряда достаточно отдаленных друг от друга значений.

Решим следующую простую задачу.

Автомобиль половину пути проехал со скоростью 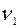км/час, а вторую половину – со скоростью 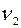км/час. Какой была средняя скорость автомобиля на этом пути?

Обозначим через 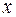расстояние, равное половине пути. Тогда время, затраченное на первую половину пути равно 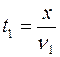, а на вторую – 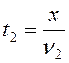. Время всего движения составляет 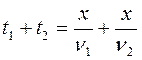. Значит, средняя скорость на всем пути равна:

.

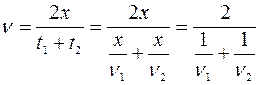Итак, средняя скорость движения определяется выражением:

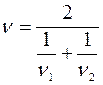
В общем случае для подобных задач существует понятие среднего гармонического.

Определение 2.7Средним гармоническим выборки x ₁, x ₂, …, x _n называется число 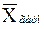, которое вычисляется по формуле:

.

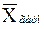
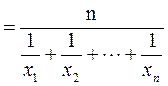Другими словами, среднее гармоническое получается делением объема выборки n на сумму обратных чисел для выборочных значений.

Пример 2.17 За один час работы на компьютере первый студент набрал 2 страницы текста, второй – 3 станицы, третий – 6, четвертый – 12. Найдем среднее гармоническое числа страниц, которые может набрать на компьютере за один час студент этой группы.

Мы имеем выборку из четырех наблюдений:

2, 3, 16, 12.

Вычислим среднее гармоническое:

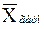
Следовательно, можно предполагать, что в среднем студент этой группы может набрать 3,69 станицы за один час.

■

Определение 2.8 Средним гармоническим вариационного ряда x ₁, x ₂, …, x _n с соответствующими частотами 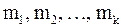называется число 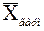, которое вычисляется по формуле:

.

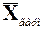
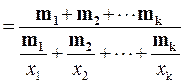Пример 2.18 На решение одной задачи два студента тратят по 10 минут, 3 студента – по 20 минут, 5 студентов – по 30 минут, 4 студента – по 40 минут. Найдем среднее гармоническое времени, необходимого на решение одной задачи.

По данным задачи составим вариационный ряд.

Таблица 2.15 – Затраты времени студентов на решение задачи

Время

Вычислим среднее гармоническое:

.

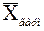
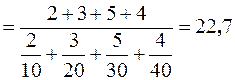Итак среднее гармоническое времени, необходимого для решения одной задачи для этой группы студентов составляет 22,7 минут.

Мы видим, что 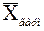= 22,7 меньше 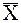= 27,8.

■

Подчеркнем, что во всех случаях среднее гармоническое, среднее геометрическое и среднее арифметическое удовлетворяют неравенству:

.

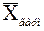
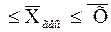Понятие среднего гармонического используется при исследовании некоторых физических, химических, биологических явлений, а также в экономике.

Мы рассмотрели несколько разных понятий выборочных характеристик среднего. Поэтому применение любого из них необходимо сопровождать дополнительным пояснением.

Дата добавления: 2015-10-21