экзаменационных тестовых вопросов для студентов 1 курса,

Фармация» мамандықтарында оқитын бірінші курс студеттеріне математика пәнінен 2-ші семестрдегі емтиханға арналған 360 сұрақтан құрастырылған тест тапсырмалары.

экзаменационных тестовых вопросов для студентов 1 курса,

обучающихся по специальности «Фармация»

1. Екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеу:

Линейное однородное дифференциальное уравнение II порядка с постоянными коэффициентами:

a) y`+py`+qy=0

b) F(x,y,y`,y``)=0

c) f₁(x)j₁(y)dx+ f₂(x) j₂(y)dy=0

d) F(x,f(x),f`(x),f``(x),…,fⁿ(x))=0

e) y``+py`+qy=0

2. Екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеудің шешімі:

Решение линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами:

a) y=e^kx

b) y=Cx

c) y=C+e^kx

d) y=x+C

e) y=ke^x

3. Екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеулер шешу әдісі:

Метод решения линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами:

a) Клеро

b) Коши

c) Эйлер (а)

d) Лагранж (а)

e) Бернулли

4. Егер екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеудің сипаттауыш теңдеуінің дискриминанты 0-ден үлкен болса, онда оның жалпы шешімі:

Если дискриминант характеристического уравнения линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами больше нуля, то его общее решение:

a) y=

b) y=(C₁cosbx+C₂sinbx)e^ax

c) y=e^kx(C₁+C₂x)

d) y=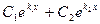

e) y=

5. Егер екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеудің сипаттауыш теңдеуінің дискриминанты 0-ге тең болса, онда оның жалпы шешімі:

Если дискриминант характеристического уравнения линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами равен нулю, то его общее решение:

a) y=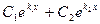

b) y=e^kx(C₁х+C₂)

c) y=

d) y=

e)) y=(C₁cosbx+C₂sinbx)e^ax

6. Екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеуді шешу үшін, оның... теңдеуін құру керек.

Для решения линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами составляется … уравнение.

a) логарифмдік

b) сипаттаушы

c) алгебралық

d) тригонометриялық

e) дәрежелік

a) логарифмическое

b) характеристическое

c) алгебраическое

d) тригонометрическое

e) степенное

7. Екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеуді жалпы шешімі оның сипаттауыш теңдеудің.... таңбасына тәуелді.

Общее решение однородного линейного дифференциального уравнения II порядка с постоянными коэффициентами зависит от знака … соответствующего характеристического уравнения.

a) дискриминанттың

b) белгісіз айнымалының

c) бірінші ретті туындының

d) дифференциалдың

e) екінші ретті туындының

a) дискриминанта

b) неизвестной переменной

c) производной первого порядка

d) дифференциала

e) производной второго порядка

8. Егер екінші ретті коэффициенттері тұрақты біртектес сызықтық дифференциалдық теңдеудің сипаттауыш теңдеуінің дискриминанты 0-ден кіші болса, онда оның жалпы шешімі:

Если дискриминант характеристического уравнения линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами меньше нуля, то его общее решение:

a) y=e^kx(C₁x+C₂x)

b) y=e^x(C₁x+C₂)

c) y=e^kx(C₁+C₂x)

d) y=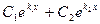

e) y=(C₁cosbx+C₂sinbx)e^ax

9.... дифференциалдық теңдеуге сәйкес келетін k²+2k+5=0 сипаттаушы теңдеу.

Характеристическое уравнение k²+2k+5=0 соответствует... дифференциальному уравнению.

a) y``-2y`+5y=0

b) y``+2y`=0

c) y``+2y`-5y=0

d) y``+2y`+5y=0

e) y``-2y`-5y=0

10. y``-4y`+6y=0 дифференциалдық теңдеуне сәйкес келетін сипаттаушы теңдеу:

Дифференциальному уравнению y``-4y`+6y=0 соответствует характеристическое уравнение:

a) k²+4k-6=0

b) k²+4k=0

c) k²-4k+6=0

d) k²-4k-6=0

e) k²+4k+6=0

11. Толық дифференциалы du= 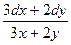болатын функция:

du= 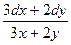является полным дифференциалом от функции:

a) u=ln(3+2y)

b) u=ln(3x+2y)

c) u=

d) u=

e) u=ln(3x-2y)

12. Толық туындылары du=e^3x-2y(3dx-2dy) болатын функция:

du=e^3x-2y(3dx-2dy) является полным дифференциалом от функции:

a) u=e^3x-2y

b) u=3e^3x-2y

c) u=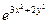

d) u=

e) u=e^3x+2y

13. y``+2y`+5y=0 дифференциалдық теңдеудің шешімі:

Решение дифференциального уравнения y``+2y`+5y=0:

a) y=(C₁+C₂x)e^2x

b) y=(C₁cos2x+C₂sin2x)e^-x

c) y=(C₁cos3x+C₂sin2x)e^-2x

d) y=(C₁e^-x+C₂e^2x)

e) y=(C₁+C₂x)e^-x

14. y``+9y`=0 дифференциалдық теңдеудің шешімі:

Решение дифференциального уравнения:

a) y=C₁e^x+C₂e^-9x

b) y=C₁e^2x+C₂e^-7x

c) y=C₁+C₂e^-9x

d) y=(C₁+C₂x)e^-9x

e) y=(C₁+C₂x)e^x

15. y``-4y`+5y=0 дифференциалдық теңдеудің шешімі:

Решение дифференциального уравнения y``-4y`+5y=0:

a) y=(C₁cosx+C₂sinx)e^-x

b) y=(C₁cos2x+C₂sin2x)e^x

c) y=(C₁cosx+C₂sinx)e^x

d) y=(C₁cosx+C₂sinx)e^2x

e) y=(C₁cosx+C₂sinx)e^-2x

16.... функцияның толық дифференциалы du=(12dx+5dy)e^12x+5y:

du=(12dx+5dy)e^12x+5y - полный дифференциал от функции:

a) u=e^x(12+5y)

b) u=e^12x+5y

c) u=12x+5y

d) u=e^x(12x+5y)

e) u=e^12x+5y

17.... функцияның толық дифференциалы du=lnydx+ :

du=lnydx+ - полный дифференциал от функции:

a) u=xlny b) u=x+lny c) u=lny+ 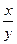d) u=xlny+ 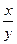e) u=x+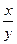

18.... функцияның толық дифференциалы du=e^2x(2sin3ydx+3cos3ydy):

du=e^2x(2sin3ydx+3cos3ydy) - полный дифференциал от функции:

a) u=e^2x-sin3y

b) u=e^2x(sin3y+cos3y)

c) u=e^2x+sin3y

d) u=2e^2xsin3y

e) u=e^2xsin3y

19.... функцияның толық дифференциалы du=(2x+3y)dx+3xdy:

du=(2x+3y)dx+3xdy - полный дифференциал от функции:

a) u=2x+3y b) u=x²+3x c) u=x²+3xy d) u=2x+x³ e) u=x²+x³

20.... функцияның толық дифференциалы du=2[(x-y)dx-(x+y)dy]:

du=2[(x-y)dx-(x+y)dy] - полный дифференциал от функции:

a) u=2x+2y+y²

b) u=2x-2y-y²

c) u=x²-y²-2y

d) u=x²-2xy-y²

e) u=2x-2y-y²

21. теңдеудің жалпы шешімі:

Общее решение дифференциального уравнения :

a) y=(C₁+C₂x)e^-x

b) y=C₁e^4x+C₂e^2x

c) y=(C₁+C₂x)e^4x

d) y=C₁e^-4x+C₂e^-2x

e) y=(C₁+C₂x)e^-2x

22. теңдеудің жалпы шешімі:

Общее решение дифференциального уравнения :

a) y=(C₁cos2x+C₂sin2x)e^x

b) y=(C₁cos4x+C₂sin4x)e^2x

c) y=(C₁cos2x+C₂sin2x)e^4x

d) y=(C₁cosx+C₂sinx)e^2x

e) y=(C₁cosx+C₂sinx)e^-x

23. теңдеудің жалпы шешімі:

Общее решение дифференциального уравнения :

a) y=(C₁x+C₂)e^-3x

b) y=(C₁+C₂x)e^-x

c) y=(C₁+C₂x)e^2x

d) y=(C₁x+C₂)e^4x

e) y=(C₁x+C₂)e^-2x

24. теңдеудің жалпы шешімі:

Общее решение дифференциального уравнения :

a) y=(C₁cos2x+C₂sin2x)e^x

b) y=(C₁cos3x+C₂sin3x)e^2x

c) y=(C₁cos2x+C₂sin2x)e^3x

d) y=(C₁cosx+C₂sinx)e^x

e) y=(C₁cos2x+C₂sin2x)e^-x

25.... функцияның толық дифференциалы du= .

du= - полный дифференциал от функции:

a) u= 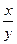. b) u= . c) u=ln 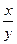. d) u=ln . e) u= .

26.... функцияның толық дифференциалы du= болады.

du= - полный дифференциал от функции:

a) u=ylnx. b) u=xlny. c) u=ln(xy). d) u=lnx+lny. e) u=lnxlny.

27. y=С₁у^2x+С₂у^5x функциясы... теңдеудің жалпы шешімі.

Функция y=C₁e^2x+C₂e^5x - общее решение дифференциального уравнения:

a) y``-10y`+7y=0

b) y``+7y`-10y=0

с) y``+7y`+10y=0

d) y``-7y`-10y=0

e) y``-7y`+10y=0

28. y=у^2x(С₁сosx+С₂sinx) функциясы... теңдеудің жалпы шешімі:

Функция y=e^2x(C₁cosx+C₂sinx) - общее решение дифференциального уравнения:

a) y``+4y`-5y=0

b) y``-4y`-5y=0

c) y``+4y`+5y=0

d) y``-4y`+5y=0

e) y``-5y`+4y=0

29. y=C₁e^x+C₂e^-x функциясы... теңдеудің жалпы шешімі:

Функция y=C₁e^x+C₂e^-x - общее решение дифференциального уравнения:

a) y``-y=0

b) y``+y=0

c) y``+y`=0

d) y``-y`=0

e) y``+y`-y=0

30. y=C₁cos5x+C₂sin5x функциясы... теңдеудің жалпы шешімі:

Функция y=C₁cos5x+C₂sin5x - общее решение дифференциального уравнения:

a) y``-25y=0.

b) y``+25y=0.

c) y``+25y`=0.

d) y``-25y`=0.

e) y``-25y`+25y=0.

31. y=(C₁x+C₂) e^-2x функциясы... теңдеудің жалпы шешімі:

Функция y=(C₁x+C₂) e^-2x - общее решение дифференциального уравнения:

a) y``-4y`-4y=0

b) y``-4y`+4y=0

c) y``+4y`+4y=0

d) y``+4y`-4y=0

e) y``+2y`+4y=0

32. теңдеудің сипаттауыш теңдеуі:

Характеристическое уравнение :

a)

b)

c)

d)

e)

33.... теңдеулері - бірінші ретті сызықтық дифференциалдық теңдеулер болады.

Уравнения... - линейные дифференциальные уравнения первого порядка:

а) 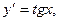б) в) г)

a) б, г

b) а,б

c) а,в

d) б,в

e) в,г

34. 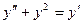дифференциалдық теңдеудің ретін төмендететің алмастыру:

Порядок дифференциального уравнения 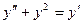понижается путем замены:

a) ,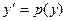

b)

c)

d)

e) ,

35. 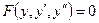дифференциалдық теңдеудің ретін төмендететің алмастыру:

Порядок дифференциального уравнения 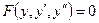понижается подстановкой:

a)

b)

c)

d)

e)

36. y = cos2x функцияның дифференциалы:

Дифференциал функции y = cos²x:

a) cos2xdx

b) –sin2xdx

c) sin²xdx

d) 2cosxdx

e) 2sinxdx

37. y = tgx² функцияның дифференциалы:

Дифференциал функции y = tgx²:

a)

b)

c)

d)

e)

38.... дифференциалдық теңдеудің шешімі y=C₁+C₂e^-5x функциясымен анықталады.

Функцией y=C₁+C₂e^-5x определяется решение дифференциального уравнения:

a) y``-5y=0

b) y``-5y`=0

c) y``+y`=0

d) y``+5y`=0

e) y``+5y=0

39.... дифференциалдық теңдеудің шешімі y=C₁+C₂e^-6x функциясымен анықталады.

Функцией y=C₁+C₂e^-6x определяется решение дифференциального уравнения:

a) y``-6y=0

b) y``-6y`=0

c) y``+6y`=0

d) y``+6y=0

e) y``+y`=0

40.... дифференциалдық теңдеудің шешімі y=C₁cos6x+C₂sin6x функциясымен анықталады.

Функцией y=C₁cos6x+C₂sin6x определяется решение дифференциального уравнения:

a) y``-36y=0

b) y``+36y=0

c) y``-36y`=0

d) y``+36y`=0

e) y``-y`=0

41.... дифференциалдық теңдеудің шешімі y=C₁cos8x+C₂sin8x функциясымен анықталады.

Функцией y=C₁cos8x+C₂sin8x определяется решение дифференциального уравнения:

a) y``+64y=0

b) y``-64y=0

c) y``-64y`=0

d) y``+64y`=0

e) y``-y`=0

42. у=C₁cos10x+C₂sin10x функциясы... дифференциалдық теңдеудің жалпы шешімі.

Функция у=C₁cos10x+C₂sin10x - общее решение дифференциального уравнения:

a) y``-100y=0

b) y``+100y=0

c) y``-100y`=0

d) y``+100y`=0

e) y``-y`=0

43. y=C cosx+C sinx функциясы... дифференциалдық теңдеудің жалпы шешімі.

Функция у= y=C cosx+C sinx - общее решение дифференциального уравнения:

a) y``-y`=0

b) y``-y=0

c) y``+y=0

d) y``+y`=0

e) y``-2y`=0

44. Егер сипаттауыш теңдеудің түбірлері k =1; k =3 болса, онда дифференциалдық теңдеудің жалпы шешімі:

Если корни соответствующего характеристического уравнения k =1; k =3, то общее решение дифференциального уравнения:

a) y=C₁e^-2x+C₂e^2x

b) y=C₁e^-x+C₂e^-3x

c) y=C₁e^-x+C₂e^x

d) y=C₁e^x+C₂e^3x

e) y=C₁e^-x+C₂e^-x

45. Егер сипаттауыш теңдеудің түбірлері k =0; k =5 болса, онда дифференциалдық теңдеудің жалпы шешімі:

Если корни соответствующего характеристического уравнения k =0; k =5, то общее решение дифференциального уравнения:

a) y=C₁e^5x+C₂e^-x

b) y=C₁+C₂e^x

c) y=C₁e^x+C₂e^5x

d) y=C₁+C₂e^3x

e) y=C₁+C₂e^5x

46. Егер сипаттауыш теңдеудің түбірлері k =k =6 болса, онда дифференциалдық теңдеудің жалпы шешімі:

Если корни соответствующего характеристического уравнения k =k =6, то общее решение дифференциального уравнения:

a) y=(C₁x+C₂)e^6x

b) y=(C₁x+C₂)e^x

c) y=(C₁x+C₂)e^-x

d) y=(C₁x+C₂)e^-6x

e) y=(C₁+C₂x)e^6x

47. Егер сипаттауыш теңдеудің түбірлері болса, онда дифференциалдық теңдеудің жалпы шешімі:

Если корни соответствующего характеристического уравнения , то общее решение дифференциального уравнения:

a)

b)

c)

d)

e)

48. Егер сипаттауыш теңдеудің түбірлері болса, онда дифференциалдық теңдеудің жалпы шешімі:

Если корни соответствующего характеристического уравнения , то общее решение дифференциального уравнения:

a)

b)

c)

d)

e)

49. Егер сипаттауыш теңдеудің түбірлері болса, онда дифференциалдық теңдеудің жалпы шешімі:

Если корни соответствующего характеристического уравнения , то общее решение дифференциального уравнения:

a)

b)

c)

d)

e)

50. дифференциалдық теңдеуінің түрі:

Дифференциальное уравнение вида :

a) айнымалыларға байланысты біртекті дифференциалдық теңдеу

b) бірінші ретті біртекті емес сызықты дифференциалдық теңдеу

c) бірінші ретті біртекті сызықты дифференциалдық теңдеу

d) айнымалылары дараланатын теңдеу

e) толық дифференциалдық теңдеу

a) однородное дифференциальное уравнение относительно переменных

b) неоднородное линейное уравнение первого порядка

c) однородное линейное уравнение первого порядка

d) уравнение с разделяющимися переменными

e) уравнение в полных дифференциалах

51. z=f(x,y) функциясының «y»- аргументінен алынған бірінші ретті дербес туынды:

Частная производная первого порядка для функции z=f(x,y) по аргументу «y»:

a) z`<sub>y</sub>, f`_y(x,y), z/ y, f/ y

b) z`<sub>x</sub>, f`_y(y), df/ y

c) z`<sub>x</sub>, f`_y(y), z/ y, f/ y

d) z`<sub>x</sub>, f`_x(x,y), f/ y, f/ x

e) z`<sub>x</sub>, f`_y(y), dz/ y, df/ y

52. z=f(x,y) функциясының «х»- аргументінен алынған бірінші ретті дербес туынды:

Частная производная первого порядка для функции z=f(x,y) по аргументу «х»:

a) z`<sub>x</sub>, f`_x(x,y), dz/dx, df/dx

b) z`<sub>x</sub>, f`_x(x,y), z/ x, f/ x

c) z`<sub>x</sub>, f`(x)_x, z/ x, df/ x

d) z`<sub>x</sub>, f`(y)_x, dz/ x, f/ y

e) z`<sub>x</sub>, f`(x)_x, f/ x, f/ y

53. 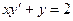дифференциалдық теңдеуінің түрі:

Дифференциальное уравнение вида :

a) бірінші ретті біртекті сызықты дифференциалдық теңдеу

b) айнымалылары дараланатын теңдеу

c) бірінші ретті біртекті емес сызықты дифференциалдық теңдеу

d) айнымалыларға байланысты біртекті дифференциалдық теңдеу

e) толық дифференциалдық теңдеу

a) однородное линейное уравнение первого порядка

b) уравнение с разделяющими переменными

c) неоднородное линейное уравнение первого порядка

d) однородное дифференциальное уравнение относительно переменных

e) уравнение в полных дифференциалах

54. z=f(x,y) функциясының «х»- аргументінен алынған (x,y) нүктесіндегі дербес туындысы деп... шекті айтады.

Частной производной функции z=f(x,y) по аргументу «х» в рассматриваемой точке (x,y) называется предел:

a)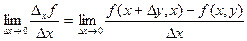

b)

c)

d)

e)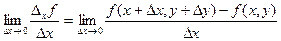

55. – функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции :

a) -5arctgx+C

b) arcсtgx+C

c) -5arcctgx+C

d) 5arctgx+C

e) 0,2arcctgx+C

56. – функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции :

a) +C b) - +C c) +C d) - +C e) 6x⁵+C

57. 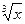– функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции :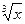

a)

b)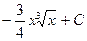

c)

d)

e)

58. y=–5cos5x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=–5cos5x:

a) –5cos5x+C

b)–sin5x+C

c) –5sin5x+C

d) +C

e) +C

59. y=0,8sin8x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=0,8sin8x:

a) 0,8cos8x+C

b) 0,8cosx+C

c)–0,1cos8x+C

d) 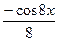+C

e) – +C

60. y=–7sin7x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=-7sin7x:

a) –cos7x+C

b) 7cos7x+C

c) –7cos7x+C

d) cos7x+C

e) +C

61. y=2 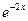функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=2 :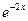

a)–e^-2x +C b) e^-2x+C c) –e^-x+C d) –2e^-2x+C e) e^-x +C

62. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) –0,2e^-2x+C

b) e^-x+C

c) 0,1e^-2x+C

d) 0,2e^-2x+C

e)–0,1e^-2x+C

63. y= 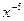функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :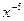

a)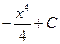

b)

c)

d)

e)

64. y= 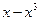функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :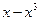

a)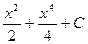

b)

c)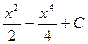

d)

e)

65. y=0,2sin4x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=0,2sin4x:

a) +0,05cos4x+C

b) 0,2cos4x+C

c) –0,2cos4x+C

d)–0,05cos4x+C

e) 0,05cos4x+C

66. y=–0,2sin0,2 функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=–0,2sin0,2x:

a) –2cos0,2x+C

b) –0,2cos0,2x+C

c) 0,2cos0,2x+C

d) +C

e) cos0,2x+C

67. y=3sin2x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=3sin2x:

a) –1,5cos2x+C

b) –3cos2x+C

c) 1,5cos2x+C

d) 3cos2x+C

e) 2cos2x+C

68. y=2 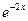функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=2 :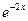

a) e^-x +C

b) –2e^-2x+C

c) e^-2x+C

d) –e^-x+C

e)–e^-2x +C

69. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) arctg2x+C

b) 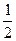arctg +C

c) –2arctgx+C

d) –arctg2x+C

e) 2arctgx+C

70. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) 3arctgx+C

b) –arctg3x+C

c) arctg +C

d) – arctg +C

e) arctg +C

71. y= 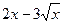функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :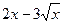

a)

b)

c)

d)

e)

72. y= 8sin4x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=8sin4x:

a) 4cos4x+C

b) –8cos4x+C

c) 2cos4x+C

d) 8cos4x+C

e)–2cos4x+C

73. y=8cos4x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=8cos4x:

a) –8sin4x+C

b) 2sin4x+C

c) 8sin4x+C

d) –2sin4x+C

e) 4sin4x+C

74. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :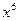

a) +C

b) - +C

c) +C

d) - +C

e) 6x⁵+C

75. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) 2e^x +C b) 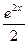c) e^2x +C d) 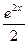+C e) +C.

76. y= 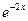функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :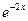

a) e^-x +C

b) e^-2x+C

c) –e^-x+C

d) –2e^-2x+C

e)– 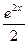+C.

77. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) 2ln|x|+x+C

b) 2ln|x|-x+C

c)

d) x-2ln|x|+C

e) 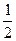ln|x|+x+C

78. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a)

b)

c)

d)

e)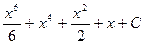

79. функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции :

a)

b)

c)

d)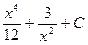

e)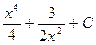

80. y=1 функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=1 :

a) 0,2e^-2x+C

b) 0,6e^-2x+C

c) e^-x+C

d)–0,6e^-2x+C

e) –0,2e^-2x+C

81. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) +C b) 5e^x+C c) e^x+C d) 4e^x +C e) +C

82. y=cos3x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=cos3x:

a) sin3x+C b) sinx+C c) - sin3x+C d) 3sin3x+C e) -3sin3x+C

83. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a)

b)

c)

d)

e)

84. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) –0,8e^-x+C

b) 0,8e^-x+C

c)–e^-0,8x+C

d) –0,8e^-0,8x+C

e) 0,8e^-0,8x+C

85. y= ) функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= ):

a)

b)

c)

d)

e)

86. y= 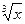функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :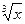

a)

b)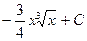

c)

d)

e)

87. y= 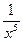функцияның алғашқы функцияларының жиыны:

Для функции 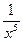совокупностью первообразных является:

a) b) c) d) e)

88. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a)

b)

c)

d)

e)

89. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a)

b)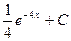

c)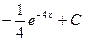

d)

e) 4e^-4x+C

90. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a)

b)

c)

d)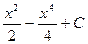

e)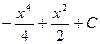

91. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) e^x+C

b) 0,4e^0,4x+C

c) e^4x+C

d) 0,4e^x +C

e) e^0,4x+C

92. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) 0,1e^2x+C b) e^2x+C c) –0,1e^-2x+C d) 2e^2x+C e) e^-2x+C

93. y= 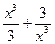функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :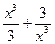

a)

b)

c)

d)

e)

94. у=2cosx функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции у=2cosx:

a) sinx+С

b) sin(x/2)+C

c) 2sinx+C

d) 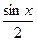+С

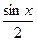e) - +C

95. у=–0,5cosx функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции у=–0,5cosx:

a) – +C

b) 0,5sinx+С

c) +C

d)–0,5sinx+C

e)–0,5sin(x/2)+С

96. у=2cos2x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции у=2cos2x:

a) +C

b) +С

c) 2sin2x+C

d) -2sin2x+С

e) sin2x+C

97. у= 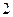функияның алғашқы функцияларының жиыны:

Cовокупность первообразных для функции у= :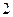

a) 2e^x+C b) e^x+C c) -2e^x +С d) e) +C

98. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) arctg5x+C

b) 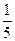arctg +C

c) –arctg5x+C

d) – 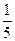arctg +C

e) 5arctgx+C

99. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a)

b)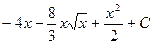

c)

d) .

e)

100. y=0,5 функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=0,5 :

a) b) e^x+C c) e^x-C d) 0,5e^x+C e) +C

101. у= функияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции у= :

a) +C b) 2e^x +C c) 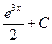d) +C e) e^2x +C

102. y=5sin2x функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=5sin2x:

a) –2,5cos2x+C

b) 2cos2x+C

c) 2,5cos2x+C

d) 5cos2x+C

e) –2cos2x+C

103. y=–6sin2х функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y=–6sin2х:

a) 6cos2x+C

b) 2cos2x+C

c) -3cos2x+C

d) 3cos2x+C

e) –6cos2x+C

104. y= функцияның алғашқы функцияларының жиыны:

Совокупность первообразных для функции y= :

a) e^-x+C

b)–0,1e^-2x+C

c) 0,1e^-2x+C

d) 0,2e^-2x+C

e) –0,2e^-2x+C

Дата добавления: 2015-10-16