Основы физики низкотемпературной плазмы

В плане практических приложений теория плазмы должна обеспечить возмож­ность расчетного определения параметров и свойств конкретного плазменного образования в зависимости от условий ее возникновения и существова­ния. Теория строится на основе пред­ставлений о процессах, протекающих в плазме, что позволяет создать исходную модель и ее математическое отображение. Область применения теории ограничивается областью, в которой справедлива исходная модель.

Заряженные и нейтральные частицы, образующие плазму, обладают определенной кинети­ческой энергией (тепловое движение), а между заряженными частицами действуют мощные кулоновские силы притяжения и отталкивания. Рассмотрение процессов, протекающих в ог­ромной массе взаимодействующих частиц, возможно только статистическими методами. Если такой подход удается осуществить, то из исходного хаоса получают макропараметры среды, функционально зависящие от ее состояния: это температура, давление, теплопроводность, теп­лоемкость, электро­проводность, вязкость.

Вполне удовлетворительная статистическая теория разработана для случая неионизованного газа, она известна под названием кинетической теории газов и опира­ется на модель парных со­ударений частиц. Исходная посылка кинетической теории: силы взаимодействия между микро­частицами любого сорта являются короткодейст­вующими. Поэтому вне тесного сближения двух частиц они движутся свободно, не испытывая взаимных влияний. Такое движение харак­теризуется следующими величинами:

ð импульсом , где – скорость, а – масса частицы;

ð кинетической энергией;

ð внутренней энергией e, определяющей состояние частицы.

При тесном сближении двух частиц они начинают взаимодействовать. Каждая частица рас­сматривается как центр, создающий силовое поле, потенциал которого U(r) зависит от рас­стояния. Очень быстрое (экспоненциальное) уменьшение потенциала с расстоянием объясняет его короткодействие. Продолжительность взаимодействия двух частиц много меньше времени их свободного движения, такой тип взаимодейст­вия называют столкновением частиц. А так как вероятность тройных соударений много меньше вероятности парных, то модель рассматривает все столкновения как парные.

При парном столкновении соблюдаются законы сохранения импульса и энергии. Допустим, частица a сталкивается с частицей b. Общий импульс сталкивающихся частиц:

(2.5)

Обозначим через импульс системы до столкновения, а через – после столкно­вения. Тогда как бы не изменялись импульсы каждой из частиц в результате столкно­вения, общий им­пульс системы не изменится:

Закон сохранения энергии запишем так:

D (2.6)

где De - суммарное изменение внутренней энергии частиц в результате столкновения, 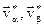– скорости частиц после столкновения.

В зависимости от характера изменения внутренней энергии различают три варианта соуда­рений частиц:

1-ый случай. Внутренняя энергия сталкивающихся частиц не изменяется, De = 0. Такое со­ударение называют упругим.

2-й случай. Часть внутренней энергии системы превратилась в кинетическую энергию дви­жения частиц, De > 0. Пример: столкновение электрона с возбужденным атомом, в результате которого энергия возбуждения перешла к электрону, увеличившему скорость своего движения. Это - неупругое соударение 1-го рода.

3-й случай. Часть кинетической энергии сталкивающихся частиц перешла в потенциальную энергию одной из частиц, De < 0. Пример: электрон при столкновении с атомом передает часть своей кинетической энергии атому и возбуждает или ионизует его. Это – неупругое соударение 2-го рода.

Предсказать движение каждой отдельной частицы в объеме, заполненном множеством таких частиц, невозможно. Однако модель парных соударений позволяет выявить в таком хаотическом движении частиц статистический порядок. Порядок определяется возникновением предсказуемого распределения частиц данного сорта по скоростям и энергиям. Распределение описывается скалярной функцией F(), называе­мой функцией распределения. Здесь вектор определяет положение выделяемого для рассмотрения участка объема, вектор определяет интервал скоростей частиц в данном объеме. Оба вектора в совокупности определяют шес­тимерное фазовое пространство, и функциязадает концентрацию частиц определенного сорта в единице объема этого пространства. Можно сказать и так, что функция распределения Fопределяет зависящую от вре­мени плотность частиц в каждом элементе объема d³r, скорости, которых лежат в данном ин­тервале значений d³v c центром в точке . Несколько позже мы вернемся к рассмотрению особенностей функции распределения и ее роли в статистическом описании макропараметров изучаемой системы, таких как температура, давление, теплопроводность, вязкость и некоторые другие.

Плазма отличается от газа наличием в ней заряженных частиц, которым присущ иной вид взаимодействия – кулоновское взаимодействие зарядов. Это дальнодействующее взаимодействие, при котором одна заряженная частица взаимодействует сразу со многими другими заряженными частицами, и говорить о парных взаимодей­ствиях частиц в этом случае невозможно. Но хотя модель парных столкновений в принципе не применима к газу, находящемуся в состоянии плазмы, в частных случаях возможен компромисс. Например, если концентрация заряженных частиц в газе при большой энергии их теплового движения (высокой температуре) относительно мала, то кулоновские силы проявляют себя умеренно, и их удается свести к эквивалентным парным соударе­ниям между частицами, распространив на такую плазму результаты кинетической теории нейтрального газа. Критерием возможности такого приложения кинетической теории служит понятие идеальной плазмы.

Условие идеальности: число частиц в сфере дебаевского радиуса должно быть большим, >> 1.

Изолированный электрический заряд, плотность которого равна q, создает в свободном пространстве поле, потенциал которого меняется с расстоянием r по закону q/r. Если же заряд помещен в плазму, то возникает эффект его экранировки другими зарядами. В 1923 году Дебаем и Хюккелем было получено математическое решение задачи об экранировке зарядов в объеме. В области, окружающей ион или электрон, потенциал электрического поля меняется с расстоянием по закону:

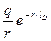(2.8)

Следовательно, влияние заряда на другие заряды уменьшается с расстоянием столь быстро, что это уменьшение можно трактовать как экранировку заряда. Поле сходит на нет на расстоянии

l_D = (2.9)

называемом радиусом экранировки или дебаев­ским радиусом. Соотношение (2.9) с точностью до множителя 2 совпадает с пространственным масштабом квазинейтральной плазмы (2.4). Условие идеальности в уточненном виде запишется так:

>>1 (2.10)

Т – в эВ, n_e – в см^–3. Условие идеальности выпол­няется тем лучше, чем выше температура и чем меньше концентрация электронов в плазме.

Пример: в плазме электроразрядного лазера элек­тронная температура составляет ~2 эВ, а концентрация электронов n_e ~ 10¹⁴ см^{– 3}. Следовательно, ~ 35. Концентрация частиц в дебаевской сфере достаточно велика, чтобы плазму в таком лазере считать идеальной.

В случае идеальной плазмы коллективные кулоновские взаимодействия удается представить как некие эквивалентные парные соударения, благодаря чему кинетические уравнения в несколько измененной форме (в форме уравнения Фоккера – Планка) можно использовать для описания процессов в плазме, получения функции распределения частиц в ней и нахождения интересующих нас ее характеристик.

Дата добавления: 2015-10-16