Столкновения частиц в плазме.

Низкотемпературной плазмой называют среду, температура которой не превы­шает примерно 50000 К. Она представляет собой смесь частиц шести типов: 1) элек­троны; 2) фотоны; 3) атомы (молекулы) в основном состоянии; 4) атомы (молекулы) в возбужденном состоянии; 5) положительно заряженные ионы; 6) отрицательно заряженные ионы.

Совокупность частиц одного типа принято считать одним из «газов» в смеси «газов», образующих плазму. Частицы газа вступают в «реакции» при встрече с частицами другого газа, в результате происходит «разложение» или соединение частиц, их переход из одной группы в другую. Усреднение результатов взаимодействия по большому числу столкновений позволяет определить общее состояние плазмы и характеризующие это состояние макроскопические параметры, если известны кинетические характеристики микрочастиц. Важнейшей такой характеристикой служит функция распределения частиц по скоростям или по энергиям.

Рассмотрим процесс столкновения двух выделенных частиц, например, электрона и атома. Атом рассматривается как силовой центр, создающий короткодействующую силу, способную оказать воздействие на электрон, если он попадет в сферу действия потенциала. Принято считать радиус действия силового потенциала эффективным радиусом самой частицы, в данном случае атома, по отношению к налетающей на нее частицы (электрона). Когда речь идет о среде с большим количеством взаимодействующих в ней частиц, то вводят понятие эффективного сечения столкновения, им характеризуется вероятность свершения индивидуального акта взаимодействия. В случае упругого соударения, когда эффективные радиусы сталкивающихся частиц равны соответственно и , эффективное сечение для них равно:

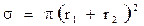
Но если одну из частиц можно считать точечной, то есть , то s = pr².

Обозначим эффективный радиус атома А через r_a. На атом налетает электрон В согласно схеме, изображенной на рис. 2.1. Сфера с центром в точке А – это радиус действия силового потенциала атома или его эф­фективный радиус. Слева от сферы изо­бражена траектория электрона до столкновения. Расстоя­ние этой траектории от оси, проходящей че­рез центр сферы и направленной параллельно трассе электрона, называют прицельным расстоя­нием, обозначим его буквой x (кси). В результате столк­новения изменяется траектория движения элек­трона, и угол d между направлениями тра­ектории до и после столкновения называют углом рассея­ния электрона на силовом центре А. Этот угол представляется как однозначная функция при­цельного расстояния. При лобовом столкновении, когда x = 0, угол d = p и имеет место полное отражение электрона в переднюю полу­сферу, то есть в направлении, обратном его исходному движению. С ростом x угол d®0. Для случая малых углов рассеяния потенциал U(r) много меньше кинетической энергии нале­тающей частицы К, и тогда справедливо соотношение:

d = (2.11)

В зависимости от прицельного расстояния различают близкие и дальние столкновения. Гра­ница между ними – прицельное расстояние, при котором угол d = p/2, то есть тот угол, при ко­тором отражение частиц в переднюю полусферу (близкие столк­новения) сменяется их рассея­нием в заднюю полусферу (дальние столкновения). Наличие большого числа частиц в плазме требует разработки статистического под­хода к рассмотрению процессов их взаимодействия.

В настоящее время отсутствует общая теория коллективных взаимодействий частиц в плазме. Но в частном случае идеальной плазмы удается свести коллективные взаимодействия заряженных частиц к эквивалентным парным соударениям, что позволяет распространить в таких случаях на плазму результаты, полученные в кинетической теории нейтрального газа. Такая возможность связана с существованием эффекта экранировки зарядов. В результате экранировки возникают нейтральные группы разноименно заряженных частиц, а размер каждой такой группы определяется дебаевской длиной экранировки l_D. В случае идеальной плазмы в дебаевской сфере содержится относительно большое число частиц при сравнительно малом радиусе самой сферы. Это позволяет рассматривать подобную сферу как эквивалентную нейтральную частицу, взаимодействующую с другими частицами в форме парных соударений.

По аналогии с кинетической теорией парные столкновения могут происходить либо уп­руго, либо неупруго. Подробности такого рассмотрения плазменных процес­сов представлены в [3,4]. Здесь я ограничусь схематическим изложением основных результатов такого рассмотрения.

Упругие соударения заряженных частиц. При отсутствии экранировки потенциал взаимодействия изолированных заряженных частиц равен:

± (2.12)

где Z₁ – заряд иона, e_о – диэлектрическая проницаемость вакуума. В классическом приближении при таком значении потенциала взаимодействия угол рассеяния d связан с прицельным параметром x (рис. 2.1) соотношением:

tg = (2.13)

Здесь Z_1, Z₂ – заряды каждой из сталкивающихся частиц, v_o – их относительная скорость, m = m₁m₂ / (m₁ + m₂) - приведенная масса. Если одна из частиц – электрон, то m» m_e.

Необходимо учесть неодинаковость вкладов ближних и дальних кулоновских взаимодействий. Ближние взаимодействия сопровождаются рассеянием на углы d ³ p/2, вероятность таких столкновений очень маленькая по сравнению с вероятностью дальних столкновений, при которых d < p/2. Из (2.13) следует, что при d = p/2 граничное значение x_г, разделяющее ближние и дальние взаимодействия, равно:

x_г = 5,56×10^-4/ Т (2.14)

(Т выражена в К).

В идеальной плазме рассеяние частиц на большой угол при одном столкновении внутри сферы дебаевского радиуса значительно менее вероятно, чем результирующее отклонение на большой угол в результате серии столкновений, в каждом из которых рассеяние происходит на малый угол. Для среднеквадратичного отклонения значение угла рассеяния пробной частицы (электрона), проникающей в плазму на глубину L, определяется соотношением:

<(Dd)²> = 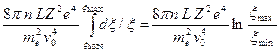(2.15)

потенциал в этом случае можно представить таким:

Если кулоновский потенциал выражается в форме (2.12), то x_max® ¥ и интеграл в (2.15) расходится. Однако учет экранировки позволяет упразднить расходимость, Тогда

x_max = l_D = (kT/ 4p e² n_e)^1/2» 6,9 (T / n_e) (2.16)

Численный коэффициент в правой части справедлив, если температура Т выражена в К. Что же касается параметра x_min, то учет только дальних соударений позволяет считать его равным граничному значению x_г. Обозначим отношение x_max/ x_min = L. Тогда

L» 1,24×10⁴ Т^3/2 (2.17)

(Т – в К, n_e – см ^–3).

Таким образом, если x > x_max = l_D, то потенциал кулоновского взаимодействия заряженной неподвижной частицы в плазме равен нулю и налетающая частица не рассеивается. Если же x_max < x < x_г, при условии, что в сфере дебаевского радиуса n_D >> 1, попадающая в эту сферу подвижная частица будет испытывать множество дальних столкновений и по выходе из сферы она отклонится на некоторый суммарный угол рассеяния d.

В классической теории дифференциальное сечение электрон – ионного взаимодействия определяется формулой Резерфорда:

s_{ei =} (2.18)

Формула остается без изменения и при квантовомеханическом выводе. В прикладных задачах, к которым относится и рассматриваемая нами задача о процессах газоразрядной накачки СО₂ лазера, интегральным следствием парных соударений считается общее число рассеянных налетающих частиц в единицу времени независимо от угла рассеяния. Тогда доля рассеянных в потоке частиц определяют через понятие полного сечения рассеяния, которое называют транспортным сечением. Транспортное сечение, получаемое с учетом потенциала экранировки и различия удельного вклада близких и дальних столкновений, для электрон-ионных столкновений дается соотношением:

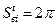
sind dd = 4p lnL» 3,9×10 ^{– 6}×lnL/ T² (2.19)

Логарифм lnL назван кулоновским логарифмом. Соотношение (2.19) справедливо в случае идеальной плазмы. Тогда оно дополняется еще двумя соотношениями, определяющими транспортные сечения электрон–электронных и ион–ионных столкновений:

= 16p(e²/m_ev²)² ln L_e= 1,56×10 ^{– 5} ln L_e/T² (2.19а)

= 16p(e²/m_ev²)² ln L_i = 1,56×10 ^{– 5} ln L_i/T² (2.19b)

Здесь Т – в К, n_e – в см^-3, v – в cм/c.

Знание транспортного сечения позволяет определить следующие характеристики плазмы:

Частота кулоновских столкновений:

= n_e v = 2,6 n_e ln L (2.20)

Среднее время между столкновениями:

= 1/ = 0,38 T^3/2/ n_e ln L (2.21)

Длина свободного пробега:

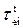= v = 2,5×10⁵ T² / n_e lnL (2.22)

Конкретные расчеты, позволяющие определить из соотношений теории столкновений частиц основные макроскопические характеристики системы, проделываются по одному из двух возможных вариантов.

Первый вариант. Функция распределения частиц по скоростям известна. Тогда транспортные сечения усредняются по функции распределения и вводятся понятия средней скорости и среднего сечения взаимодействия частиц. На их основе рассчитываются переносные коэффициенты – теплопроводность, электропроводность, вязкость, диффузия.

Второй вариант. Функция распределения неизвестна. Ее определение может быть получено решением интегро-дифференциального кинетического уравнения Фоккера-Вульфа, что представляет собой весьма непростую задачу [4].

Неупругие соударения. Наиболее значимые про­цессы, осуществляющиеся при неупругих соударениях: возбуждение, ионизация атомов (молекул) и обратные им процессы ударной дезактивации и рекомбинации. Коротко остановимся на этих процессах.

Возбуждение атомов электронными ударами. Неупругое столкновение свободного электрона с ато­мом может привести к передаче части кинетической энергии электрона атому с переводом его из основного в возбужденное состояние. Для воз­буждения атома как минимум нужна энергия DЕ_min = E_n - E_o, где Е_n, E_o соответственноэнергии верхнего и основного уровней перехода. Обычно эта величина составляет несколько эВ. Участвующий в столкновении свободный элек­трон должен обладать кинетической энергией, превышающей этот порог возбуждения. Но об­ладания кинетической энергией, превышающей порог возбуждения, еще недостаточно для реали­зации такого процесса. Существует вероят­ность того, что при столкновении произой­дет именно акт возбуждения атома, а не рассея­ние нале­тевшего электрона. Эту вероятность называют сечением возбуждения. Расчет сече­ния возбуж­дения сложен и чаще его величину определяют экспериментально. Она является функцией энергии налетающего электрона К_е. Например, в частном случае (для атомов ксенона и аргона) функции возбуждения представлены на рис. 2.2. Для других атомов общая конфигурация зависи­мостей будет такой же. Характерная особен­ность этих функций – нали­чие максимума при вполне определенном для данного атома значе­нии кинетической энергии налетаю­щего элек­трона.

Ионизация атомов электронными ударами. Ионизация – предельный случай возбужде­ния, когда энергия, передаваемая электроном атому, превышает предельное значение DЕ = Е_i – E_o, при котором атомное ядро еще способно удерживать около себя электрон в связан­ном состоянии. Ионизация не требует точной дозировки пере­даваемой атому энергии, так как любое превышение энергии ионизации передается освободившемуся электрону в форме кинетической энергии его дальнейшего движения.

Детальное рассмотрение процесса ионизации позволяет выделить в нем дополнительные черты. Так, первичный электрон, вызвавший ионизацию, смещает атомные электроны отно­сительно ядра. В результате у атома появляется индуцируемый электрический дипольный момент (поляризация). Степень поляризации тем выше, чем выше атомный номер, она также сильно зависит от скорости (энергии) первичного электрона. Подобные эффекты усложняют проведение расчета энергии и вероятности ионизации атома, обе эти величины предпочи­тают определять экспериментально. В таблице 2.1 приводятся первые ионизационные потенциалы некоторых атомов и молекул, которые могут нам понадобиться впоследствии.

Таблица 2.1

Атом (молекула)	H	He	N	O	Ne	Ar	Cu	N2	O2	CO2	H2O
Ui, B	13,5	24,5	14,5	13,5	21,5	15,7	7,7	15,5	12,2	13,7	12,6

Радиационное возбуждение и ионизация. Процессы возбуждения и ионизации атомов (молекул, ионов) могут протекать и в результате поглощения ими квантов электромагнитной энергии с требуемыми свойствами, как это описано в параграфе 1.1. К сказанному ранее следует добавить, что в случае, когда переданная фотоном энергия превышает энергию ионизации, то получивший ее электрон покидает атом и переходит в свободное состояние. Параметр, определяющий вероятность процесса, называют сечением фотовозбуждения или сечением фотоионизации.

Дата добавления: 2015-10-16