Электроразрядная накачка СО2 лазера

Теперь мы можем перейти к центральному вопросу – существует ли разряд, в котором выполняются сформулированные выше требования: при практически холодном газе электронная температура должна быть порядка двух электрон-вольт. Такой разряд существует, он называется тлеющим разрядом, и если бы его не было, то не существовал бы и СО₂ лазер.

Тлеющий разряд. В технических устройствах и в научных исследованиях используются разряды различных типов, отличающиеся давлением газа, силой разрядного тока, условиями отвода тепла и другими характеристиками. Для создания в разряде инверсной населенности (для лазерной накачки) необходим разряд особого типа. В случае смеси двух газов – СО₂ и N₂ – пригодным для этих целей стал тлеющий разряд, самоподдерживающийся разряд с холодным катодом. Характерный признак тлеющего разряда – наличие в нем области катодного падения напряжения, в которой образуется большой по величине объемный положитель-ный заряд.

Протяженность этой области порядка нескольких сантиметров, и на этом участке падение напряжения достигает значений от примерно 100 до 400 В и больше. Если расстояние между катодом и анодом меньше того, которое необходимо для образования катодной области, то разряд не возникает. При расстояниях между электродами от 10 см и выше за областью катодного падения образуется положительный столб, отделяемый от анода относительно узкой областью

анодного падения напряжения.

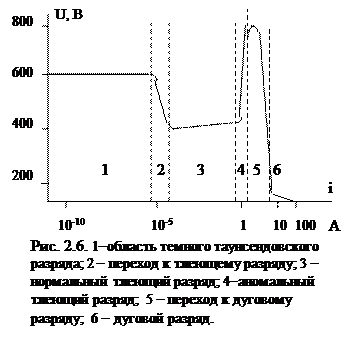Для накачки СО₂ лазеров используется положительный столб тлею­щего разряда. Он представляет собой слабо ионизованную плазму, поддерживаемую внешним электрическим полем. Тлеющий разряд может существовать при давлениях газа от 10^{- 2} до 10 тор и разрядных токах, не превышающих ~10^-1 А. При очень низких токах или давле­ниях вместо него образуется так называемый темный таунсендов­ский разряд. Превышение током или давлением указанных верхних пределов, как видно из графика на рис. 2.6, переводит тлеющий разряд в дуговой разряд, протекающий уже не при холодном, а при горячем катоде. Дуговой разряд неприемлем для накачки СО₂ лазеров.

Тлеющий разряд изучается уже более 100 лет, его подробности описаны во всех учебниках и монографиях, посвященных электрическим разрядам в газах. Кроме областей катодного и анодного падений напряжения и положительного столба в разряде этого типа выделяют и другие структурные детали, которые для наших целей не представляют интереса. Для ознакомления с тлеющим разрядом во всех деталях можно рекомендовать, например [3].

Тлеющий разряд создается в разрядной трубке, представляющей собой обычно цилиндрическую стеклянную трубку радиуса R, в торцах которой по ее оси устанавливаются противостоящие электроды – анод и катод. Нижний предел радиуса трубки определяется условием: l_e << R, где l_e - длина свободного пробега электрона. Под действием внешнего электрического поля напряженностью Е, поддерживающего горение разряда, в плазму положительного столба передается энергия. Непосредственными приемниками энергии поля являются заряженные частицы, прежде всего электроны, как наиболее легкие из этих частиц. Поскольку классический тлеющий разряд может существовать лишь при низких давлениях газа (не более 10 тор) и при слабых токах, то вероятность столкновения электронов с молекулами газа в столбе разряда невелика, и объемными процессами ионизации и рекомбинации в первом приближении можно пренебречь. Источником электронов служит область катодного падения напряжения, выполняющая по отношению к столбу роль своеобразного катода. Однако пусть не очень частые неупругие столкновения электронов с молекулами азота не сопровождаются ионизацией, но они возбуждают эти молекулы, а энергия их возбуждения передается при межмолекулярных столкновениях молекулам углекислого газа, обеспечивая направленное заселение верхнего лазерного уровня.

В области столба разряд заполняет все сечение трубки, если её радиус ограничивается условием: l_e << R, где l_e – длина свободного пробега электрона. Обычно речь идет о радиусе порядка 1,5 см. Сразу после включения разряда протекает процесс диффузии электронов на стенки трубки, в результате на них возникает отрицательный заряд, создающий поперечное электрическое поле. Это поле тормозит, а затем и полностью прекращает диффузию одиночных электронов на стенки. Но возникает новый тип диффузии, получивший название амбиполярной диффузии. Электроны объединяются, но не рекомбинируют, с ионами и в таком парном нейтральном единстве движутся к стенкам, где рекомбинируют и отдают стенкам тепло. Это тепло через стенки должно выноситься в окружающую среду.

Особенности классического тлеющего разряда таковы, что не могут обеспечить получения больших мощностей в лазерном луче. В дальнейшем будет показано, что проблему увеличения мощности СО₂ лазера удалось решить благодаря открытию разновидности тлеющего разряда, при которой основные его особенности – диффузная форма разряда, отрыв электронной температуры от температуры молекул газовой среды, удалось сохранить при высоких давлениях и больших токах. При такой форме разряда объемные процессы ионизации и рекомбинации протекают в объеме положительного столба, а вынос тепла осуществляется потоком газа через зону разряда, не вовлекая в эти процессы стенки разрядной камеры. В этой связи имеет смысл рассмотреть основные особенности газоразрядных процессов, возникающие не только при классической форме тлеющего разряда.

Прикладываемое к электродам разрядного промежутка напряжение вызывает протекание электронного тока от катода к аноду и ионного тока в обратном направлении. Направленное движение зарядов накладывается на хаотическое (тепловое) движе­ние всех газовых частиц. Основную энергию от продольного электрического поля получают электроны, но дальнейшее их движение сопряжено с взаимодействиями с тяжелыми частицами газовой среды, протекающими как упруго, так и неупруго, что сопровождается изменениями движения и обменом энергией с этими частицами. В таких условиях направленная составляющая движения зарядов (ток) проявляется как относительно слабый дрейф зарядов и этот эффект называют переносом зарядов, а характеризующий направленность коэффициент называют коэффициентом пере­носа. Оценка отношения скорости переноса к скорости теплового движения v:

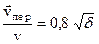, где d = 2m/ M» 10^{– 4}¸ 10^{– 5} (2.39)

Таким образом, скорость переноса на 2 порядка меньше скорости теплового движения частиц. В случае переноса элек­трических зарядов плот­ность тока 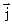и скорость переноса пропорцио­нальны напряженности электрического поля :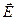

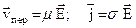(2.40)

Коэффициент пропорцио­нальности m называют под­вижностью, а коэффици­ент пропорциональности s – удельной электропро­водностью. Оба коэффи­циента связываются с мик­рохарактеристиками среды. Так, уравнение движения электронов

(2.41)

где заряд электрона е = 4,8×10^–10 СГСЭ = 1,6×10^–19 Кл в СИ, масса электрона m_e= 9,1×10^{– 28} г, n_m – частота столкновения электрона с другими частицами. В слу­чае стационар­ности (уста­новившееся горение разряда) dv_eпер/dt = 0 и

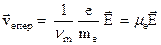(2.40а)

откуда находится подвижность электронов:

m_е = 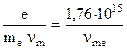(2.42)

Если размерность n- в [c^{- 1}], то размерность m будет [см²/(В×с)]. Соответственно для подвижно­сти ионов получено соотношение:

m_i = 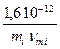(2.42а)

В таблице 2.3 приведены экспериментальные значения подвижности электронов в инте­ресующих нас газах. Подвижность электронов всегда на несколько порядков больше подвижности ионов, то есть m_e >> m_i. В таблице 2.4 даны экспериментальные значения подвижности ионов в собственном газе, которые можно сравнить со значе­ниями m_е из предыдущей таблицы. Поскольку плотность электрического тока в разряде равна:

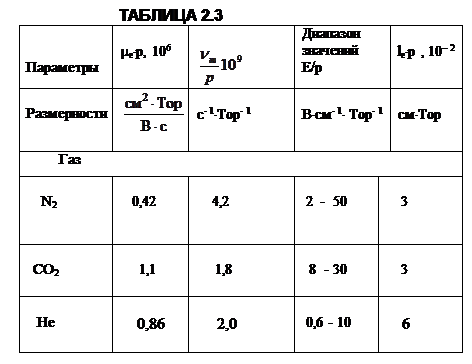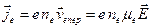(2.43)

то удельная электропроводность:

s = e n_e 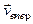= = 2, 82×`10^{- 4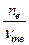} (2.44)

Если n_е – в см^{- 3}, а n_me – в с^{- 1}, то s – в Ом^{- 1}×см^{- 1}. В литературе можно встретить вместо Ом^{- 1} другое название единицы электропроводности – Сименс: См = Ом^{- 1}.

Таким образом, для определения удельной электропроводности плазмы, этой характери­стики переноса электриче­ских зарядов, необходимо знать частоту столкновений соответствующих частиц при их движении во внеш­нем электрическом поле. Эту частоту следует усред­нить по всему ансамблю данных частиц, воспользовавшись функцией их распределения по скоростям. На подробностях такой процедуры здесь нет смысла останавливаться, она рассматрива­ется в курсах физики плазмы, например в [4,5].

Общие представления о процессах, происходящих при электрических разрядах в газах, конкретизируются при рассмотрении положительного столба тлеющего разряда следующим образом. Характеристики столба вдоль оси меняются слабо, что позволяет считать градиент потенциала в этом направлении постоянным, не зависящим от общей длины столба: dU/dx = const. Отсюда следует, во-первых, что средняя энергия электронов также постоянна вдоль оси, то есть электронная температура постоянна T_e(x) = const. Во-вторых, так как d²U/dx² = 0, то в каждой точке вдоль оси соблюдается условие квазинейтральности: n_e = n_i.. В радиальном направлении не сохраняется однородность пространственного распределения параметров. Для оценочных прикидок параметров положительного столба тлеющего разряда можно воспользоваться приведенными соотношениями и экспериментальными данными, содержащимися в таблицах 2.3, 2.4.

Обычно классический тлеющий разряд создается в разрядной трубке, представляющей собой цилиндрическую стеклянную трубку радиуса R, в торцах которой по ее оси устанавливаются противостоящие электроды – анод и катод. Как отмечалось выше, рекомбинация наиболее активно происходит на стенках разрядной трубки, куда электроны и ионы попарно попадают в результате амбиполярной диффузии, поскольку объемная рекомбинация оказывается маловероятной. Что же собой представляет диффузия и, в частности, амбиполярная диффузия?

Диффузией в газе называют процесс перемещения заряженных или нейтральных частиц из области с большей их концентрацией в область с меньшей концентрацией. Скорость диффузии частиц в собственном газе определяется соотношением:

v_д = - D (2.45)

где n - концентрация частиц, а D – коэффициент диффузии. Если v_д выражена в см/с, n – в см^{- 3}, то размерность D – см²/с. При протекании диффузии только в направлении оси Х ее скорость определяется соотношением:

v_д = 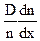(2.46)

Из кинетической теории газов следует, что коэффициент диффузии ионов в собственном газе равен:

D_i = l_i / 3 (2.47)

- средняя тепловая скорость ионов, l_i – длина их свободного пробега. Например, экспериментально определенное значение коэффициента диффузии ионов в азоте при давлении 1 тор равно ~ 23 см²/ с, а в СО₂ – 18 см² / с.

Для электронов коэффициент диффузии выражается в такой же, как и для ионов, форме

D_e = » 2×10⁵×l_e 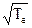(2.48)

Обычные значения D_e для интересующих нас газов порядка 10⁵ см²/с, то есть D_e >> D_i. Так как l_i ~ T/ p, то при Т = const имеем D_i×p = const, а при p = const D_i ~ T^3/2. Среднее перемещение иона за время t: x = .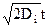

Из теории также вытекает, что коэффициент диффузии связан с подвижностью заряженной частицы соотношением Эйнштейна:

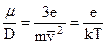(2.49)

Для ионов, температура которых примерно равна температуре нейтральных частиц, правая часть (2.49) приводится к виду:

(2.50)

а для электронов, когда Т_е>Т_i, введение давления p невозможно и для них соотношение сохраняется в виде (2.49) с заменой Т на Т_е.

В столбе тлеющего разряда под действием продольного электрического поля между электродами осуществляется диффузионный процесс переноса зарядов, создающий электрический ток разряда. При этом протекают процессы неупругих столкновений электронов с молекулами, сопровождающиеся возбуждением молекул газа. Одновременно происходит диффузия заряженных частиц и в радиальном направлении, от оси разряда к стенкам. Радиальное поле тормозит движение электронов к стенкам и ускоряет движение ионов в этом направлении. При определенной концентрации избыточных электронов на стенке поле достигает такой величины, что скорости диффузии электронов и ионов уравниваются, частицы с разноименными зарядами начинают двигаться к стенке попарно и там рекомбинировать. Такой тип диффузии впервые изучил и теоретически описал Шоттки в 1924 году. Он же назвал такую диффузию амбиполярной.

Пусть выполняется условие: |n_i – n_e| << n_e. Электроны и ионы движутся с одинаковой скоростью к стенке и эта скорость равна:

v_a = – (2.51)

D_a - коэффициент амбиполярной диффузии. С учетом того, что m_e >> m_i и D_e >> D_i имеем следующее выражение для определения D_a:

D_a» 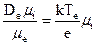(2.52)

(правая часть соотношения получена с учетом формулы Эйнштейна). Напряженность радиального поля Е_R автоматически устанавливается на значении:

E_R» 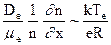(2.53)

где R – характерный масштаб градиента плотно­сти зарядов, в данном случае – это радиус раз­рядной трубки.

Основные следствия теории положитель­ного столба тлеющего разряда. Теория положительного столба классического тлеющего разряда была разработана в своей основе в 20-е – 30-е годы предыдущего века. В положительном столбе заряженные частицы попадают под воздейст­вие как аксиального, так и радиального электриче­ских полей. Здесь коснемся лишь некоторых следствий теории, представляющих интерес для темы данной книги.

а) Радиальное распределение зарядов. Под действием радиального поля протекает амбипо­лярная диффузия заряженных частиц. Уход заряжен­ных частиц из осевой зоны компенсируется их поступлением из зоны катодного объ­емного заряда и отчасти в процессах объемной ионизации, протекающей при неупру­гих соударениях электро­нов с молекулами. Частоту таких соударений обозначим через n_k.

Уравнение баланса заряженных частиц записывается в форме:

(2.54)

Его решением служит бесселева функция нулевого порядка J_o c действительным аргументом

n_r = n_o J_o 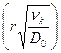(2.55)

где n_о - концентрация заряженных частиц на оси разряда. У стенки (r = R) заряд очень мал, поэтому J_o 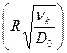» 0, откуда из таблиц бесселевых функций получаем R× 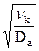= 2,405. Подставив в (2.55) это значение, находим:

n_r = n_o J_o (2,4 r/ R) (2.55а)

Таким образом, распределение зарядов по радиусу трубки близко к параболическому.

б) Связь электронной температуры с на­пряженностью аксиального электрического поля Е_х [3]. Энергия электрона в столбе разряда определяется балан­сом, состоящим из получае­мой им энергии от внешнего электрического поля и поте­рями энергии при столкновениях. Приоб­ретаемая энергия: еЕ_х v_пер. Теряемая энер­гия:

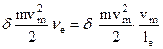
Здесь d = 2m/M – доля теряемой электроном энергии при упругих соударениях. При неупругих соударениях эта доля d >> 2m/M. Так как mv²/2 = kT, то потери можно записать в виде d×kT_ev_m/l_e. Уравнение баланса энергии для электрона выглядит так:

e E_x v_пер = 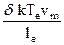(2.56)

Но v_пер/v_m ~ 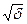и, в конечном счете

T_e[эВ] = 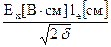(2.57)

в) Электронная температура. Введем обозначение: x = eV_i/kT_e, где V_i – потенциал ионизации. Формула для определения Т_е как функции радиуса трубки R, давле­ния газа р с учетом рода газа находится из соотношения для скорости ионизации в расчете на один электрон:

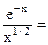1,2×10⁷(С×р×R)²=1 (2.58)

Здесь , a– эффективность ионизации, р – в тор, V_i – в вольтах, m_i – в см²/(В×с), Т_е – в К.

Для интересующих нас газов коэффициент эффективности ионизации «а» приве­дена в таблице 2.5. Расчет облегчается возможностью использования графика, пред­ставленного на рис. 2.7, где приведена зависимость Т_е/V_i от С×p×R [3], (2.70), если учесть оптимальное значение К, начальную

Таблица 2. 5

Газ	Не	N2	CO2	O2
а×10^2	4,6

---

Дата добавления: 2015-10-16