Квазиравновесная и частично равновесная плазма

Термодинамическое равновесие считается одним из возможных состояний макровеще­ства, в том числе и плазмы. Состояние системы, находящейся в термодинами­ческом равно­весии (ТДР), можно описать как функцию двух термодинамических па­раметров, например, температуры и давления. В частности, для описания макроско­пических параметров системы (тепловых, электрических, оптических) нет надобности привлекать к рассмотрению модель микропроцессов, это можно сделать феномено­логическим подходом.

Понятие ТДР внедрилось в науку в XIX веке вместе со сформировавшейся тогда же новой научной дисциплиной – классической термодинамикой. Термодинамика обобщает накоплен­ный человечеством опыт по изучению процессов преобразования одних видов энергии в другие, сопровождаемые совершением работы, прежде всего преобразования тепловой энергии в механическую и наоборот, а также всех остальных видов энергии в тепловую. Но предполагается, что протекание этих процессов происходит в замкнутых системах, которые не обмениваются ни энергией, ни веществом с окружающей средой. К тому же эти системы предполагаются либо равновесными, либо находящимися в состоя­нии, близком к равновесию.

В основе термодинамики лежит небольшое число исходных обобщений опытных данных, сформулированных в форме четырех законов или, следуя исторической традиции, четырех начал термодинамики. Представления о ТДР вытекают из второго начала, определяющего необратимую направленность любых процессов преобразования энергии в замкнутых системах. Уточним содержание терминов, которые используются нами, но о смысле которых иногда забывают.

Энергия. Смысл этого понятия до конца не прояснен, одно из принятых определений таково: это общая количественная мера движения и взаимодействия всех видов материи. Тем не менее, из этого понятия следуют вполне реальные следствия, широко используемые на практике. Например, закон сохранения энергии, представления о существовании различных видов энергии, количественные соотношения при переходах одних видов энергии в другие и т.д. В переводе с греческого энергия означает действие, деятельность. Глубокий смысл этого понятия раскрывается в полученном Эйнштейном соотношении эквивалентности энергии и массы: E = mc², где Е – энергия, m – масса вещества, с – скорость света в вакууме. В термодинамике энергия – это способность системы совершать работу.

Теплота и работа – характеристики способов передачи энергии: система может получить (отдать) энергию либо при нагревании, либо посредством совершения над нею работы. Совершение работы сопровождается сообщением системе частиц упорядоченности движения, а нагревание системы сопровождается нарастающей неупорядоченностью движения ее частиц.

Упорядоченность – взаимно коррелированное расположение частиц (элементов) системы. Упорядоченность проявляется в виде пространственной или временной корреляций.

Структура – определенное расположение, конфигурация частиц или элементов, составляющих систему. Наличие структуры равнозначно наличию упорядоченности.

Замкнутая система – система, не обменивающаяся энергией или веществом или тем и другим с окружающей средой. Иногда замкнутую систему называют изолированной.

Открытая система – система, связанная с окружающей средой и обменивающаяся с ней энергией, или веществом, или тем и другим.

Второе начало имеет несколько эквивалентных формулировок. Например, формулировка одного из основоположников этой дисциплины Кельвина: «Невозможен про­цесс, единственный результат которого состоял бы в поглощении теплоты от нагре­вателя и полного преобразования этой теплоты в работу». Формулировка другого основоположника Клаузиуса: «Невозможен процесс, единственный результат кото­рого состоял бы в переходе энергии от более холодного к более горячему телу». Из обоих определений следует, и это самое главное, что в замкнутой системе при проте­кании любых преобразований энергии будет нарастать количество тепловой энергии, которую невозможно без дополнительных затрат энергии более высокого порядка перевести в другие формы энергии. А так как в замкнутую систему дополнительной энергии не поступает, то внутренние резервы рано или поздно истощаются и тогда господствуют процессы распада существующих упорядоченностей, переход всех высших форм энергии в самую низшую – в тепловую энергию, иначе говоря, проте­кают процессы нарастания хаоса. Концом таких процессов и является достижение системой самого простого и неупорядоченного из всех возможных ее состояний – состояния ТДР.

Количественная направленность процессов преобразования энергии в системе выражается через понятие энтропии S. В замкнутой системе энтропия выражается соотношением, которое одновременно может служить ее определением:

dS = dE/T (2.23)

где dE – сообщенная системе (или отнятая от нее) теплота, Т – температура системы. Таким образом, энтропия – это происходящее в протекающих процессах изменение тепловой энергии системы, отнесенное на один градус температуры. В ходе любых преобразований энтропия замкнутой системы растет. Следовательно, ее можно трактовать как меру неупорядоченности системы. Максимальная неупорядоченность – это состояние ТДР, ему соответствует максимальное значение энтропии: S = S_max. Утверждение, что любые преобразования энергии в замкнутой системе ведут к росту энтропии, достигающей максимального для данной системы значения в состоянии ТДР, служит еще одной эквивалентной формулировкой второго начала.

Каждому термодинамическому состоянию можно приписать вероятность W, связанную с числом возможных способов, которыми это состояние достигается. Чем больше число таких способов, тем выше вероятность того, что данное состояние может реализоваться. Максимально возможной оказывается вероятность состояния, в котором все атомы (молекулы) распределены однородно, а энергия полностью рассеяна. Это и есть уже знакомое нам состояние ТДР. Больцман показал, что в замкнутой системе энтропия есть величина, пропорциональная логарифму вероятно­сти данного состояния:

S = k logW (2.24)

Это соотношение имеет настолько глубокий смысл, что оно было выбито на надгробной плите могилы Больцмана. Понятно, что чем выше упорядоченность системы, тем меньше значение энтропии и тем маловероятнее достижение такого состояния. Этот вывод создал немалые трудности при попытках объяснить происхождение Вселенной и возникновение жизни: и то, и другое событие настолько маловероятно, что с этих позиций невозможно понять, как оно вообще могло реализоваться, если время существования Вселенной не является бесконечным. Но современные представления о Мире не распространяют выводы классической термодинамики на вещественную Вселенную, которая является открытой, а не замкнутой системой.

Итак, любая замкнутая система, какой бы исходной степенью упорядоченности она не обладала, с течением времени непременно перейдет в состояние ТДР. Но современное научное мировоззрение опирается на представления об открытости нашего мира, вокруг себя мы наблюдаем только открытые системы разных масштабов. Среди известных объектов не удается найти замкнутую систему в точном значении этого термина. Можно лишь говорить о той или иной степени приближения к равновесному состоянию тех или иных систем. А это значит, что в известном нам мире не существует как такового состояния ТДР, а есть лишь та или иная степень приближения к нему.

Плазма также существует только в состояниях, с той или иной степенью удаленности от ТДР, поскольку плазма образуется только в открытых системах. Тем не менее, в некоторых частных случаях можно с определенной степенью приближения рассматривать локальные области, заполненные плазмой, как находящиеся в квази­равновесном или ему подобном состоянии. Первой степенью приближения плазмы к равновесности считают установление в ней квазиравновесного распределения частиц одного сорта по скоростям (энергиям). Такое распределение было получено Максвеллом, оно названо максвелловским распределением по скоростям. На практике пользуются иным вариантом скалярной функции, называемой распределением частиц одного сорта по скоростям. Так, при фиксированном значении вектора функция распределения F определяет число частиц одного сорта в данном интервале скоростей , находящихся в определенном локальном местоположении. Для этого случая вводят скаляр f (:

F (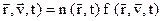 (2.25)

ò f = 1

^(v)

где n ( – концентрация частиц данного сорта в конфигурационном пространстве [5]. Функция f определяет долю частиц, находящихся в данном единичном объеме, скорости которых ле­жат в интервале . Понятно, что интеграл этой функции по всем скоростям частиц в данном объеме равен единице, то есть охватывает все находящиеся там частицы.

Для данного единичного объема максвелловская функция f_v определяется соотношением:

f^M(v) = 4p ×exp ×v² dv (2.26)

Графически в приведенных координатах максвелловская функция распределения частиц по скоростям показана на рис.2.3. Она имеет максимум при скорости v_m – это наиболее вероятная скорость движения частиц данного сорта. Она равна:

v_m= (2kT/m)^1/2 =1,66×10^-8(Т/m)^1/2 (2.28)

От функции распределения частиц по скоростям перейдем к функции их распределения по энергиям:

exp (2.29)

Наиболее вероятная энергия в таком распределении характеризует степень нагретости тела, то есть температуру:

(2.30)

Для частиц сорта a величина Т определяет степень нагретости этих частиц, это температура частиц сорта a и ее можно обозначить символом Т_a. Среди частиц сорта b также может уста­новиться максвелловское распределение, но его наивероятнейшая энергия не обязательно сов­падет с наивероятнейшей энергией частиц сорта a. Таким образом, Т_b ¹ Т_a.

Следующей степенью приближения системы к равновесному состоянию считается случай, когда в многокомпонентной плазме среди частиц каждого сорта устанавливается свое максвелловское распределение, но у частиц каждого сорта оно отличается от распределения среди частиц других сортов. Для конкретности рассмотрим плазму, состоящую из частиц трех сортов: электронов, положительных ионов и атомов (моле­кул). Пусть у частиц каждого сорта установилось свое максвелловское распределе­ние. Степень нагретости частиц каждого сорта характеризуется своей температурой, так что одновременно в плазме сосуществуют три разные температуры: электронная температура Т_е, ионная температура Т_i и атомная температура Т_а. Для плазмы, нахо­дящейся в умеренном внешнем электрическом поле, выполняется условие:

Т_е > T_i > T_a

Состояние такой плазмы называют ионизационным равновесием. В этом случае обнаруживается прямая связь между электронной концентрацией (степенью ионизации) и электронной температурой, которая выражается соотношением, получившим название уравнения Саха:

(2.31)

x_e = n_e/(n_a + n_i); р – давление в тор, Т – в К, U_i – потенциал ионизации в эВ

Из уравнения Саха следует, что электрические и оптические свойства плазмы, нахо­дящейся в состоянии ионизационного равновесия, зависят только от двух термоди­намических параметров – от электронной температуры и давления.

Следующая ступень приближения плазмы к состоянию равновесия – максвелловские функции распределения по энергиям для всех частиц имеют одинаковые значе­ния. Тогда можно написать, что: T_e = T_i = T_a = T. Здесь Т – это единая температура всей системы. Степень ионизации такой плазмы определяется тем же уравнением Саха, но вместо электронной температуры Т_е в нем стоит общая температура Т. Вместо концентрации нейтральных частиц n_a вводится давление газа р, для чего использу­ется известное газокинетическое уравнение:

p = kT×(n_e + n_i + n_а) = kT (2n_e + n_a) (2.32)

Самый правый вариант соотношения справедлив только при условии однократной ионизации плазмы. Эту степень приближения к равновесности называют тепловым равновесием.

В случае ионизационного и теплового равновесия распределение возбужденных атомов по энергетическим уровням при данной температуре Т описывается уравнением Больцмана (1.1):

n_k = n_o×exp (– E_k / kT) (1.1а)

Здесь n_k, n_o – соответственно населенности k-го уровня с энергией E_k, и основного уровня; g_k – кратность вырождения k-го уровня (статвес); G_o- статистическая сумма весов для частиц данного сорта:

(2.33)

Больцмановское квазиравновесное распределение возбужденных частиц по энергетическим уровням показывает, что с ростом энергии уровня его заселенность экс­поненциально падает, так что появление инверсной населенности исключается, следовательно, не могут проявиться лазерные эффекты.

Самым сильным требованием к системе, позволяющим рассматривать ее как максимально приблизившуюся к ТДР, служит условие детального равновесия, когда частоты прямых и обратных процессов строго равны. Так, прямому процессу возбуждения атомов электронным ударом должен количественно соответствовать обратный процесс – девозбуждения атома электронным ударом и так далее. К сказанному остается добавить еще одно квазиравновесное состояние плазмы электрических разрядов в газах – локальное термодинамическое равновесие. О нем подробнее будет идти речь в дальнейшем, при рассмотрении систем оптической накачки лазе­ров. На этом мы завершим краткое знакомство с кинетикой плазменных процессов и рассмотрим особенности молекулы СО₂ как основного элемента активной среды СО₂ лазеров. Для дополнительного более подробного знакомства с физикой плазмы и, в частности, электрического разряда в газах, рекомендуются источники [3-6].

Дата добавления: 2015-10-16