Пример расчета цепи однофазного переменного тока

Расчет выполнен средствами пакета MathCAD.

Для обозначения силы тока, величины напряжения и других электрических величин использованы общепринятые обозначения и единицы измерения. (В, А, Ом, Вт, вар, ВА, Гц, Ф).

При расчетах использованы следующие функции, заданные пользователем:

- вычисление начального угла сдвига фазы синусоиды, заданной комплексом Х (в градусах),

fi(X):=arg(X) ;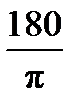

- вычисление угла сдвига фаз между синусоидами, соответствующим комплексам X и Y (в градусах),

ffi (X, Y):= fi(X)- fi(Y).

C1

R1

L3

R3

C2

E

I₁

U_C1

U_R1

U_L3

U_R3

I₃

I₂

U_C2

U_R1C1

U_L3R3

В

А

Рис. 2.3. Исходная схема электрической цепи

R1:= 6 L3:= 95∙10^-3 С1:= 637∙10^-6 С2:= 159∙10^-6

Ом Гн Ф Ф

Е:= 100 R3:= 20 f:= 50

В Ом Гц

1.Находим реактивные сопротивления Х_С1, Х_С2 и Х_L3 элементов исходной схемы:

XC1:=	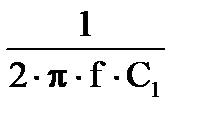XC2:=	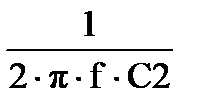XL3:= 2∙p∙f∙L3
XC1 = 4.997 Ом	XC2 = 20.019 Ом	XL3 = 29.845 Ом

2.Составляем расчетную схему цепи и находим комплексные сопротивления ее ветвей:

Z 2

I ₃

U _Z2

U _Z1

Z 1

Z 2

I ₃

E

I 1

Z 3

Z 2

I ₃

I ₂

E

U _Z3

А

В

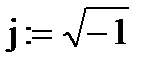
Рис. 2.4. Расчетная схема

Z 1:= R1-j∙XC1 Z 1 = 6.000-4.997j Ом | Z 1| = 7,808 Ом fi(Z 1)= -39.789^0

Z 2:= -j∙XC2 Z 2 = -20.019j Ом | Z 2| = 20,019 Ом fi(Z 2)= -90.000^0

Z 3:= R3+j∙XL1 Z 3 = 20.000 + 29.845j Ом | Z 3| = 35.927 Ом fi(Z 3)= 56.173^0

3. Находим ток и напряжения в ветвях расчетной схемы.

3.1. Комплексное эквивалентное сопротивление расчетной схемы (рис. 2.4) относительно источника ЭДС:

Z:=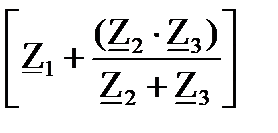

Z:= 22.143 – 32.947j Ом

| Z | = 39.697 Ом

fi(Z)= -56.096^0

3.2. Находим комплексный ток через источник ЭДС:

I 1:=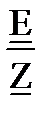

I 1 := 1.405 + 2.091j А

| I 1| = 2.519 А

fi(I 1)= 56.096^0

3.3. Находим комплексные напряжения на сопротивлениях Z₁, Z₂ и Z₃ :

U Z1:= I 1∙ Z 1

U Z1 := 18.879 + 5.523 В

| U Z1 | = 19.670 В

fi(U Z1)= 16.307^0

Сопротивление, эквивалентное параллельно включенным Z₂ и Z_3, равно:

Z _АВ:=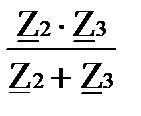

U Z2:= I 1∙ Z АВ U Z3:= U Z2

U Z2:= 81.121 - 5.52 В

| U Z2| = 81.309 В

fi(U Z2)= -3.895^0

Проверка правильности вычислений величин напряжений по второму закону Кирхгофа: U _Z1 + U _Z2 – Е = 0.000 U _Z1 + U _Z3 – Е = 0.000

3.4.Находим комплексные токи ветвей и угол сдвига фаз между током и напряжением ветви:

I ₂:=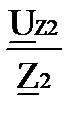

I2:= 0.276 +4.052j А

| I 2|:= 4.061 А

fi(I 2)= 86.105

ffi(I 2, U Z2)= 90^0

I ₃:=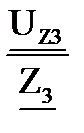

I 3:= 1.129 – 1.961j А

| I 3|:= 2.263 А

fi(I 3)= -60.068^0

ffi(I 3, U Z3)= -56.173^0

Проверка правильности вычисления токов по первому закону Кирхгофа   I ₁ – I ₂ – I ₃ = 0.000   Угол сдвига фаз между током и напряжением ветви должно быть равно углу сдвига фазы комплекса сопротивления ветви   |ffi(I ₁, U _Z1)| = |fi(Z ₁)| |ffi(I ₂, U _Z2)| = |fi(Z ₂)| и т.д.  

3.5. Находим комплексные напряжения на элементах исходной схемы (рис. 2.3):

U С1:= I 1∙(-j∙ X C1)   U С1 = 10.448 - 7.022j B	U R1 := I 1∙R1   U R1 = 8.431 - 12.5j B	U С2 = I 2∙(-j∙ X C2)   U C2 = 8.121 - 5.523j B
| U С1| = 12.588 B   fi(U C1) = -33.904^0   ffi(I 1, U C1)= 90^0	| U R1| = 15.115 B   fi(U R1) = 56.096^0   ffi(U R1, I 1)= 0^0	| U С2| = 1.309 B   fi(U C2) = -3.895^0   ffi(I 2, U C2)= 90^0

U R3 := I 3∙R3   U R3 = 22.585 - 39.22j B   | U R3| = 45.264 B   fi(U R3) = -60.068^0   ffi(I R3, I 3)= 0^0

U L3 := I 3∙j∙ X L3 U L3 = 58.536 + 33.703j B   | U L3| = 67.545 B   fi(U L3) = 29.9^0   ffi(I 3, U L3)= -90^0

Проверка правильности вычисленных напряжений по второму закону Кирхгофа: U _R1 + U _C1 – U _Z1 = 0 U _R1 + U _C1 + U _R3 + U _L3 – E = 0 Разность фаз между током и напряжение должна быть равна 90 ⁰ :   - на конденсаторе ток опережает напряжение на 90⁰ ffi(I ₁, U _C1)= 90⁰   - на катушке индуктивности ток отстает от напряжения на 90⁰ ffi(I ₃, U _L3)=-90⁰ и. т.д.

4. Составляем баланс отдаваемой и потребляемой мощностей.

Комплексная мощность цепи S, отдаваемая источником, определяется как произведение комплекса ЭДС на комплексно-сопряженный ток I ₁^* через этот источник ЭДС:

S:= (E ∙ I ₁^*) S = 140.516 - 209.080j B·A | S | = 251.911 B·A

Мощность, потребляемая элементами цепи S ₁, определяется через затраты мощности на каждом элементе цепи.

Активная мощность, потребляемая сопротивлениями R₁ и R₃ :

P:= (| I ₁ |)²∙R₁ +(| I ₃|)²∙R₃ P = 140.516 Bт

Реактивная мощность, запасаемая в индуктивности L₃ и в емкостях C₁ и C₂:

Q:= -(| I ₁|)²∙X_C1-(| I ₂|)²∙X_C2 +[(| I ₃|)²∙X_L3] Q = -209.080 вар

S ₁ := P+jQ S ₁ =140.516 - 209.080j BA

Отдаваемая S и потребляемая S ₁ мощности должны быть равны,

т.е. S – S ₁ = 0.

Баланс мощности сходится. Расчет токов и напряжений выполнен верно.

5. Для проверки правильности вычислений по взаимному расположению векторов токов и напряжений строим для каждой ветви векторы токов и напряжений

Взаимное расположение векторов токов и напряжений должно соответствовать активному или реактивному характеру сопротивления ветви:   - ток первой ветви должен опережать приложенное к Z ₁ = R₁ - j∙X_C1 напряжение на угол ffi(I ₁, U _Z1)= 39.789⁰;   - ток второй ветви должен опережать приложенное к Z ₂ = -j∙X_C2 напряжение на угол 90⁰;   - ток третьей ветви должен отставать от приложенного к Z ₃ = R₃ + j∙X_L3 напряжение на угол ffi(I ₃, U _Z3)= -56.173;   - ток через источник ЭДС Е должен опережать исходное напряжение ЭДС на угол ffi(I ₁,E)= 56.096.

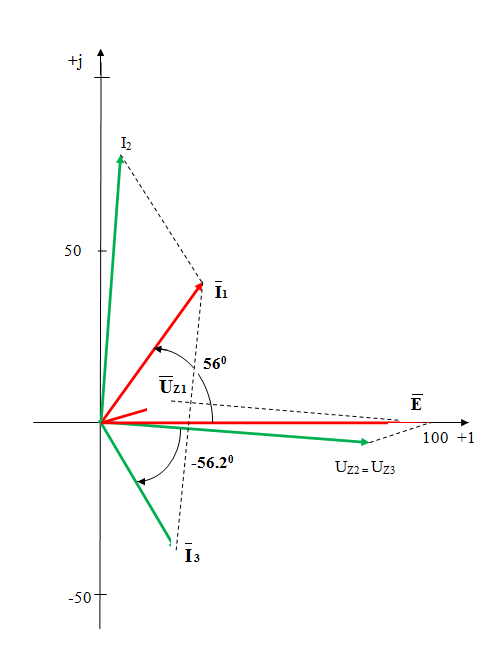
Рис. 2.5. Взаимное расположение векторов токов и напряжений

Дата добавления: 2015-10-16