
Читайте также:
|
Размечаем оси координат Рпс- φ1, причем ось φ1 выбираем горизонтально, а ось Pпс - перпендикулярно к ней. В соответствии с заданием строим диаграмму нагрузок.
По построенным планам скоростей определяем величины скоростей центров масс Vs2, Vs3, Vs5=VE и угловые скорости звеньев - ω2 и ω3 (см. табл. 1.1).
Помимо силы Pпс будем учитывать при расчете Mпр также силы веса звеньев. Для этого на планах скоростей замеряем углы между направлением скоростей центров масс и направлением сил тяжести (вертикалью).
Рассчитываем приведенный момент сил сопротивления по формуле
Mпр = -(Pпс·Vs5·cosα'5+G5·Vs5·cosα5+G3·Vs3·cosα3+G2·Vs2·cosα2)/ω1,
где αi- угол между направлением силы Gi и скорости Vsi. Значение силы сопротивления определяем по графику зависимости силы производственных сопротивлений от угла поворота входного звена. Например, для положения 2 (90˚)
Mпр = -(Pпс·Vs5·cosα'5+G5·Vs5·cosα5+G3·Vs3·cosα3+G2·Vs2·cosα2)/ω1=
= -(450·3,57·cos 180+78,5·3,57·cos0+58,9·3,36·cos178,68
+49,0·10,24·cos172,88/70=28,89 Нм
Для других положений механизма вычисления аналогичны. Результаты расчетов сведены в таблицу 3.1.
Таблица 3.1 Значения приведенного момента сил сопротивлений
и приведенного момента инерции
| По-ло-же-ние | φ1, рад | Углы, град | Приведенные характеристики | ||||
| α2 | α3 | α5 | α'5 | Мпр, Нм | Jпр, кгм2 | ||
| 82,23 | -0,4974 | 0,33185 | |||||
| π/4 | 144,86 | 173,14 | 17,0171 | 0,367 | |||
| π/2 | 172,88 | 178,68 | 28,892 | 0,448 | |||
| 3π/4 | 168,1 | 168,5 | 25,787 | 0,421 | |||
| π | 163,07 | 2,647 | 0,332 | ||||
| крх | 102,7 | 0,809 | 0,332 | ||||
| 5π/4 | 38,62 | 12,97 | -3,795 | 0,40304 | |||
| 3π/2 | 7,72 | 2,97 | -6,146 | 0,465 | |||
| 7π/4 | 21,93 | 6,45 | -4,757 | 0,396 |
Выбрав масштабный коэффициент μM = 0,308Нм/мм, строим график зависимости Мпр(φ1).
Путем графического интегрирования [3] зависимости Мпр(φ1) получаем график работы сил сопротивления Aс(φ1).
Масштабный коэффициент этого графика
μA = μM·μφ·H = 0,308·0.032725·40 = 0,398 Дж/мм,
где μφ = 0.032725 рад/мм - масштабный коэффициент по оси φ1, Н = 40 мм - полюсное расстояние при интегрировании.
Приняв момент движущих сил постоянным, строим график работы движущих сил Aдв(φ1) путем соединения конца графика Aс(φ1) с началом координат.
Путем графического вычитания получаем график изменения кинетической энергии механизма ΔE = Aдв - Aс. Масштабный коэффициент этого графика примемμЕ = 0.398Дж/мм.
Приведенный момент инерции механизма определим по формуле
Jпр = Js1+ Js2(ω2/ω1)2+ m2(Vs2/ω1)2++ Js3(ω3/ω1)2+m3(Vs3/ω1)2+ m5(Vs5/ω1)2.
Например, для положения 2(φ1=90˚):
Jпр =Js1+ Js2(ω2/ω1)2+m2(Vs2/ω1)2+ Js3(ω3/ω1)2 + m3(Vs3/ω1)2+ m5(Vs5/ω1)2=
= 0,3+0,07(3,2/70)2 +5,0(10,24/70)2 + 0,12·(15,54/70)2 +6,0·(3,36/70)2 + +8,0·(3,57/70)2 = 0,448кг·м2
Результаты вычисления Jпр для других положений механизма сведены в таблицу 3.1.
По полученным данным строим график приведенного момента инерции механизма Jпр(φ1) в масштабе μJ= 0,0045 кг·м2/мм, располагая ось φ1 вертикально для удобства последующих построений.
Строим диаграмму Виттенбауэра ΔE(Jпр). Для этого графически исключаем параметр φ1 из графиков ΔE(φ1) и Jпр(φ1): для каждой точки диаграммы энергомасс значение абсциссы берем с графика Jпр(φ1), а значение ординаты - с графика ΔE(φ1) при одном и том же значении угла φ1.
Для определения момента инерции маховика к диаграмме Виттенбауэра проводим касательные под углами ψmax и ψmin. Значения углов рассчитываем по формулам
ψmax = arctg[μJ·(1+δ)·ω12/(2·μЕ)] = arctg[0,0045·(1+0.06)·702/(2·0,398)] =
= 88,0˚,
ψmin = arctg[μJ (1-δ)·ω12/(2·μЕ)] = arctg[0,0045·(1-0.06)·702/(2·0,398)]=
=87,8˚,
где δ = 0.06 - заданный коэффициент неравномерности движения механизма.
Касательные отсекают по оси абсцисс диаграммы отрезки ОА=70,96 мм и ОВ=101,63мм. По этим значениям рассчитаем момент инерции маховика
Jм = (ОВ·tgψmin - ОA·tgψmax)·μЕ/(δ·ω12) =
= (101,63·26,04–70,96,0·28,64)·0,398/(0.06·702) = 0,831 кг·м2
Выполним маховик в виде диска. Тогда [1]:
R = [(2 Jм)/(πρq)]0.2 = [(2·0,831)/(π·7860·0.4)]0.2 = 0.176 м,
где R - радиус диска, q = h/R - отношение толщины диска к радиусу, ρ - плотность материала маховика.
Задаемся q = 0.4, ρ = 7860 кг/м3 (выбираем материал маховика - сталь).
Толщина диска маховика b = 0.4·0.176 = 0.07м.
По рассчитанным размерам строим эскиз маховика.
4. ПРОЕКТИРОВАНИЕ ЗУБЧАТЫХ ПЕРЕДАЧ
4.1. Проектирование прямозубой эвольвентной передачи
Для проектирования заданными являются числа зубьев колес z1=12, z2=20 и модуль m=8,0 мм. Так, как z1‹zmin=17, шестерню необходимо нарезать со смещением инструмента, чтобы обеспечить приемлемые эксплуатационные характеристики передачи.
По блокирующему контуру [4] для передачи, составленной из зубчатых колес с заданными числами зубьев, определяем коэффициенты смещения x1=0,49, x2 = 0,32
4.1.1. Геометрический расчет передачи
Выполняем геометрический расчет передачи по методике, изложенной в [4]. Определяем коэффициент суммы смещений
ХΣ = х1 + х2 = 0,49 + 0,32=0,81
и определяем угол зацепления αw
inv αw = (2· ХΣ ·tgα)/(z1+ z2) + invα;
inv αw = (2·0,81·tg20˚)/(12+ 20) + inv20˚ = 0,03333
Значение αw определяем по значению эвольвентной функции из таблиц:
αw = 25,85˚
Делительное межосевое расстояние
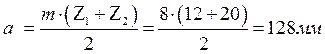
Межосевое расстояние
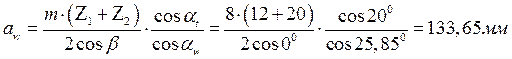
Рассчитываем диаметры зубчатых колес.
Делительные диаметры
d1 = m·z1 = 8,0·12 = 96 мм
d2 = m·z2 = 8,0·20 = 160 мм
Передаточное число
u12 = z2 / z1 = 20/12 = 1,667
Начальные диаметры
dw1 = 2аw/(u + 1) = 2·133,65/(1,667+1) = 100,24 мм
dw2 =2аwu12/(u + 1) = 2·135,65·1,667/(1,667+1) = 167,07 мм
Коэффициент воспринимаемого смещения
y = (аw - а)/m = (133,65 – 128)/8,0 = 0,707
Коэффициент уравнительного смещения
Δy = ХΣ - y = 0,81 – 0,707= 0,103
Диаметры вершин зубьев
da1 = d1 + 2m(hа*+ х1 - Δy) = 96 + 2·8,0·(1 + 0,49–0,103) = 118,19 мм
da2 = d2 + 2m(hа* + х2 - Δy) = 160 + 2·8,0·(1 + 0,32 - 0,103) = 179,47мм
Диаметры впадин зубьев
df1 = d1 - 2m(hа* + c* - х1) = 96- 2·8,0·(1 + 0.25 – 0,49) = 83,84 мм
df2 = d2 - 2m(hа* + c* - х2) = 160 - 2·8,0·(1 + 0.25 – 0,32) = 147,84 мм
Основные диаметры
db1 = d1cosα = 96·cos20˚ = 90,21 мм
db2 = d2cosα = 160·cos20˚ = 150,35 мм
Нормальная толщина (по дуге делительной окружности) определяется как
Sn1 = m(π/2 + 2х1tgα) =8,0 ·(π/2 + 2·0,49 ·tg20˚) = 15,42 мм
Sn2 = m(π/2 + 2х2tgα) =8,0·(π/2 + 2·0,32·tg20˚) = 14,43 мм
Для зубчатых колес с положительным смещением необходимо проверять условие отсутствия заострения зуба, т.е. условие Sa> 0.2m.
Толщина зуба по дуге окружности вершин корригированной шестерни 1 определяется по формуле
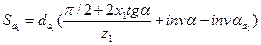
Sа1 = 118,19·[(π/2 + 2·0,49·tg20˚)/12 + inv20˚ - inv40,246˚] = 3,72 мм
где αа1 - угол профиля в точке на концентрической окружности диаметром dа1, рассчитывается как
соs αа1 = (d/dа1)cosα= (96/118,19)cos20˚ = 0,763;
αа1 = 40,246˚
Так как Sа1= 3,72 мм > 0.2m=0.2·8,0= 1,6 мм,то заострения корригированной шестерни 1 нет.
Толщина зуба по дуге окружности вершин корригированногоколеса2 определяется по формуле
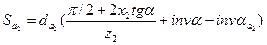

Sа2 = 179,47·[(π/2 + 2·0,32·tg20˚)/20 + inv20˚ - inv33,096˚] = 5,55 мм
где αа2 - угол профиля в точке на концентрической окружности диаметром dа2, рассчитывается как
соs αа2 = (d/dа2)cosα= (160/179,47)cos20˚ = 0,838;
αа2 = 33,096˚
Так как Sа2= 5,55 мм > 0.2m=0.2·8,0= 1,6 мм,то заострения корригированногоколеса2 нет.
Шаг зацепления по основной окружности (основной шаг) определяетсяпо зависимости
pα = π·m·cosα = π·8,0·cos20˚ = 23,62 мм
4.1.2. Построение картины зацепления
Проводим линию центров и в масштабе 0,364 мм/мм откладываем межосевое расстояние аw = 133,65 мм. Из центров вращения шестерни О1 и колеса О2 проводим окружности: начальные, основные, делительные, вершин и впадин зубьев.
Проводим общую касательную к основным окружностям - линию зацепления. Она проходит через точку касания начальных окружностей - полюс зацепления Р, что косвенно свидетельствует о правильности расчетов.
На основных окружностях строим эвольвенты. Для этого откладываем ряд одинаковых дуг и в точках деления проводим касательные. Вдоль касательных откладываем отрезки, равные длинам дуг разбиения. Полученные точки лежат на эвольвентах. Отложив по делительным окружностям нормальные толщины зубьев и отобразив симметрично эвольвенты, выстраиваем полный профиль зубьев. Выполняем шаблоны зубьев колес.
Строим картину пары зубьев, зацепляющихся в полюсе, а затем, откладывая по основным окружностям основной шаг, выстраиваем еще по паре зубьев.
Точки пересечения окружностей вершин с теоретической линией зацепления дают отрезок аb - рабочий участок линии зацепления.
4.1.3. Расчет эксплуатационных характеристик передачи
Коэффициент перекрытия определим по формуле
ε = ab/(π·m·cosα) = 28,93/(π·8,0·cos20˚) = 1,224,
где ab = 28,93 мм - длина рабочего участка линии зацепления с учетом масштаба построения.
Значение коэффициента торцового перекрытия показывает, что передача работает плавно (т.к. ε> 1.05).
Коэффициенты удельных скольжений рассчитываем по формулам
λ12 = 1 - (АВ - X)/(X·u12)
λ21 = 1 - (X·u12)/(АВ - X),
где АВ = 160,26 мм - длина теоретического участка линии зацепления без учета масштаба, Х - переменное расстояние от начала теоретического участка линии зацепления (точки А) до точки, в которой определяется коэффициент. Расчетные данные сводим в таблицу 4.1.
Таблица 4.1. Значения коэффициентов удельных скольжений
| Х, мм | 25,51 | 37,04 | 48,56 | АP=60,09 | 75,06 | 90,03 | 104,99 | 160,26 | |
| λ12 | - ∞ | -2,169 | -0,996 | -0,38 | 0,31 | 0,53 | 0,68 | ||
| λ21 | 0,68 | 0,499 | 0,28 | -0,47 | -1,14 | -2,17 | - ∞ |
По рассчитанным данным строим график удельных скольжений, приняв масштаб 0.025 1/мм.
4.2. Проектирование планетарного механизма
Для привода механизма выбираем двигатель с рабочей частотой вращения 3500 об/мин (ωдв = πn/30 = π·3500/30 = 366.521/с). Привод, состоящий из открытой зубчатой передачи с заданными числами зубьев 12 и 20 и одноступенчатого планетарного редуктора, обеспечивает вращение входного кривошипа механизма с угловой скоростью 701/с.
Потребное передаточное число планетарного редуктора определим
iред = z1ωдв / (z2ω1) = (12·366.52)/(20·70) = 3,142
Выбираем схему планетарного редуктора и подбираем числа зубьев колес этого редуктора для обеспечения передаточного отношения iред= 3,142.
Принимаем z3 = 43 из условия подрезания зуба
Рассчитываем число зубьев опорного колеса 3
Z5= (u3Н-1) z3 =(3,142-1)43 = 92,1
Условие отсутствия заклинивания для внутреннего зацепления (z5>85),
Принимаем число z5 =93 одинаковой чётности. Из условия соосности получаем: z4 = (z5 – z3)/2= (93-43) / 2 =25
Таким образом получаем z3 =43, z4 =25, z5 =93
Из условия соседства число сателлитов не должно превышать К, где
К = 180˚/[arcsin((z4+2)/(z3+z4))].
К=180˚/[arcsin((25+2)/(43+25))]=7,69
Принимаем число сателлитов равным 3, т.е. К =3, и проверяем условие сборки
С = (z3 + z5)/К = (43 + 93)/3 = 45
Поскольку С = 45 - целое число, то механизм может быть собран без натягов.
Проверяем условие обеспечения заданного передаточного отношения
U3Н = 1+ z5 /z3 = 1 + 93/43= 3,163
Отклонение передаточного отношения составляет 0.06%, что допустимо, поэтому принимаем z3 = 43, z4 = 25, z5 = 93.
Приняв модуль m =3,0 мм, строим кинематическую схему планетарного редуктора на листе.
На схеме планетарного редуктора строим треугольник скоростей. По треугольнику скоростей определяем передаточное отношение редуктора.
Скорость точки А
VA= ωдв(mz3)/2 = 366,52·(3·43)/2 = 23640 мм/с = 23,64 м/с
На чертеже скорость т.А изображаем вектором длиной 100 мм. В полученном масштабе скорость точки В по треугольнику скоростей получаем в виде вектора длиной 50 мм. Тогда скорость точки В
VВ = (23,64/100)·50 = 11,82 м/с = 11820,0 мм/с,
а угловая скорость вала водила
ωН = VВ/(m(z3+z4)/2) = 11820,0/(3·(43+25)/2) = 115,882 1/с
Передаточное отношение редуктора по построению
iред = ωдв/ωН = 366,52/115,882 = 3,163
ω1 =115,882/1,667=69,51
Выводы
В результате курсового проектирования был спроектирован механизм долбежного станка
На первом этапе курсового проектирования построена кинематическая схема в восьми положениях. Для каждого положения построен план скоростей, для холостого и рабочего хода построен план ускорений, построены кинематические диаграммы выходного звена.
На втором листе произведен кинетостатический расчет механизма, определены реакции в кинематических парах и уравновешивающая сила (методом планов и с помощью рычага Жуковского)
На третьем листе курсового проекта проведен динамический синтез механизма, построены графики изменения приведенного момента инерции и приведенного момента сил сопротивления в зависимости от угла поворота начального звена. Построена диаграмма Виттенбауэра и определены основные размеры маховика для обеспечения заданного коэффициента неравномерности.
На четвертом листе я построена картина эвольвентного зацепления, построен график удельного скольжения, произведен расчет планетарного механизма.
Дата добавления: 2015-10-16; просмотров: 141 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СИЛОВОЙ РАСЧЕТ РЫЧАЖНОГО МЕХАНИЗМА | | | Строение легких |