Указания к решению задач по механике

Кинематические задачи в случае прямолинейного равнопеременного движения материальной точки решаются, как правило, векторным или координатным способами с помощью двух уравнений для скорости и радиуса-вектора точки в момент времени :

			(1)
			(2)

где 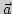- постоянное по величине и направлению ускорение, - начальная скорость, - скорость в момент времени , 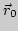- радиус-вектор точки в начальный момент времени при , - радиус-вектор в момент времени .

Выражения (1) и (2) получаются при решении дифференциальных уравнений для мгновенного ускорения и мгновенной скорости:

с учетом начальных условий и при постоянном .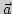

Принцип независимости движений позволяет применять выражения (1) и (2) для и и в случае так называемого баллистического движения, то есть для криволинейного движения тел, брошенных горизонтально и под углом к горизонту.

При решении задач нужно перейти к скалярной форме уравнений (1) и (2), то есть записать каждое из них в проекциях на ось при прямолинейном движении и отдельно в проекциях на ос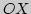и и при криволинейном. При этом следует учесть знаки проекций, а символы векторов опустить. Следует иметь в виду, что проекции радиуса-вектора на оси равны соответствующим координатам материальной точки: , , , . Из системы скалярных уравнений выражаются искомые величины.

Важным этапом решения задач является выбор системы отсчета. При выборе инерциальной системы отсчета необходимо:

1. указать тело отсчета, неподвижное относительно Земли, или поверхность Земли;

2. связать с ним координатные оси и произвольно выбрать их положительное направление;

3. указать положение рассматриваемого тела (тел) в начальный момент времени.

Примечание. В ряде задач на прямолинейное равнопеременное движение в одном направлении применяется "естественный" метод решения, основанный на использовании скалярных величин: траектории движения, пути, модулей средней скорости и среднего ускорения. В этом случае из известных соотношений:

			(3)
			(4)
			(5)

где 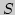- путь, пройденный за время , - средняя скорость, и 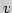- начальная и конечная скорости точки, - среднее ускорение, подставляя в (3) и из (4) и (5), можно получить полезное соотношение:

(6)

которое в частном случае равнопеременного движения без начальной скорости упрощается:

(7)

В случае равнозамедленного движения с нулевой конечной скоростью оно принимает вид:

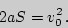
(8)

Подобное соотношение можно получить и из закона сохранения механической энергии материальной точки: если действуют только консервативные силы, например, сила тяжести, потенциальная энергия тела переходит в кинетическую и наоборот:

где 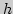- высота, 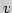- скорость, - ускорение свободного падения, - масса.

Дата добавления: 2015-10-16