
|
Читайте также: |
1.1Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …




1.2 Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …




1.3 Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …




1.4 Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …




1.5 Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
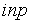



1.6 Установите соответствие между матрицей и ее определителем.
1. 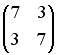
2. 
3. 
- 21
- 42
1.7 Установите соответствие между матрицей и ее определителем.
1. 
2. 
3. 
- 4
- 600
- 28
1.8 Установите соответствие между матрицей и ее определителем.
1. 
2. 
3. 
- 400
- 200
1.9 Установите соответствие между  и значениями определителей
и значениями определителей  .
.
1. 
2. 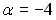
3. 
4. 



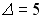


1.11 Установите соответствие между  и значениями определителей
и значениями определителей  .
.
1. 
2. 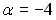
3. 
4. 




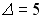
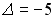
2.1 Вычислите сумму элементов первого столбца матрицы  , если
, если  ,
, 
-6
2.2 Вычислите сумму элементов первого столбца матрицы  , если
, если  ,
, 
-7
2.3 Вычислите сумму элементов первого столбца матрицы  , если
, если  ,
, 
2.4 Вычислите сумму элементов первого столбца матрицы  , если
, если  ,
, 
-16
2.5 Вычислите сумму элементов первого столбца матрицы  , если
, если  ,
, 
-34
2.6 Если  и
и  , то матрица
, то матрица  имеет вид…
имеет вид…




2.7 Если  и
и  , то матрица
, то матрица  имеет вид…
имеет вид…


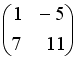

2.8 Если  и
и 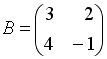 , то матрица
, то матрица  имеет вид…
имеет вид…
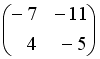



2.9 Даны матрицы  и
и  . Тогда решением матричного уравнения
. Тогда решением матричного уравнения 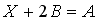 является матрица …
является матрица …

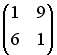


2.10 Даны матрицы  и
и  . Тогда матрица
. Тогда матрица  , являющаяся решением уравнения
, являющаяся решением уравнения  , равна …
, равна …




3.1 Даны матрицы 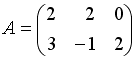 и
и  . Сумма элементов матрицы
. Сумма элементов матрицы  , расположенных на ее главной диагонали, равна …
, расположенных на ее главной диагонали, равна …
3.2 Даны матрицы  и
и  . Сумма элементов матрицы
. Сумма элементов матрицы  равна …
равна …
3.3 Даны матрицы  и
и  . Сумма элементов матрицы
. Сумма элементов матрицы  , расположенных на ее главной диагонали, равна …
, расположенных на ее главной диагонали, равна …
3.4 Даны матрицы 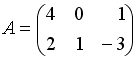 и
и 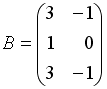 . Сумма элементов матрицы
. Сумма элементов матрицы  , расположенных на ее главной диагонали, равна …
, расположенных на ее главной диагонали, равна …
3.5 Даны матрицы  и
и  . Сумма элементов матрицы
. Сумма элементов матрицы  , расположенных на ее главной диагонали, равна …
, расположенных на ее главной диагонали, равна …
-4
3.6 Даны две матрицы:  и
и  . Элемент первой строки второго столбца произведения
. Элемент первой строки второго столбца произведения  равен
равен

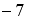
3.7 Даны матрицы  и
и  . Тогда произведение
. Тогда произведение  равно …
равно …




3.8 Для матриц А и В найдено произведение  , причем
, причем  . Тогда матрицей В может быть матрица …
. Тогда матрицей В может быть матрица …




3.9 Заданы матрицы  ,
,  . Тогда элемент
. Тогда элемент  матрицы
матрицы  равен …
равен …
− 10
3.10 Дана матрица  . Тогда матрица
. Тогда матрица 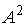 имеет вид …
имеет вид …




4.1 При решении системы линейных уравнений с квадратной матрицей коэффициентов  можно применять формулы Крамера, если
можно применять формулы Крамера, если
один из столбцов матрицы  является линейной комбинацией остальных
является линейной комбинацией остальных
столбцы матрицы  линейно независимы
линейно независимы
определитель матрицы  не равен нулю
не равен нулю
строки матрицы  линейно зависимы
линейно зависимы
4.2 При решении системы линейных уравнений с квадратной матрицей коэффициентов  можно применять формулы Крамера, если
можно применять формулы Крамера, если
строки матрицы  линейно независимы
линейно независимы
определитель матрицы  не равен нулю
не равен нулю
столбцы матрицы  линейно зависимы
линейно зависимы
одна из строк матрицы  является линейной комбинацией остальных
является линейной комбинацией остальных
4.3 При решении системы линейных уравнений с квадратной матрицей коэффициентов  нельзя применять формулы Крамера, если
нельзя применять формулы Крамера, если
определитель матрицы  равен нулю
равен нулю
строки матрицы  линейно независимы
линейно независимы
ни один из столбцов матрицы  не является линейной комбинацией остальных
не является линейной комбинацией остальных
столбцы матрицы  линейно зависимы
линейно зависимы
4.4 При решении системы линейных уравнений с квадратной матрицей коэффициентов  нельзя применять формулы Крамера, если
нельзя применять формулы Крамера, если
ни одна из строк матрицы  не является линейной комбинацией остальных
не является линейной комбинацией остальных
столбцы матрицы  линейно независимы
линейно независимы
строки матрицы  линейно зависимы
линейно зависимы
определитель матрицы  равен нулю
равен нулю
4 5 При решении системы линейных уравнений с квадратной матрицей коэффициентов  нельзя применять формулы Крамера, если
нельзя применять формулы Крамера, если
определитель матрицы  равен нулю
равен нулю
столбцы матрицы  линейно независимы
линейно независимы
строки матрицы  линейно независимы
линейно независимы
ранг матрицы  не равен числу ее уравнений
не равен числу ее уравнений
4.6 Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
1. 
2. 
3. 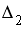
- 2
4 7.Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
1. 
2. 
3. 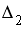
- 5
4.8 Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
1. 
2. 
3. 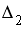
- 17
4.9 Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
1. 
2. 
3. 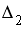
- 3
4 10.Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
1. 
2. 
3. 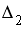
- 4
- 19
5.1 Расположите по возрастанию длины сторон треугольника  , где
, где 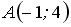 ,
,  и
и 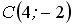 .
.



5.2 Расположите по возрастанию длины сторон треугольника  , где
, где  ,
,  и
и  .
.



5.3 Расположите по возрастанию длины сторон треугольника  , где
, где  ,
,  и
и 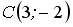 .
.



5.4 Расположите по возрастанию длины сторон треугольника  , где
, где  ,
,  и
и 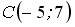 .
.



5.5 Расположите по возрастанию длины сторон треугольника  , где
, где  ,
,  и
и 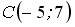 .
.



5.6 Даны точки  ,
,  и
и  . Установите соответствие между отрезком и его длиной.
. Установите соответствие между отрезком и его длиной.
1. 
2. 
3. 
5.7 Установите соответствие между элементами двух множеств ( - расстояние между точками А и В)
- расстояние между точками А и В)
1. 
2. 
3. 

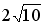
5.8 Установите соответствие между элементами двух множеств ( - расстояние между точками А и В)
- расстояние между точками А и В)
1. 
2. 
3. 


5.9 Установите соответствие между элементами двух множеств ( - расстояние между точками А и В)
- расстояние между точками А и В)
1. 
2. 
3. 
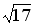

5.10 Установите соответствие между элементами двух множеств ( - расстояние между точками А и В)
- расстояние между точками А и В)
1. 
2. 
3. 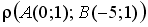
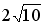

6.1 Даны графики прямых  :
:

Тогда сумма их угловых коэффициентов равна…
6.2 Даны графики прямых 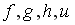 :
:

Тогда сумма их угловых коэффициентов равна…
6.3 Даны графики прямых 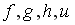 :
:

Тогда сумма их угловых коэффициентов равна…
6.4 Даны графики прямых 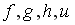 :
:

Тогда сумма их угловых коэффициентов равна…
6.5 Даны графики прямых 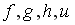 :
:

Тогда сумма их угловых коэффициентов равна…
6.6 Даны вершины треугольника  . Тогда уравнение высоты
. Тогда уравнение высоты  имеет вид …
имеет вид …



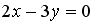
6.7 Выберите уравнение прямой, соответствующее данному рисунку.





6.8Выберите уравнение прямой, соответствующее данному рисунку.





6.9 Прямая проходит через точки 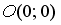 и
и  . Тогда ее угловой коэффициент равен…
. Тогда ее угловой коэффициент равен…


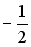

6.10 Уравнением прямой, параллельной  , является …
, является …

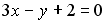


7.1 Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 
2. 
3. 
4. 
гипербола
парабола
окружность
эллипс
7.2 Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 
2. 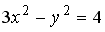
3. 
4. 
эллипс
парабола
окружность
гипербола
7.3 Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 
2. 
3. 
4. 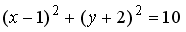
эллипс
гипербола
окружность
парабола
7.4 Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 
2. 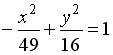
3. 
4. 
окружность
парабола
эллипс
гипербола
7.5 Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 
2. 
3. 
4. 
эллипс
парабола
гипербола
окружность
7.6 Расстояние между фокусами эллипса  равно …
равно …
7.7 Расстояние между фокусами гиперболы  равно …
равно …
7.8 Вещественная полуось гиперболы, заданной уравнением  , равна…
, равна…
7.9 Малая полуось эллипса, заданного уравнением  , равна…
, равна…
7.10 Большая полуось эллипса, заданного уравнением  , равна…
, равна…
8.1 Нормальный вектор плоскости 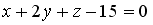 имеет координаты…
имеет координаты…
(1; 1; – 15)
(1; 2; – 15)
(1; 2; 1)
(2; 1; – 15)
8.2 Нормальный вектор плоскости  имеет координаты…
имеет координаты…
(1; – 9; – 17)
(1; 5; – 9)
(5; – 9; – 17)
(– 1; – 5; 9)
8.3 Прямая  пересекает плоскость
пересекает плоскость  только в том случае, когда
только в том случае, когда  не равно …
не равно …

8.4 Уравнение плоскости, проходящей через точку  и параллельной плоскости
и параллельной плоскости 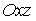 , имеет вид …
, имеет вид …



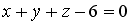
8.5 Уравнение плоскости, проходящей через точку  и параллельной плоскости
и параллельной плоскости 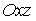 , имеет вид …
, имеет вид …

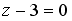


8.6 Установите соответствие между уравнением плоскости и ее положением в пространстве
1. 
2. 
3. 
4. 
проходит через ось y
параллельна оси 
проходит через начало координат
параллельна оси 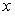
параллельна оси 
8.7 Установите соответствие между уравнением плоскости и ее положением в пространстве
1. 
2. 
3. 
4. 
проходит через начало координат
параллельна оси 
параллельна оси 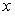
параллельна оси 
проходит через ось 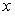
8.8 Установите соответствие между уравнением плоскости и точками, которые лежат в этих плоскостях
1. 
2. 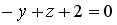
3. 
4. 





8.9 Установите соответствие между уравнением плоскости и точками, которые лежат в этих плоскостях
1. 
2. 
3. 
4. 





8.10 Установите соответствие между уравнением плоскости и точками, которые лежат в этих плоскостях
1. 
2. 
3. 
4. 





Вопросы для подготовки к экзамену
1. Матрицы. Операции над матрицами.
2. Определители. Миноры и алгебраические дополнения. Теорема Лапласа.
3. Свойства определителей.
4. Обратная матрица. Теорема о существовании. Алгоритм вычисления.
5. Ранг матрицы. Элементарные преобразования. Определение ранга матрицы.
6. Линейная зависимость (независимость) и линейная комбинация строк (столбцов) матрицы.
7. Теорема о ранге матрицы.
8. Система линейных уравнений. Матричная запись. Метод обратной матрицы.
9. Метод Крамера решения системы линейных уравнений.
10. Метод Гаусса.
11. Система m линейных уравнений с n переменными.
12. Система линейных однородных уравнений.
13. Фундаментальная система решений.
14. Модель Леонтьева.
15. Метод координат.
16. Вектор. Сложение, вычитание, и умножение на число.
17. Проекция вектора на ось. Свойства.
18. Разложение вектора по базису. Свойства координат вектора.
19. Скалярное произведение. Свойства. Координатная запись.
20. n-мерный вектор и векторное пространство.
21. Размерность и базис векторного пространства.
22. Свойства линейного пространства.
23. Переход к новому базису.
24. Евклидово пространство.
25. Ортонормированный базис.
26. Линейные операторы. Матрица линейного оператора.
27. Алгебраические операции над линейными операторами.
28. Матрица линейного оператора в разных базисах.
29. Собственные векторы и собственные значения линейных операторов.
30. Приведение матрицы линейного оператора к диагональному виду.
31. Квадратичные формы. Матричная запись.
32. Канонический вид квадратичной формы.
33. Знакоопределенность квадратичной формы.
34. Линейная модель обмена.
35. Уравнение линии на плоскости.
36. Уравнения прямой на плоскости.
37. Свойства и условия взаимного расположения прямых, точек и прямых на плоскости.
38. Плоскость и прямая в пространстве.
39. Геометрический смысл неравенств первой степени на плоскости и в пространстве.
40. Кривые 2-го порядка.
41. Кривые эллиптического типа.
42. Кривые гиперболического типа.
43. Кривые параболического типа.
Дата добавления: 2015-10-16; просмотров: 211 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задания для самостоятельной работы. | | | Оформление контрольной работы |