Решение тригонометрических уравнений

Команда solve, примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале от 0 до 2*π.

>solve(sin(x)=cos(x),x);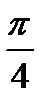

Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true.

Решение простых неравенств

Команда solve применяется также для решения неравенств. Решение неравенства выдается в виде интервала изменения искомой переменной. В том случае, если решение неравенства полуось, то в поле вывода появляется конструкция вида RealRange(–∞, Open(a)), которая означает, что x 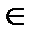(–∞, a), а – некоторое число. Слово Open означает, что интервал с открытой границей. Если этого слова нет, то соответствующая граница интервала включена во множество решений.

Решение систем неравенств

С помощью команды solve можно также решить систему неравенств.

Анализ и решение задач межотраслевого баланса в Maple.

> restart;
> A:= matrix([[.1,.3,.6], [.2,.2,.2], [.3,.1,.1]]);
> Y:= matrix([[25], [36], [54]]);
> E:= matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]]);
> B:= evalm(E-A);
> with(linalg);

> linsolve(B, Y);
> evalf(%, 3);

Анализ и решение задач оптимизации плана производства в Maple.

План:

1. Целевая функция (F:=c1*x1+…+cn*xn)

2. Ограничения (только основные)

3. Подключить одну из библиотек (with(simplex) или with (Optimization))

4. Указать цель задачи: maximize (функция, ограничения)

Анализ и решение задач оптимизации плана транспортных перевозок в Maple.

План:

1. Целевая функция (F:=c1*x1+…+cn*xn)

2. Ограничения (только основные)

3. Подключить одну из библиотек (with(simplex) или with (Optimization))

4. Указать цель задачи: minimize. (функция, ограничения)

Дата добавления: 2015-10-21