Непрерывность функции. Функция f(x) называется непрерывной в точке х0, если

Функция f(x) называется непрерывной в точке х₀, если

.

Если функция f(x) непрерывна в точке х₀, то

f(x) = f(x₀) + α(x),

где α(х) – бесконечно малая при x → x₀.

Все элементарные функции непрерывны в тех точках, в которых они определены.

Точка x = а называется устранимой точкой разрыва, если существует конечный предел в этой точке и .

Точка x = а называется точкой разрыва 1-го рода, если существуют конечные пределы слева и справа и

Точка х = а называется точкой разрыва 2-го рода, если хотя бы один из односторонних пределов равен бесконечности или не существует

Пример 6. Функцию 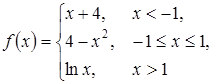исследовать на непрерывность в точках разрыва и определить их тип. Сделать чертеж.

Решение. Достаточно проверить непрерывность этой функции только в точках х₁ = –1 и х₂ = 1.

В точке x₁ = –1

то есть

.

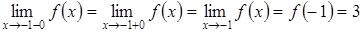Следовательно, функция f(x) непрерывна в точке x₁ = –1.

В точке х₂ = 1

Так как

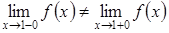
то функция f(x) в точке х₂ =1 имеет разрыв 1-го рода.

Разность f(1+0) – f(1–0) = –3 называется скачком функции в точке разрыва (рис. 1).

Рис. 1.

Дата добавления: 2015-10-21