Предел функции

Методические указания к контрольной работе

ПРЕДЕЛ ФУНКЦИИ. ПРОИЗВОДНАЯ

Предел функции

Число а называется пределом функции f(x) при x ® х₀, если для любого числа e>0 существует такое число d= d(e)>0, что для всех x, удовлетворяющих условию 0<| x – х₀ |<d, выполняется неравенство | f(x) – а | < e. Используется следующее обозначение:

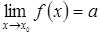
Если рассматриваются только значения x < х₀, то предел

называется пределом слева.

Если рассматриваются только значения x > х₀, то предел

называется пределом справа.

Предел в точке х₀ существует тогда и только тогда, когда существуют пределы слева и справа и они равны.

Число а называется пределом функции f(x) при x ® ¥, если для любого числа e > 0 существует такое число N = N( e ) > 0, что для всех x, удовлетворяющих условию | x |> N, выполняется неравенство | f(x) – а | < e. При этом используется обозначение

Свойства пределов

Предел постоянной равен этой же постоянной:

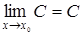, С = const.

Если существуют конечные пределы и , то:

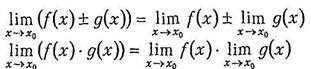
В частности, , где c=const;

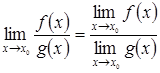
в последнем случае предполагается, что .

Здесь и далее x может стремиться как к конечному числу, так и к бесконечности.

Функция a (x) называется бесконечно малой при x ® х₀, если

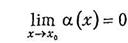
Если 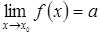, то

f(x) = a + a(x),

где a(x) – бесконечно малая при x ® х₀.

Пусть a (x) и b (x) бесконечно малые при x ® х₀, причем 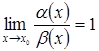, тогда a (x) и b (x) называются эквивалентными бесконечно малыми. Обозначение:

a (x) ~ b (x) при x ® х₀.

Пусть a (x), a₁ (x), b (x), b₁ (x) – бесконечно малые при x ® х₀ и a (x) ~ a₁ (x), и b (x) ~ b₁ (x), тогда

если хотя бы один из этих пределов существует.

Таким образом, при нахождении пределов бесконечно малые можно заменять на эквивалентные им бесконечно малые, более простые.

Часто используются следующие соотношения при x ® х₀:

sin x ~ x, , tg x ~ x, arcsin x ~ x,

arctg x ~ x, e ^x – 1 ~ x, ln(l + x) ~ x.

Первый замечательный предел:

Второй замечательный предел:

где e=2,71828...

Пример 1. Найти .

Решение. Пределы числителя и знаменателя равны бесконечности: имеет место неопределенность вида . Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель дроби на старшую степень x, т.е. на x². После этого можно применить свойство 3 о пределе частного.

.

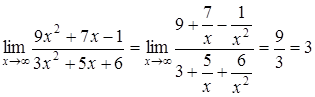Пример 2. Найти .

Решение. В данном случае имеем неопределенность вида . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на выражение, сопряженное числителю, то есть на :

.

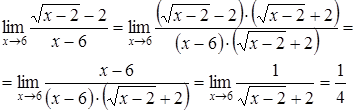Пример 3. Найти .

Решение. Имеем неопределенность вида . В числителе и знаменателе перейдем к эквивалентным бесконечно малым:
arcsin²5 х ~ (5x)², ln(l + 3 x ²) ~ 3х², тогда

.

Пример 4. Найти .

Решение. Неопределенность ∞∙0. Воспользуемся тем, что тем, что при x →∞ и получим:

.

Пример 5. Найти .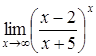

Решение. Неопределенность вида 1^∞. Применим основное логарифмическое тождество e ^{ln N} = N, а потом воспользуемся тем, что при x →∞.

Тогда .

Дата добавления: 2015-10-21