Задача №2. Двум заводам изобретающих мягкие игрушки «Медвежонок»

Двум заводам изобретающих мягкие игрушки «Медвежонок», «Зайчик», необходимо продать партии из 30 и 50 игрушек. Они могут распределить их между 3 магазинам игрушек, «Дом игрушек», «Детский мир», «Карапуз», которым требуются игрушки в количестве 650шт., 500 шт., 450 шт. соответственно. Тарифы перевозок представлены следующей матрице:

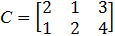
Необходимо найти наиболее выгодный способ распространить партии игрушек между магазинами.

Решение: Опираясь на матрицу тарифов перевозок, составляем уравнение баланса, гарантирующее полное задействование мощностей каждого из производителей:

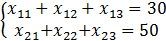
Таким же образом составляем уравнение баланса, гарантирующее удовлетворение спроса всех потребителей:

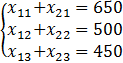
Чтобы предотвратить отрицательность переменных, вводим следующее условие: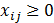

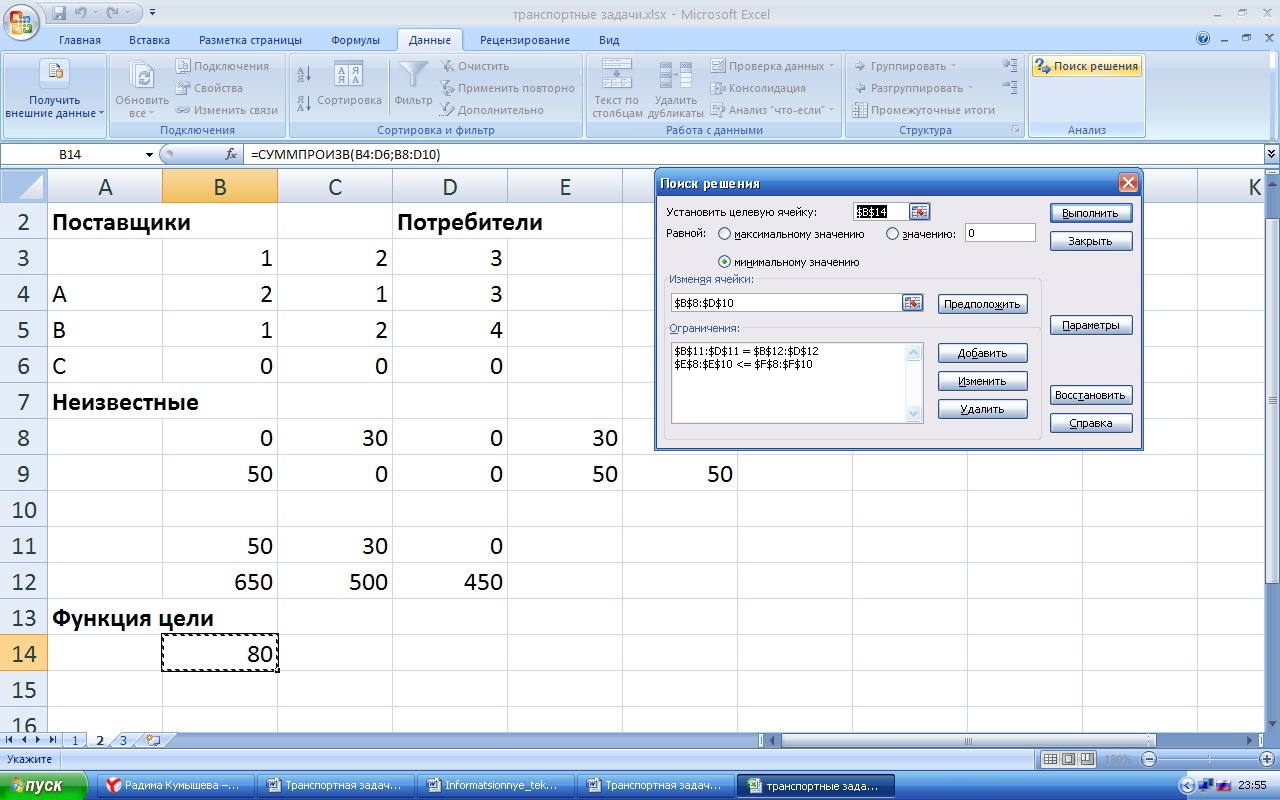
Выражаем суммарные затраты F на перевозку следующим уравнением:

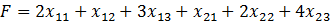
Для математической постановки транспортной задачи в общей постановке обозначим через с_ij коэффициенты затрат, через M_i – мощности поставщиков, через N_j – мощности потребителей, (i=1,2,…,m)., (j=1,2,…,n), m – число поставщиков, n – число потребителей. Тогда система ограничений принимает вид:

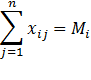
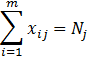
Вводим необходимое условие равенства суммарной мощности поставщиков и потребителей:

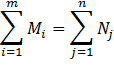
На основе всего этого выводим целевую функцию:

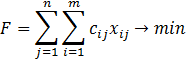
В ячейках E8-E9 помещаются формулы: =СУММ(B8:D8); =СУММ(B9:D9).

В ячейках B11-D11помещаются формулы: =СУММ(B8:B9); =СУММ(C8:C9); =СУММ(D8:D9).

Формула ячейки B14: =СУММПРОИЗВ(B4:D6;B8:D10).

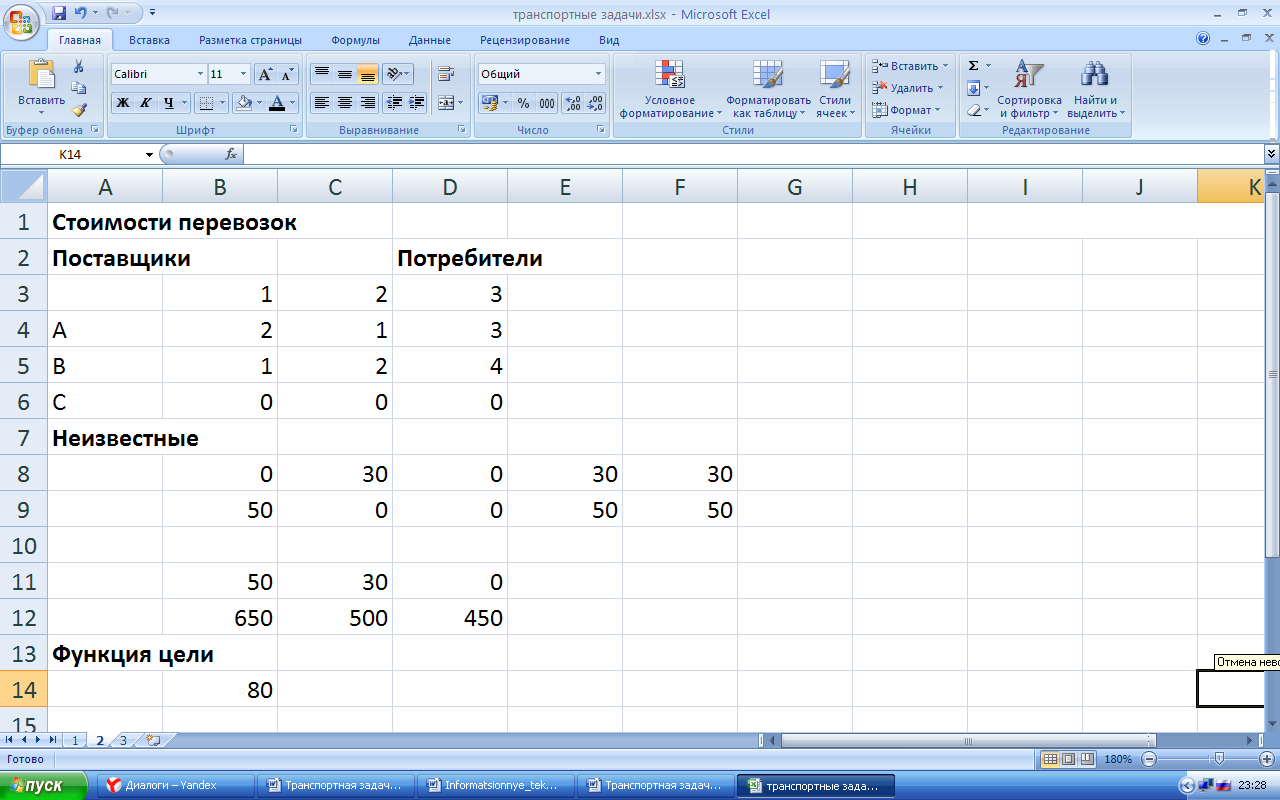
Для решения задачи используем функцию «Поиск решения» данной программы, используя следующие параметры:

Вывод: Таким образом, удалось найти решение, которое полностью удовлетворяет потребности как поставщиков, так и потребителей. Наиболее дешевое распределение товара поставщиков между потребителями обойдется поставщикам в 80 руб.

Дата добавления: 2015-10-13