
Читайте также:
|
367. Дано цілі числа 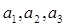 Одержати цілочисельну матрицю
Одержати цілочисельну матрицю 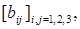 для якої
для якої 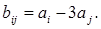
368. Дано дійсні числа 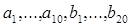 .Одержати дійсну матрицю
.Одержати дійсну матрицю 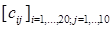 для який
для який 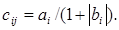
369. Одержати 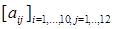 - цілочисельну матрицю, для якої
- цілочисельну матрицю, для якої 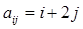
370. Дано натуральне число n. Одержати дійсну матрицю  для якої
для якої
а) 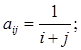
371. Дано дійсну квадратну матрицю  Одержати дві квадратні матриці
Одержати дві квадратні матриці 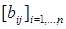
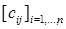 для яких
для яких
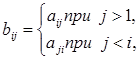
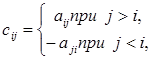
372. Одержати дійсну матрицю  перший рядок якої i задається формулою
перший рядок якої i задається формулою 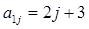 , (j=1,..,7)другий рядок задається формулою
, (j=1,..,7)другий рядок задається формулою 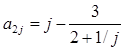 (j=1,…,7), а кожна наступна cтрока сума двох попередніх.
(j=1,…,7), а кожна наступна cтрока сума двох попередніх.
373. Дано натуральне число п, дійсна матриця розмір n  9. Знайти середнє арифметичне:
9. Знайти середнє арифметичне:
а) кожного зі стовпців;
б) кожного зі стовпців, що мають парні номери.
374. Дано натуральне число п. З'ясувати, скільки позитивних елементів містить матриця 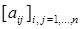 якщо
якщо
a) 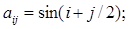
б) 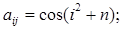
в) 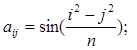
375. Дано дійсну матрицю розміру п  т, у якій не всі елементи дорівнюють нулю. Одержати нову матрицю шляхом розподілу всіх елементів даної матриці на її найбільший по модулі елемент.
т, у якій не всі елементи дорівнюють нулю. Одержати нову матрицю шляхом розподілу всіх елементів даної матриці на її найбільший по модулі елемент.
376. Дано натуральне число т, цілі числа 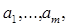 і цiлочисленна квадратна матриця порядку від. Рядок з номером i матриці назвемо відзначеної, якщо а > 0, і невідміченої в противному випадку.
і цiлочисленна квадратна матриця порядку від. Рядок з номером i матриці назвемо відзначеної, якщо а > 0, і невідміченої в противному випадку.
а) Потрібно всі елементи, розташовані у відзначених рядках матриці, перетворити але правилу; негативні елементи замінити на —1, додатні на 1, а нульові залишити без зміни.
б) Підрахувати число негативних елементів матрицю, розташованих у відзначених рядках.
377. Дано дійсну квадратну матрицю порядку 12. Замінити нулями всі її елементи, розташовані на головній діагоналі і вище її.
378. Дано дійсні числа 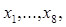 Одержати дійсну квадратну матрицю порядку 8;
Одержати дійсну квадратну матрицю порядку 8;
а)  б)
б) 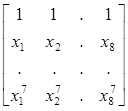
379. Дано дійсну матрицю розміру т  п. Визначити числа
п. Визначити числа 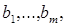 рівні відповідно:
рівні відповідно:
а) сумам елементів рядків;
б) добуткам елементів рядків;
в) найменшим значенням елементів рядків;
г) значенням середніх арифметичних елементів рядків;
д) різницям найбільших і найменших значень елементів рядків.
380. Дано натуральне число n, дійсна матриця 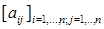 . Одержати послідовність. елементів головної діагоналі
. Одержати послідовність. елементів головної діагоналі 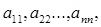
381. Всі елементи з найбільшим, значенням у даної цілочисельній квадратній матриці порядку 10 замінити нулями.
382. Дано дійсну матрицю розміру 6  9. Знайти
9. Знайти
середнє арифметичне найбільшого і найменшого значень її елементів.
383. Дано дійсну матрицю розміру 18  п. Знайти значення найбільшого по модулі елемента матриці,
п. Знайти значення найбільшого по модулі елемента матриці,
а також індекси якого-небудь елемента зі знайденим значенням модуля.
384. Дано дійсну матрицю розміру т  п. Знайти суму найбільших значень елементів її рядків.
п. Знайти суму найбільших значень елементів її рядків.
385. У поданій дійсній квадратній матриці порядку п знайти суму елементів рядка, у якій розташований елемент із найменшим значенням. Передбачається, що такий елемент єдиний.
386. У даній дійсній матриці розміру 6  9 поміняти місцями рядок, що містить елемент із найбільшим значенням, з рядком, що містить елемент із найменшим значенням. Передбачається, що ці елементи єдині.;
9 поміняти місцями рядок, що містить елемент із найбільшим значенням, з рядком, що містить елемент із найменшим значенням. Передбачається, що ці елементи єдині.;
387. Дано натуральне число п, дійсна квадратна матриця порядку п, дійсні 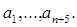 Елементи послідовності
Елементи послідовності 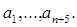 помножить на 10, якщо найбільший елемент матриці (у припущенні, що такий елемент єдиний) знаходите» на головній діагоналі, і на 0.5 у противному випадку.
помножить на 10, якщо найбільший елемент матриці (у припущенні, що такий елемент єдиний) знаходите» на головній діагоналі, і на 0.5 у противному випадку.
388. У даної квадратний цілочисельній матриці порядку 17 вказати індекси всіх елементів з найбільшим
значенням.
389. Дано дійсну матрицю розміру п  т, всі елементи якої різні. У кожнім рядку вибирається елемент із найменшим значенням, потім серед цих чисел вибирається найбільше. Вказати індекси елемента зі знайденим значенням,
т, всі елементи якої різні. У кожнім рядку вибирається елемент із найменшим значенням, потім серед цих чисел вибирається найбільше. Вказати індекси елемента зі знайденим значенням,
390. Дано дійсну матрицю розміру п  т. Одержати послідовність
т. Одержати послідовність 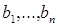 - де
- де 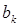 це
це
а) найбільше зі значень елементів k-й рядка;
б) сума найбільшого і найменшого зі значень елементів k-й рядка;
в) число негативних елементів у k-й рядку;
г) добуток квадратів тих елементів k-й рядка, модуль яких належать відрізку [1, 1.5].
391, Дані натуральне число п, цілочисельна матриця 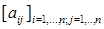 . Знайти суму тих з елементів
. Знайти суму тих з елементів 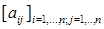 для який a1j має значення найбільшого серед значень
для який a1j має значення найбільшого серед значень 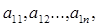
392. Дана цілочисельна квадратна матриця порядку 8. Знайти найменше зі значень елементів стовпця,:, що має найбільшу суму модулів елементів.Якщо таких стовпців трохи, те взяти перший з них.
393. Дано натуральне число п, цілочисельна квадратну матрицю порядку п. Одержати 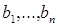 де
де 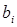 - це
- це
а) найменше зі значень елементів, що знаходяться на початку 1-й рядка матриці до елемента, що належить головної діагоналі, включно;
б) значення першого один по одному позитивного елемента 1-й рядка (якщо таких елементів ні, то прийняти 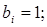 ;
;
в) сума елементів, розташованих за першим негативним елементом у 1-й рядку (якщо всі елементи рядка ненегативні, то прийняти 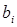 =100);
=100);
г) сума елементів, що передують останньому негативному елементу 1-й рядка (якщо всі елементи рядка ненегативні, то прийняти 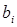 =—1).
=—1).
394. Дана цілочисельна квадратна матриця порядку п. Знайти номера рядків:
а) всі елементи як-нулі;
б) елементи в кожній з який однакові;
в) всі елементи яких парні;
г) елементи кожної з який утворять монотонну
послідовність (монотонно убутну чи монотонно зростаючу);
д) елементи яких утворять симетричні послідовності (паліндроми).,
395. Дано натуральне число п, дійсне число х, дійсна матриця розміру п  2п. Одержати послідовність
2п. Одержати послідовність 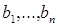 з нулів і одиниць, де
з нулів і одиниць, де 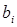 = 1, якщо елементи і-й рядка матриці не перевершують х, і
= 1, якщо елементи і-й рядка матриці не перевершують х, і 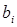 =0 у противному випадку.
=0 у противному випадку.
396. Дано дійсну квадратну матрицю порядку п. Побудувати послідовність дійсних чисел 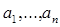 за правилом: якщо в г-й рядку матриці елемент, що належить головної діагоналі, негативний, те а, дорівнює сумі елементів і-й рядка, що передують першому негативному елементу; у противному випадку і, дорівнює сумі останніх елементів і-й рядка, починаючи з першого один по одному ненегативного елемента.
за правилом: якщо в г-й рядку матриці елемент, що належить головної діагоналі, негативний, те а, дорівнює сумі елементів і-й рядка, що передують першому негативному елементу; у противному випадку і, дорівнює сумі останніх елементів і-й рядка, починаючи з першого один по одному ненегативного елемента.
397. Дано дійсну квадратну матрицю порядку 10. У рядках з негативним елементом на головній діагоналі знайти:
а) суму всіх елементів;
б) найбільший із всіх елементів.
398. Дана дійсна квадратна матриця порядку п. Розглянемо ті елементи, що розташовані в рядках, що починаються з негативного елемента. Знайти суми тих з них, що розташовані відповідно нижче, вище і на головній діагоналі.
399. Дана дійсна квадратна матриця порядку 9. Одержати целочисленную квадратну матрицю того ж порядку, в який елемент дорівнює одиниці, якщо елемент який співпадає з вихідної матриці більше елемент що міститься у його рядку на головній діагоналі, і дорівнює нулю в іншому випадку.
400. Дано дійсну квадратну матрицю порядку n.Одержати 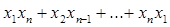 де
де 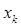 -більше значення елементів k-й рядка даної матриці.
-більше значення елементів k-й рядка даної матриці.
401. Дано дійсну квадратну матрицю порядку п, натуральні числа i, j (1 < i < j < 24). З матриці видалити і-й рядок і j-й стовпець.
402. Дано натуральне число n < 2, дійсна квадратна матриця порядку п. Побудувати послідовність 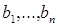 з нулів і одиниць, у якій
з нулів і одиниць, у якій 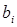 =l тоді і тільки тоді, коли
=l тоді і тільки тоді, коли
а) елементи г-й рядка матриці утворять зростаючу послідовність;
б) елементи 1-й рядка матриці утворять зростаючу чи убутну послідовність.
403. Дана цілочисельена квадратна матриця порядку 15. З'ясувати, чи маються в матриці ненульові елементи, і якщо маються, те вказати індекси:
а) одного з ненульових елементів;
б) усіх ненульових елементів.
404. Дано натуральні числа i, j, дійсна матриця розміру 18  24 (1 < i < j < 24). Поміняти в матриці місцями i-й і j - і стовпці.
24 (1 < i < j < 24). Поміняти в матриці місцями i-й і j - і стовпці.
405. Дано натуральне число п, дійсна квадратна матриця порядку п. Побудувати послідовність 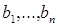 з нулів і одиниць, у якій
з нулів і одиниць, у якій 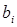 = 1 тоді і тільки тоді, коли в i-й рядку матриці є хоча б один негативний елемент.
= 1 тоді і тільки тоді, коли в i-й рядку матриці є хоча б один негативний елемент.
406. За допомогою 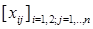 - дійсної матриці на площині задано п крапок так, що
- дійсної матриці на площині задано п крапок так, що 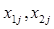 -координати j - і крапки. Крапки попарно з'єднані відрізками. Знайти довжину найбільшого відрізка.
-координати j - і крапки. Крапки попарно з'єднані відрізками. Знайти довжину найбільшого відрізка.
407. Дано натуральні числа п і т, дійсне число r, дійсна матриця розміру n  т. Одержати значення
т. Одержати значення
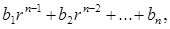
де 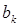 - перший один по одному позитивний елемент у k-й рядку матриці (k = 1,....,n) якщо в k-й рядку немає позитивних елементів, те
- перший один по одному позитивний елемент у k-й рядку матриці (k = 1,....,n) якщо в k-й рядку немає позитивних елементів, те 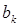 =0.5.
=0.5.
408. Знайти суму квадратів тих елементів 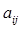 матриці
матриці 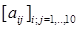 для яких виконано 2 <i < 9,2 <j <9,
для яких виконано 2 <i < 9,2 <j <9, 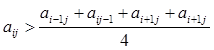
409. Дано дійсну квадратну матрицю порядку 9. Обчислити суму тих з її елементів, розташованих на головній діагоналі і вище її, що перевершують по величині всі елементи, розташовані нижче головної діагоналі. Якщо на головній діагоналі і вище її немає елементів із зазначеною властивістю, то відповіддю повинне служити повідомлення про це.
410. Дана цiлочислена матриця 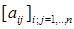 Одержати
Одержати 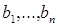 де
де 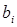 - це
- це
а) 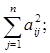 б)
б) 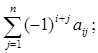
в) 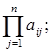 г)
г) 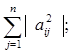
д) 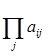 для всех таких j,що 1 <
для всех таких j,що 1 < 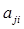 < n
< n
e)max 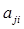 . Min
. Min 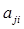 .
.
1<j<n 1<j<n
411. Будемо називати сусідами елемента з індексами i,j деякої матриці такі елементи цієї матриці, що відповідають індекси яких відрізняються від i та j не більше ніж на одиницю. Для даної целочисленной матриці 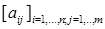 знайти матрицю з нулів і одиниць
знайти матрицю з нулів і одиниць 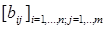 , елемент якої
, елемент якої  дорівнює одиниці, коли
дорівнює одиниці, коли
а) усі сусіди 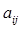 менше самого
менше самого 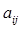 ;
;
б) усі сусіди 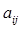 і саме
і саме 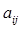 дорівнюють нулю;
дорівнюють нулю;
в) серед сусідів 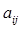 є не менш двох співпадаючих з
є не менш двох співпадаючих з 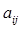 .
.
412. Дано дві цілочисельні квадратні матриці порядку 6. Знайти послідовність з нулів і одиниць 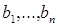 таку, що
таку, що 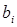 ==1, коли
==1, коли
а) всі елементи і - й рядка першої матриці більше відповідних елементів і - й рядка другої матриці;
б) всі елементи і - е рядків першої і другої матриць негативні;
в) і-й рядка першої і другої матриць містять разом не більш трьох додатних елементи;
г)кількість додатних і ненегативних елементів і-й строки першої матриці збігається відповідно з кількістю негативних і ненегативних елементів і-й рядка другої матриці.
413. Таблиця футбольного чемпіонату задана квадратною матрицею порядку п, у якій всі елементи, що належать головної діагоналі, дорівнюють нулю, а кожен елемент, що не належить головної діагоналі, дорівнює 2, 1 чи 0 (числу окулярів, набраних у грі: 2-виграш, 1-нічия, 0-програш).
а) Знайти число команд, що мають більше перемог, чим поразок.
б) Визначити номера команд, що пройшли чемпіонат без поразок.
в) З'ясувати, чи мається хоча б одна команда, що виграла більш половини ігор.
414. Дано натуральні числа 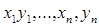 . Числа
. Числа 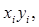 розглядаються як координати і-й крапки (i =1,...,n). Позначимо через
розглядаються як координати і-й крапки (i =1,...,n). Позначимо через 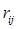 відстань від i-й крапки до j-й. Одержати на екрані задані крапки і з'єднати відрізком і - ю крапку з j-й в тому випадку, якщо виконується принаймні одна умова:
відстань від i-й крапки до j-й. Одержати на екрані задані крапки і з'єднати відрізком і - ю крапку з j-й в тому випадку, якщо виконується принаймні одна умова:
1) 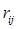 має найбільше значення з
має найбільше значення з 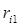 ,
, 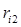 ,…,
,…, 
2) 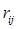 має найбільше значення з
має найбільше значення з 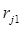 ,
, 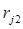 ,…,
,…, 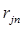
415. Дана целочисленная квадратна матриця порядку га. Кожен елемент • матриці ставиться у відповідність крапці, що належить квадратної області екрана розміром п  п крапок. Лівий верхній кут області має координати 0
п крапок. Лівий верхній кут області має координати 0  0. Відповідність між елементами матриці і крапками області екрана встановлюється в такий спосіб: елемент матриці, що коштує в рядку з номером г i в стовпці з номером j, відповідає крапці екрана, що знаходиться на перетинанні рядка крапок області з номером i і стовпця крапок області з номером j. Думаючи, що кожен елемент матриці задає колір відповідної крапки екрана, одержати на екрані зображення, закодоване, у матриці А.
0. Відповідність між елементами матриці і крапками області екрана встановлюється в такий спосіб: елемент матриці, що коштує в рядку з номером г i в стовпці з номером j, відповідає крапці екрана, що знаходиться на перетинанні рядка крапок області з номером i і стовпця крапок області з номером j. Думаючи, що кожен елемент матриці задає колір відповідної крапки екрана, одержати на екрані зображення, закодоване, у матриці А.
416. Дано дві цілочисельні квадратні матриці порядку п. У кожній з матриць закодоване зображення прямокутної області екрана розміром n  n крапок з координатами лівого верхнього кута 0, 0 (див. попередню задачу). На відміну від попередньої задачі, всі елементи обох матриць - це числа, рівні нулю, якщо крапка складає тло, чи одиниці, якщо частину-точка-частина зображення. Одержати на екрані зображення, що є;
n крапок з координатами лівого верхнього кута 0, 0 (див. попередню задачу). На відміну від попередньої задачі, всі елементи обох матриць - це числа, рівні нулю, якщо крапка складає тло, чи одиниці, якщо частину-точка-частина зображення. Одержати на екрані зображення, що є;
а) перетинанням зображень, закодованих у першій і другій матрицях;
б) об'єднанням зображень, закодованих у першій і другій матрицях.
417. Дано натуральні числа 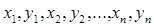 целочисленная матриця
целочисленная матриця 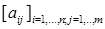 . Послідовність
. Послідовність 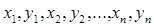 задає координати п крапок. Матриця вказує, як з'єднані між собою крапки:
задає координати п крапок. Матриця вказує, як з'єднані між собою крапки: 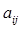 = 1, якщо г-я крапка з'єднана з j-й, та
= 1, якщо г-я крапка з'єднана з j-й, та 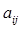 =0 у противному випадку (
=0 у противному випадку (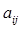 =
= 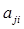 ). Одержати на екрані крапки, задані послідовністю
). Одержати на екрані крапки, задані послідовністю 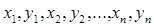 і з'єднати їх між собою так, як зазначено в даній матриці.
і з'єднати їх між собою так, як зазначено в даній матриці.
418. Нехай A1, А2,...- послідовність квадратних матриць з нулів і одиниць така, що порядок матриці Аі; дорівнює 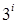
1) 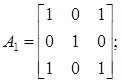
2)при і > 1 має місце
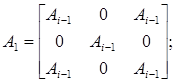
де 0 позначає частина матриці, заповнену нулями.
Дано натуральне число п. Побудувати зображення квадратної області екрана, закодоване в матриці  (див. задачу 415). Лівий верхній кут області повинний збігатися про лівий верхній кут екрана. Випробувати різні способи використання кольору при побудові зображення. Якщо фоновий колір має номер 0, а інші кольори 1,..., k, те при обробці елемента
(див. задачу 415). Лівий верхній кут області повинний збігатися про лівий верхній кут екрана. Випробувати різні способи використання кольору при побудові зображення. Якщо фоновий колір має номер 0, а інші кольори 1,..., k, те при обробці елемента 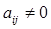 можна, наприклад, брати колір з номером l + 1, де l дорівнює залишку від розподілу
можна, наприклад, брати колір з номером l + 1, де l дорівнює залишку від розподілу 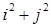 на k, і т.д.
на k, і т.д.
419. Дано символьну квадратну матрицю порядку 10. Замінити буквою а весь її елементи, розташовані вище головної діагоналі.
420. Дано натуральне п, символьна квадратна матриця порядку п. Одержати послідовність 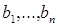 з нулів і одиниць, у якій b = 1 тоді і тільки тоді, коли в i-й рядку число символів * не менше числа пробілів.
з нулів і одиниць, у якій b = 1 тоді і тільки тоді, коли в i-й рядку число символів * не менше числа пробілів.
421. Дано символьну матрицю розміру 13  18. Знайти!
18. Знайти!
а) номер першої один по одному рядка, що містить найбільше число цифр;
б) номер першого один по одному стовпця, що містить I найменше число пробілів на перетинанні з рядками, номера яких парні;
в) номер останньої один по одному рядка, що містить найбільшу кількість букв ш, щ;
г) номер останнього один по одному стовпця, у якому міститься найбільша кількість попарно різних символів.
422. При передруці тексту на друкарській машинці часто виходить так, що наприкінці рядка залишається кілька невикористаних позицій. Число невикористаних позицій міняється від рядка до рядка, і тому правий край видрукуваного тексту виходить нерівним. Типографський набір дає рівний правий край, зокрема, за рахунок збільшення проміжків між словами, що зустрічаються в рядку.
Пропонується задача вибору придатних проміжків. Дано символьну матрицю п  т, у кожнім з рядків котрої мається принаймні один пробіл, за яким випливає відмінний від пробілу символ (тобто мається принаймні одна група пробілів усередині рядка). За рахунок зміни груп пробілів усередині рядків треба домогтися того, щоб наприкінці кожної з рядків пробіли були відсутні. Кількості пробілів у різних групах, що розташовуються усередині однієї і того ж рядка, повинні розрізнятися не більше ніж на одиницю.
т, у кожнім з рядків котрої мається принаймні один пробіл, за яким випливає відмінний від пробілу символ (тобто мається принаймні одна група пробілів усередині рядка). За рахунок зміни груп пробілів усередині рядків треба домогтися того, щоб наприкінці кожної з рядків пробіли були відсутні. Кількості пробілів у різних групах, що розташовуються усередині однієї і того ж рядка, повинні розрізнятися не більше ніж на одиницю.
423. Виконання наступних завдань не вимагає залучення вкладених циклів при роботі з матрицями. Подібні не занадто часті ситуації виникають, як правило, тоді, коли чи обробляються досліджуються
Додамо, що введення і висновок матриці в деяких Мовах програмування природно задавати за допомогою вкладених (подвійних) циклів.
елементи, що утворять «одномірну» частина матриці: рядок, стовпець, діагональ і т.д.
Дано дійсну квадратну матрицю порядку п.
а) Знайти суму елементів першого стовпця.
б) Знайти суму елементів головної і побічної діагоналей.
в) Знайти найбільше зі значень елементів першого й останнього рядків.
г) Знайти найменше зі значень елементів побічної діагоналі і двох сусідніх з нею ліній.
д) Для даного натурального т (т < 2п) знайти суму тих елементів матриці, сума індексів яких дорівнює т.
е) З'ясувати, чи вірно, що найбільше зі значень елементів головної діагоналі більше, ніж найменше зі значень елементів побічної діагоналі.
§ 12. Використання процедур
424. Дано дійсні числа s, t. Одержати
f(t - 2s, 1.17) + f (2.2, t, s-t),
де.
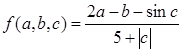
.425. Дано дійсні числа s, t. Одержати
g(l.2, s) + g(t, s)—g(2s—1, st).
де
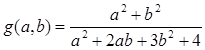
426.; Дане дійсне число y. Одержати
 , де
, де 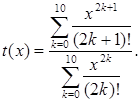
427.Дані дійсні числа а, b, с. Одержати
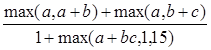
428. Дано дійсні числа а, b. Одержати
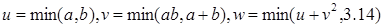
429. Дано натуральні числа п, т, цілі числа 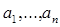
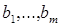 a
a 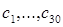 . Одержати
. Одержати
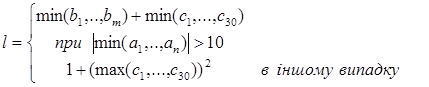
430. Дано натуральні числа k, I, т, дійсні числа 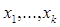
 a
a  . Одержати
. Одержати
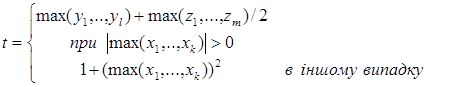
431 Дані дійсні числа s,t. Одержати 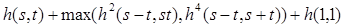
де 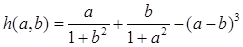
432. Дано дійсні, числа 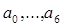 . Одержати для х =1, 3, 4 значення р (х + 1) – р (х), де
. Одержати для х =1, 3, 4 значення р (х + 1) – р (х), де 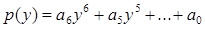
433. Дано дійсні числа s, t, 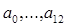 Одержати p(l)—p(f) + p2 (s — f)—p3 (1), де
Одержати p(l)—p(f) + p2 (s — f)—p3 (1), де

434. Дано дійсні числа 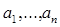
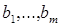 . У послідовності
. У послідовності 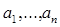 в послідовності
в послідовності 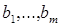 усі члени, що випливають за членом з найбільшим значенням (за першим один по одному, якщо їх трохи), замінити на 0.5.
усі члени, що випливають за членом з найбільшим значенням (за першим один по одному, якщо їх трохи), замінити на 0.5.
435. Дано цілі числа 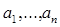
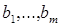
Якщо в послідовності 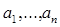 немає жодного члена зі значенням k, те перший один по одному член цієї послідовності, не менший всіх інших членів, замінити на значення k. По такому ж правилу перетворити послідовність,
немає жодного члена зі значенням k, те перший один по одному член цієї послідовності, не менший всіх інших членів, замінити на значення k. По такому ж правилу перетворити послідовність, 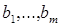 стосовно до значення 10.
стосовно до значення 10.
436. Дано цілі числа 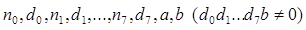 . Обчислити за схемою Горнера
. Обчислити за схемою Горнера 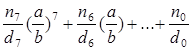 - визначивши процедури повного скорочення раціонального числа, заданого чисельником і знаменником, а також процедури додавання і множення раціональних чисел.
- визначивши процедури повного скорочення раціонального числа, заданого чисельником і знаменником, а також процедури додавання і множення раціональних чисел.
437. Дано цілі числа 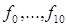 . Досліджувати існування цілочиселених коренів рівняння
. Досліджувати існування цілочиселених коренів рівняння 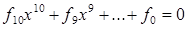 (Якщо fa=0, то мається корінь 0; якщо ж fg ^= 0, те целочисленный корінь, якщо він існує, належить кінцевій безлічі позитивних і негативних дільників числа fy.) Тут корисно визначить процедуру обчислення за схемою Горнера значення багато члена, а також процедуру, що по двох заданих числах k і т (т > k > 0) дозволяє визначити значення найменшого дільника числа т, що міститься серед чисел k+ 1, k+2,..., т.
(Якщо fa=0, то мається корінь 0; якщо ж fg ^= 0, те целочисленный корінь, якщо він існує, належить кінцевій безлічі позитивних і негативних дільників числа fy.) Тут корисно визначить процедуру обчислення за схемою Горнера значення багато члена, а також процедуру, що по двох заданих числах k і т (т > k > 0) дозволяє визначити значення найменшого дільника числа т, що міститься серед чисел k+ 1, k+2,..., т.
438. Дано натуральне число п, дійсні числа 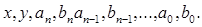 Обчислити за схемою Горнера значення багаточлена з комплексними коефіцієнтами
Обчислити за схемою Горнера значення багаточлена з комплексними коефіцієнтами
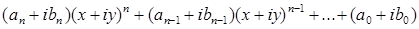
(Визначити процедури виконання арифметичних операцій над комплексними числами.)
439. Дано дійсні числа 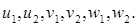 Одержати
Одержати  , де u, v, w-комплексні числа
, де u, v, w-комплексні числа 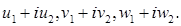 (Визначити процедури виконання арифметичних операцій над комплексними числами.)
(Визначити процедури виконання арифметичних операцій над комплексними числами.)
440. Дано натуральне число п, цілі числа 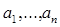 ,. Розглянути відрізки послідовності
,. Розглянути відрізки послідовності 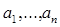 Отрута (підпослідовності членів, що підряд йдуть), що складаються з
Отрута (підпослідовності членів, що підряд йдуть), що складаються з
а) повних квадратів;
б) ступенів п'ятірки;
в) простих чисел.
У кожнім випадку одержати найбільшу з довжин що розглядаються відрізків. (Визначити процедури, що дозволяють розпізнавати повні квадрати, ступені п'ятірки, прості числа.)
441. Дано натуральне число п. Серед чисел 1,2,......, п знайти всі ті, котрі можна представити у виді суми квадратів двох натуральних чисел. (Визначити процедуру, що дозволяє розпізнавати повні квадрати.)
442. Дано дійсні числа  Знайти периметр десятикутника, вершини якого мають відповідно координати
Знайти периметр десятикутника, вершини якого мають відповідно координати 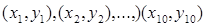 - (Визначити процедуру обчислення відстані між двома крапками, заданими своїми координатами.)
- (Визначити процедуру обчислення відстані між двома крапками, заданими своїми координатами.)
Дата добавления: 2015-10-13; просмотров: 269 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вкладені цикли | | | Обчислення із зберіганням порслідовностей, число члені якої залежить ві початкових даних. |