Методика расчета валов

При расчете валов на изгиб и кручение по гипотезам прочности мы будем учитывать только крутящий и изгибающие моменты, действующие в опасном поперечном сечении, и не будем принимать во внимание поперечные силы, так как соответствующие им касательные напряжения относительно невелики.

Максимальные нормальные (s) и касательные (t) напряжения у круглых валов вычисляют по формулам:

причем для круглых валов выполняется условие: 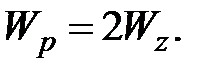(2)

При сочетании изгиба и кручения опасными будут точки поперечного сечения вала, наиболее удаленные от нейтральной оси.

Применив III гипотезу прочности, получим

. (3)

Выражение, стоящее в числителе, назовем эквивалентным моментом

,

тогда расчетная формула для круглых валов принимает вид

.

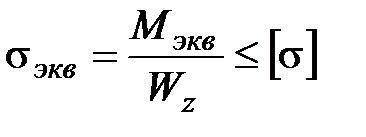По этой формуле расчет валов ведут, как на изгиб, но не по изгибающему, а по эквивалентному моменту.

Применив V гипотезу прочности, получим

, (6)

тогда по энергетической теории прочности

.

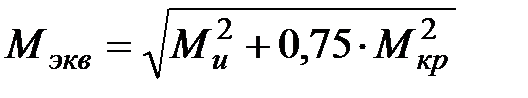Выполненный проектный расчет вала по гипотезам прочности проверяется расчетом на прочность при напряжениях, переменных во времени - динамических нагрузках.

В проектном расчете не учитывалось то, что напряжения в сечениях вала изменяются во времени по циклическому закону, поперечные сечения вала имеют очаги концентрации напряжений (шпоночные канавки), а так же не учитывался масштабный фактор, качество поверхности и пр.

Проверочный расчет выполняется для определения коэффициента запаса прочности с учетом всех факторов риска и сравнения найденного значения с принятым нормативным значением.

Условие прочности имеет вид

,

где [ п ] – нормальный коэффициент запаса прочности;

п – фактический коэффициент запаса прочности данной детали при данном цикле напряжений.

При сложном напряженном состоянии общий коэффициент запаса прочности определяют по эмпирической формуле:

где n _σ - коэффициент запаса прочности по нормальным напряжениям определяется по формулам:

при симметричном цикле напряжений ;

при асимметричном цикле напряжений . (11)

В приведенных формулах коэффициента запаса прочности:

– предел выносливости стандартного лабораторного образца при изгибе или растяжении-сжатии при симметричном цикле напряжений;

– эффективный коэффициент концентрации напряжений;

–масштабный фактор;

β – коэффициент качества поверхности;

– среднее напряжение цикла;

– амплитуда цикла напряжения;

– максимальное нормальное напряжение цикла;

– минимальное нормальное напряжение цикла;

– максимальный изгибающий момент;

– минимальный изгибающий момент;

W_z = 0,1 d ³ – осевой момент сопротивления вала;

d – диаметр поперечного сечения вала;

Ψ_σ – коэффициент, учитывающий влияние асимметрии цикла на предел выносливости, который при < 0 принимает нулевое значение (Ψ_σ = 0).

Напряжения ; ; 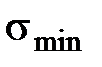могут быть положительными, отрицательными и равными нулю. Амплитуда всегда положительна.

Безразмерная величина называется коэффициентом асимметрии цикла.

Дата добавления: 2015-09-07