Потенциальная энергия деформации

Из закона сохранения энергии потенциальная энергия деформации равна работе продольных сил на перемещение :

.

Используя формулу (5), получаем

3.Общие теоремы динамики точки. Для решения многих задач динамики вместо метода интегрирования дифференциальных уравнений движения оказывается более удобным пользоваться общими теоремами, являющимися следствиями основного закона динамики./ Теорема об изменении количества движения: изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих сил за тот же промежуток времени 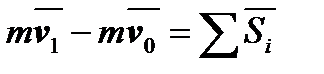. Эти выражения удобнее записывать в проекциях на оси. Теорема об изменении момента количества движения: . Теорема об изменении кинетической энергии: изменения кинетической энергии точки при некотором его перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении 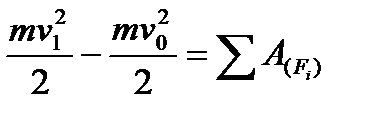./ Силы зависящие только от координат точки называются потенциальными силами (сила тяжести). Скалярная величина, равная работе, которую совершат потенциальные силы при перемещении точки из данного положения в нулевое называется потенциальной энергией (П). Закон сохранения механической энергии: при движении под действием потенциальных сил сумма кинетической и потенциальной энергий системы в каждом ее положении остается постоянной

4.Общие теоремы динамики системы. Теорема о движении центра масс: Механической системой называется совокупность материальных точек или тел, в которой положение или движение каждой точки (или тела) зависит от положения или движения всех остальных составляющих. Масса системы М равна сумме масс материальной точки. Характеристикой распределения масс в системе является центр масс, за которую принимается точка «С», положение которой определяется радиусом – вектором . В проекциях на оси , , . В ряде случаев для определения характера движения системы (например, твердого тела) достаточно знать закон движения ее центра масс . Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Проектируя на оси координат получаем дифференциальные уравнения движения центра масс: , , . Теорема об изменении количества движения системы: Количеством движения системы называют векторную величину Q, равную геометрической сумме (главному вектору) количеств движения всех точек системы . Можно показать, что количество движения системы равно произведению массы системы на скорость ее центра масс: . Теорема об изменении количества движения системы в интегральной форме: . В дифференциальной форме эта теорема имеет вид . Теорема об изменении главного момента количества движения . Теорема об изменении кинетической энергии системы: Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил .

4.Основные понятия и законы динамики. Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил. Здесь предполагается, что силы могут изменяться во времени./ Свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил называется инертностью. Величина зависящая от количества вещества и определяющая меру инертности называется массой. Тело, размерами которого при изучении его движения можно пренебречь называется материальной точкой. Тело можно считать материальной точкой, когда расстояния проходимые телом при движении, велики по сравнению с его размерами (снаряд). Поступательно движущееся тело тоже материальная точка. Твердое тело или механизмы всегда можно разбить на систему материальной точки (звенья). Поэтому раздел динамики обычно разделяют на динамику точки и динамику системы материальной точки. При вращательном движении мерой инертности служит момент инерции относительно оси вращения, который равен произведению массы на квадрат расстояния до этой оси . Часто момент инерции тела определяют выражением , где r_u – радиус инерции. Для простейших однородных тел существуют формулы для вычисления моментов инерции относительно центральных осей. Момент инерции тела относительно оси z, параллельной центральной оси z₀, и отстоящей от нее на расстоянии d, вычисляется по теореме Гюйгенса-Штейнера ./ Динамика базируется на основных законах механики: І закон (Галилея, закон инерции): изолированная от внешних воздействий материальная точка сохраняет состояние покоя или равномерного движения до тех пор, пока не будут приложены к ней внешние силы. II закон Ньютона – основной закон динамики: . ІІІ закон Ньютона: сила действия равна силе противодействия.

5.Определение внутренних сил методом сечений. Понятие напряжения.Сопротивление тел, оказываемое внешними воздействиями, обуславливается наличием в них внутренних сил, природа которых объясняется молекулярным строением материи. Внутренние силы – это результат взаимодействия частиц одного и того же тела. Величина внутренних сил зависит от величины действующих на тело внешних сил, и характеризует прочность тела, и является объектом нашего изучения./ Внутренние силы определятся методом сечений. Суть метода сечений. Алгоритм действий: разрезаем, отбрасываем, заменяем, составляем уравнение равновесия, определяем из них внутренние силы. Существует, в общем случае, 6 внутренних силовых факторов: - продольная сила (растяженние-сжатие); , - поперечные силы (сдвиг); - крутящий момент (кручение); , 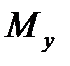- изгибающий момент

(изгиб)./ Соответственно этим силам различают следующие простейшие виды деформации: растяжение-сжатие, сдвиг, кручение, изгиб.

Дата добавления: 2015-09-07