Расчёт верхней части колонны.

Таблица 10

Нагрузки в надкрановой части колонны.

Сочетания	+Mmax, Ns	- Mmax, Ns	Nmax, |Ms|
Сечение	M	N	M	N	M	N
B	114,61	-296,9	-873,6	-395,3	42,2	-395,3
Cv	853,28	-454	-318,9	-552,5	746,1	-552,5

M=853,28 кН·м, N=454 кН

Рис. 23 Расчётное сечение колонны.

i_x≈0,43h_v=0,43·1=0,43 м=43см

ρ_x≈0,35h_v=0,35·1=35см

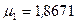[табл]

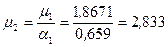
[прил. 10]=> η=(1,9-0,1m)-0,02(6-m) =(1,9-0,1·4,37)-0,02(6-4,37) ·1,43=1,416

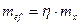=1,416·4,37=6,188

По прил. 8 φ_e=0,20371

Требуемая площадь сечения:

см²

Компоновка сечения:

Задаюсь толщиной полки t_f=12 мм,

Высота стенки h_w=h_v-2·t_f=100-2·1,2=97,6 см

Из условия устойчивости стенки определяю её толщину:

Т.к. , то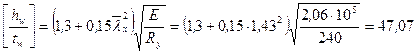

[t_w]=97,6/47,07=2,07см

Ограничивая рабочую часть стенки принимаю t_w=10мм (устойчивость стенки не обеспечивается, поэтому за рабочее сечение стенки принимаем 2сt_w)

- > c=24см

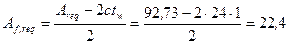см²

Принимаю t_f=1,2см,

м

Из условия устойчивости верхней части колонны из плоскости действия момента ширина полки

Принимаю

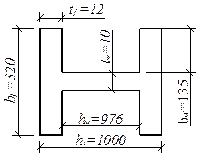
Рис. 24. Сечение колонны.

Геометрические характеристики сечения.

A=2·32·1,2+1·97,6=174,4 см²

A₀=2A_f+2ct_w=2·32·1,2+2·24·1=124,8 см²

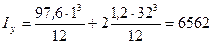см⁴

см⁴

см³

Проверка устойчивости верхней части колонны в плоскости действия момента.

Проверку устойчивости сплошной внецентренно сжатой колонны выполняем по формуле , где φ_е – коэффициент снижения расчетного сопротивления при внецентренном сжатии зависит от условной гибкости стержня и приведенного эксцентриситета.

При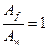

При 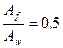η=1,25

Для η=1,318

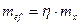=1,318·6,19=8,15

По прил. 8 φ_e=0,1606

Условие местной устойчивости полки:

Проверка устойчивости верхней части колонны из плоскости действия момента.

Проверку устойчивости из плоскости действия момента выполняем по следующей формуле

Рис. 25. Определение расчётного сечения.

Расчётный момент принимается М ≥ 0,5M_max=853,28 кН·м

Принимаю М=426,64, N=407,63 кН

φ_y=0,629

При m_x=5: c=β/(1+α·m_x)=1/(1+0,959·6,19)=0,144

При m_x=10: c=1/(1+ m_xφ_y)=1/(1+6,19·0,629)=0,204

По прил. 11.

С=С₅(2-0,2m_x)+C₁₀(0,2m_x-1)=0,144(2-0,2·6,19)+0,204(0,2·6,19-1)=0,158

Т.к. α>1 то

Т.к. то в расчетное сечение включаем полное сечение стенки

Дата добавления: 2015-09-06