Электромеханические характеристики асинхронных двигателей

Для вывода уравнения механической характеристики воспользуемся упрощенной схемой замещения двигателя (см. рис. 3.3), где обозначено: 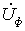– фазное напряжение; – фазный ток статора и приведенный фазный ток ротора соответственно; – ток намагничивания, приблизительно равный току холостого хода двигателя; x ₁, x ₂ ' – индуктивное сопротивление рассеяния обмотки статора и приведенное индуктивное сопротивление обмотки ротора; R ₁, R ₂ ' – активное сопротивление обмотки статора и приведенное сопротивление обмотки ротора; R _μ, x _μ – активное и реактивное сопротивление контура намагничивания, которые определяются параметрами взаимоиндукции статорной и роторной цепей. Такую схему замещения можно построить на основании уравнений (3.6), если принять

C ₁≈1+ x ₁/ x _μ≈1,

где C ₁ – модуль комплексного коэффициента, характеризующего соотношение сопротивлений статорной цепи и цепи контура намагничивания.

Рис. 3.3. Схема замещения асинхронного двигателя

В соответствии со схемой замещения можно получить выражение для тока ротора:

(3.7)

Электромагнитная мощность, передаваемая через воздушный зазор, определяется выражением

P _э= M ω₀,

где M – момент на валу двигателя. Механическая мощность на валу двигателя определяется выражением

P = M ω.

Потери мощности в цепи ротора представим в виде

(3.8)

Δ P = P _э− P = M (ω₀−ω)= M · s ω₀.

С другой стороны, потери мощности в цепи трехфазного ротора определяются выражением

(3.9)

Δ P =3(I ₂ ')² R ₂ '.

Приравнивая правые части уравнений (3.2) и (3.3), выразим момент двигателя через ток ротора:

M =3(I ₂ ')² R ₂ ' /(ω₀ s).

Подставляя в последнее выражение I ₂ ' из (3.7), получим

(3.10)

M (s)=3 U _ф² R ₂ ' /[ω₀ s ((R ₁+ R ₂ ' / s)²+(x ₁+ x ₂ ')²)].

Выражение (3.10) является механической характеристикой асинхронного двигателя. Нетрудно заметить, что при s →0 и при s →∞ момент M →0, следовательно, функция момента имеет максимум. Известным способом, из уравнения ∂ M /∂ s =0 определим значение критического скольжения s _к, при котором двигатель развивает максимальный (критический) момент:

(3.11)

где

x _к= x ₁+ x ₂ '.

Подставляя полученное значение s _к в (3.10), получим выражение для критического момента

(3.12)

Здесь знак «+» соответствует двигательному режиму, а знак «–» – генераторному.

Если выражение (3.10) разделить на (3.12), то после преобразований получим уравнение приведенной механической характеристики

(3.13)

M (s)=2 M _к(1+ as _к)/(s / s _к+ s _к/ s +2 as _к).

где a = R ₁/ R ₂ '.

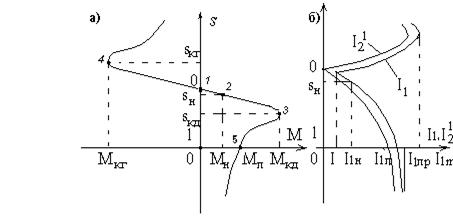
Рис. 3.4. Механическая и электромеханическая характеристики асинхронного двигателя

Механическая характеристика, соответствующая (3.13), представлена на рис. 3.4.а. Она имеет несколько характерных точек:

1. s =0, M =0 – точка холостого хода, скорость равна синхронной;

2. s = s _н, M = M _н – точка номинального режима, скорость равна номинальной;

3. s = s _кд, M = M _кд – точка максимального момента в двигательном режиме;

4. s =− s _кг, M = M _кг – точка максимального момента в генераторном режиме;

5. s =1, M = M _п – точка пускового режима.

Существуют асинхронные двигатели, у которых механическая характеристика дважды меняет знак жесткости. Тогда выделяют точки минимального момента для двигательного и генераторного режимов.

Значение пускового момента просто получить из (3.13), принимая s =1:

(3.14)

M _п=2 M _к s _к(1+ as _к)/(1+ s _к²(1+2 a)).

В ряде случаев, пренебрегая активным сопротивлением обмотки статора, при s < s _к выражение момента можно представить линеаризованной зависимостью

(3.15)

M (s)= s / s _к·2 M _к.

На рабочем участке характеристики это выражение оказывается достаточно точным. Из (3.15) получим простое приближенное соотношение для определения жесткости на рабочем участке характеристики

(3.16)

β=2 M _к/ s _к,

Уравнение (3.7) можно назвать электромеханической характеристикой двигателя, но только по отношению к вторичному приведенному току. Как следует из схемы замещения, ток, потребляемый двигателем, равен векторной сумме приведенного к статору тока ротора (I ₂ ') и тока намагничивания (I _μ). Последний, в первом приближении, можно считать постоянным. Тогда с учетом (3.7) электромеханическая характеристика двигателя имеет вид рис. 3.4.б, где обозначено I _μ – ток намагничивания, I _1н – номинальный потребляемый ток двигателя, I _1п – пусковой ток, I _1пр – предельный ток двигателя, который он имеет при s =±∞, I _1м – максимальный ток двигателя.

Искусственные характеристики асинхронного двигателя получим из уравнений (3.11) и (3.12), согласно которым s _к и M _к изменяются при изменении следующих параметров: фазного напряжения, активного сопротивления цепи ротора, индуктивного и активного сопротивления цепи статора, и, в неявном виде, при изменении частоты питания двигателя. Соответствующее этим изменениям семейство искусственных характеристик в первом квадранте плоскости s – M представлено на рис. 3.5.

Можно отметить, что согласно (3.11) и (3.12) при изменении активного сопротивления в цепи ротора момент критический не изменяется, а скольжение увеличивается при увеличении сопротивления – рис. 3.5.а, т.е. при введении добавочного сопротивления в цепь ротора жесткость механической характеристики уменьшается.

При изменении фазного напряжения неизменным остается критическое скольжение, критический момент уменьшается при уменьшении напряжения, т.е. жесткость механической характеристики также уменьшается, рис. 3.5.б.

При увеличении индуктивного сопротивления обмотки статора, например, путем введения в его цепь реактора (дросселя) примерно пропорционально уменьшаются и скольжение и критический момент, поэтому жесткость уменьшается, рис. 3.5.в.

При изменении частоты напряжения питания двигателя, во-первых, пропорционально изменяется скорость вращения поля статора, во-вторых, одновременно меняются и скольжение, и критический момент, рис. 3.3.г. Более подробно характеристики двигателя при изменении частоты мы рассмотрим ниже.

Дата добавления: 2015-09-05