Метод аналитической аппроксимации

Метод основан на аппроксимации характеристики нелинейного элемента аналитической функцией, которая должна, с одной стороны, достаточно точно отображать исходную нелинейную характеристику на участке перемещения рабочей точки, а с другой стороны, обеспечивать возможность достаточно несложного интегрирования полученного дифференциального уравнения (в частности, с использованием табличных интегралов).

Метод применим к нелинейным цепям с одним накопителем энергии, описываемым дифференциальными уравнениями первого порядка, а также к цепям, описываемым уравнениями, сводящимися к уравнениям первого порядка путем замены переменных.

Ценность метода заключается в получении выражения исследуемой величины в общем виде, что позволяет осуществлять требуемый анализ процессов при варьировании параметров схемы.

10. Переходные процессы при М, Мс =const и при Мс=const, М линейно зависящей от скорости.

а) M = const, M_с = const

Начнем рассмотрение задач первой группы с простейшего случая, когда в переходном процессе M = const, и M_с = const.

а) б)

Рис. 2. Механические характеристики (а) и временные зависимости (б) при М = const и M_c = const

Пусть привод (рис. 1) работал в точке w _нач, М _нач = М _с (рис. 2) некоторой характеристики (она нас не интересует) и в момент времени t = 0 был мгновенном переведен на новую характеристику, показанную на рис. 2,а жирной линией.

Уравнение (1) в этом случае - дифференциальное уравнение с разделяющимися переменными и его решение имеет вид:

Постоянную интегрирования С найдем из начального условия - при t = 0, w = w _нач:

w _нач = С.

Окончательно будем иметь:

(2)

Это решение действует на интервале w _нач < w < w _кон, так как по условию при w = w _кон функция w (М) терпит излом. На этом интервале М =М₁.

Графики переходного процесса приведены на рис. 2,б. Время переходного процесса t _пп можно найти, подставив в (2) w = w _кон и решив относительно t:

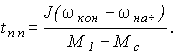(3)

Этот же результат, конечно, можно получить, решив (1) относительно dt и взяв определенный интеграл:

Рассмотренный простейший случай имеет очень большое практическое значение, так как к нему может быть сведено в целях оценки времени и характера переходного процесса большое число конкретных задач.

Пример. Оценить время пуска t_п и построить приближенный график переходного процесса пуска короткозамкнутого асинхронного двигателя с известными механической характеристикой, М_с и J (рис. 3,а). Заменим реальную характеристику (сплошная линия) приближенной (пунктирная линия) и применив (3), получим:

а) б)

Рис. 3. Механические характеристики (а) и графики переходных процессов

w (t) и M(t) при пуске асинхронного двигателя

.

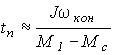Зная t_п, можно построить приближенные графики переходного процесса (пунктир на рис. 3,б). Эти графики будут отличаться от действительных (сплошные линии на рис. 3,б), однако во многих случаях полученная оценка может быть весьма полезной.

б) М_с = const, M линейно зависит от w, b < 0.

Пусть характеристики двигателя и механизма имеют вид, представленный на рис. 4. Уравнение линейной механической характеристики двигателя с отрицательной жесткостью может быть записано как

Рис. 4. Механические характеристики и графики переходных процессов w (t) и M(t) при линейной зависимости w (М)

(4)

или

(5)

где - жесткость механической характеристики; для линейной характеристики .

Подставив (5) в (1), после простых преобразований получим:

Выражение в правой части, как следует из (4), представляет собою w _кон. Обозначив коэффициент перед производной через Т _м, запишем:

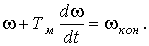(6)

Теперь подставим в (1) вместо ее выражение, полученное из (4):

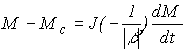
или, используя принятые выше обозначения,

(7)

Итак, мы обнаружили, что в рассматриваемом переходном процессе как для скорости, так и для момента справедливо одинаковое уравнение вида

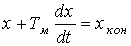, (8)

то есть линейное неоднородное дифференциальное уравнение с постоянной правой частью.

Коэффициент при производной

(9)

называют электромеханической постоянной времени.

Рис. 5. К определению электромеханической постоянной времени Т_м

Для выяснения смысла этой величины рассмотрим условный привод с характеристикой, показанной на рис. 5. Определив время разгона такого привода по (3)

замечаем, что оно выражается так же, как Т _м. В связи с этим можно считать, что электромеханическая постоянная времени Т _м представляет собою время, за которое привод разогнался бы вхолостую до w = w ₀ под действием момента короткого замыкания. Другие выражения для Т _м приведены в (9). В некоторых частных случаях оказывается удобным выражать Т _м через параметры привода. Так, для двигателя постоянного тока независимого возбуждения можно выразить жесткость характеристики как (см. п. 3.2)

Подставив это выражение в (9), получим

(9,а)

Правая часть уравнения (8) представляет собою конечное значений переменной, то есть установившуюся величину, которая будет достигнута после окончания переходного процесса.

Решение (8), как известно, имеет вид

x = x_cв + х_пр = Ае^pt + х_кон,

где p - корень характеристического уравнения

1 + pТ_м = 0,

то есть

А - постоянная, определяемая из начального условия:

t = 0, x = x_нач,

то есть

А = х_нач - х_кон.

Итак, окончательно имеем:

(10)

то есть скорость и момент изменяются в переходном процессе от начальных до конечных значений по экспоненциальному закону с постоянной времени Т_м (см. рис. 4).

Напомним некоторые важные свойства экспоненты.

1. Касательная в любой точке отсекает на линии установившегося состояния отрезок, равный Т_м.

2. За время t = Т_м изменение величины составляет 0,632 от полного изменения.

3. За время t = 3 Т_м изменение составляет 0,95 от полного. В дальнейшем мы будем считать, что процесс устанавливается за t = 3 Т_м.

11. Общие сведения о регулировании координат. Отличие регулирования координат от изменения. Основные показатели регулирования координат: направление регулирования, плавность, стабильность поддержания скорости, диапазон регулирования, быстродействие, перегулирование и т.д.*

Как отмечалось выше, основная функция электропривода состоит в управлении его координатами - скоростью и моментом, т.е. в их принудительном направленном изменении в соответствии с требованиями технологического обслуживаемого процесса.

Очень важный частный случай управления координатами - регулирование скорости или момента, т.е. принудительное изменение этих величин в установившемся режиме в соответствии с требованиями технологического процесса посредством воздействия на механическую характеристику двигателя. Частным случаем регулирования является поддержание одной из координат на требуемом уровне при независимом изменении другой координаты.

Чаще всего регулируемой координатой служит скорость: необходимо изменять скорость транспортного средства в зависимости от условий движения, состояния дороги и т.п., нужно регулировать скорость насоса, чтобы обеспечивать нужный напор в системе водоснабжения, требуется поддерживать на заданном уровне скорость движения жилы кабеля в процессе наложения на нее изоляции и т.п.

12. Схема включения двигателя постоянного тока независимого возбуждения. Законы, описывающие принцип работы привода постоянного тока.

Для получения простейшей модели электропривода постоянного тока, описывающей установившиеся (статические) режимы и позволяющей получить основные характеристики, воспользуемся схемой на рис. 3.1.

Будем полагать, что якорная цепь питается от независимого источника с напряжением U ^*, сопротивление цепи якоря R постоянно, магнитный поток Ф определяется лишь током возбуждения и не зависит от нагрузки (реакция якоря не проявляется), индуктивные параметры цепей пока не учитываются, поскольку рассматриваются лишь установившиеся (статические) режимы.

Рис. 3.1. Схема электропривода с двигателем постоянного тока

Взаимодействие тока I в обмотке якоря с магнитным потоком Ф, создаваемым обмотками, расположенными на полюсах машины, приводит в соответствии с законом Ампера и возникновению электромагнитных сил, действующих на активные проводники обмотки и, следовательно, электромагнитного момента М:

М = kФI (3.1)

где k - конструктивный параметр машины.

В движущихся с угловой скоростью в магнитном поле под действием момента М проводниках обмотки якоря в соответствии с законом Фарадея наводится ЭДС вращения Е:

E = kФw, (3.2)

направленная в рассматриваемом случае встречно по отношению к вызвавшей движение причине - ЭДС источника питания U.

В соответствие со вторым законом Кирхгоффа для якорной цепи машины справедливо уравнение:

U-E = IR. (3.3)

Уравнения (3.1)-(3.3) - простейшая, но достаточная для понимания главных процессов в электроприводе постоянного тока модель. Для решения практических задач они должны быть дополнены уравнением движения с моментом потерь 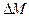, входящим в М_с,

и уравнениями цепи возбуждения для конкретной схемы электропривода.

Разумеется, в условиях каждой задачи должно быть строго оговорено, что задано и известно, а что нужно искать.

Рассмотрим подробнее роль, которую играет ЭДС Е в процессе преобразования энергии, осуществляемом электрической машиной. Если существовал некоторый установившийся режим М₁ = М_с1, а затем М_с изменился, например, возрос до величины М_с2, то для получения нового установившегося режима необходимо иметь средство, которое изменило бы М, приведя его в соответствие с новым значением М_с. В двигателе внутреннего сгорания эту роль выполнит оператор, увеличив подачу топлива; в паровой турбине - специальный регулятор, который увеличит подачу пара. В электрической машине эту роль выполнит ЭДС. Действительно, при возрастании М_с скорость двигателя начнет снижаться, значит уменьшится в соответствии с (3.2) и ЭДС (полагаем для простоты, что Ф, а также U и R - постоянные). Из (3.3) следует, что

,

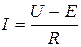следовательно, ток вырастет, обусловив тем самым рост момента в соответствии с (3.1). Двигатель автоматически, без каких-либо внешних воздействий перейдет в новое установившееся состояние. Эти процессы будут иметь место при любых величинах и знаках М_с, то есть ЭДС будет выполнять функцию регулятора как в двигательном, так и в тормозных режимах работы машины.

При использовании в электроприводе постоянного тока двигателя с независимым возбуждением - рис. 3.2 с питанием от источника напряжения U=const уравнение электромеханической характеристики w(I) получится подстановкой (3.2) в (3.3) и решением относительно :

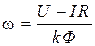(3.4)

Механическую характеристику w(М) получим, подставив в (3.4) ток, выраженный из (3.1):

. (3.5)

13. Структурная схема и передаточные функции электропривода постоянного тока без учета упругости.

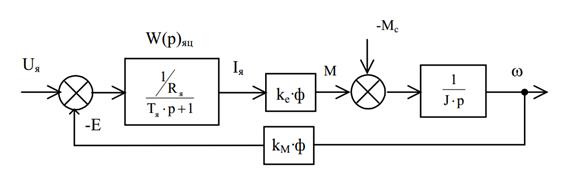
14. Тормозные режимы работы электропривода с двигателем постоянного тока с независимым возбуждением.

Кроме двигательных режимов электродвигатели также могут работать в тормозных режимах. Тормозной режим характеризуется тем, что скорость вращения и момент двигателя имеют разные знаки. Быстрота и точность, с какой будут протекать переходные процессы остановки или реверса во многом определяют производительность механизма, а иногда и качество вырабатываемого продукта. Возможны три варианта электрического торможения:

1) рекуперативное торможение;

2) динамическое торможение;

3) торможение противовключением.

Каждый тормозной режим является генераторным, так как энергия поступает в машину с вала, преобразуется в электрическую и либо отдаётся в сеть, либо затрачивается на нагрев элементов якорной цепи, обладающих активным сопротивлением, и рассеивается в окружающую среду.

3.5.1. Рекуперативное торможение

Такой режим возникает, когда скорость двигателя больше скорость идеального холостого хода двигателя, то есть выполняется условие

.

При этом ЭДС двигателя становится больше напряжения сети (), и ток двигателя меняет направление. При этом двигатель работает генератором и отдает энергию в сеть. Электромагнитный момент двигателя при этом противодействует внешнему вращающему моменту.

Данный вид торможения является наиболее экономичным, так как энергия возвращается в сеть. Применение этого способа является эффективным энергосберегающим средством. Этот режим целесообразен, когда привод работает с частыми пусками и остановками. Например, электротранспорт. При движении под уклон также возникают благоприятные условия для возникновения этого режима торможения.

Схема включения двигателя для данного режима показана на рис. 3.6, а, а характеристики представлены на рис. 3.7 (характеристика 1).

3.5.2. Динамическое торможение

Необходимость в таком торможении возникает, когда после отключения двигателя от сети его якорь продолжает вращаться под действием запаса кинетической энергии. Если по технологии требуется более быстрый останов двигателя, чем время остановки на выбеге, используется динамическое торможение.

При данном способе торможения якорь двигателя замыкается на тормозное сопротивление, а обмотка возбуждения остаётся подключенной в сеть для создания тормозного момента. Вырабатываемая при этом энергия переходит в тепловую и рассеивается в окружающее пространство. В этом режиме ток двигателя меняет знак, так как он начинает протекать под действием ЭДС двигателя, которая направлена всегда встречно напряжению сети

.

Величину тормозного сопротивления можно определить из формулы

.

При этом слишком малое значение тормозного момента ведет к затягивания процесса торможения, а слишком большой ток отрицательно сказывается на работе щеточно-коллекторного аппарата двигателя.

Схема включения двигателя для данного режима показана на рис. 3.6, б, а характеристики на рис. 3.7 (характеристика 2).

а	б	в
Рис. 3.6. Схемы включения двигателя в тормозных режимах работы (а-рекуперативное, б-динамическое, в-противовключение)

Рис. 3.7. Механические характеристики ДПТ с НВ в тормозных режимах

3.5.3. Торможение противовключением

Для уменьшения времени торможения или реверса иногда применяют данный режим. Реализация этого режима возможна на работающем двигателе при смене полярности питающего напряжения. В этом случае направления ЭДС двигателя и напряжения сети совпадает

,

что без ограничения тока якоря приводит к большим величинам тока якоря, что является недопустимым.

Величина тормозного сопротивления выбирается по формуле

.

Торможение противовключением применяется в основном для реверса двигателя. Для точного останова двигателя данным режим не удобен, так как требуется довольно точная настройка аппаратуры для того, чтобы остановить двигатель в точке нулевой скорости. Если же двигатель не отключить от сети, то он перейдет в двигательный режим, и в дальнейшем разгонится до номинальной скорости при наличии номинального момента на валу двигателя. Для точной остановки двигателя используется режим динамического торможения.

Схема включения двигателя для данного режима показана на рис. 3.6, в, а характеристики на рис. 3.7 (характеристика 3).

15. Статические характеристики двигателя постоянного тока с последовательным возбуждением.

+-

---

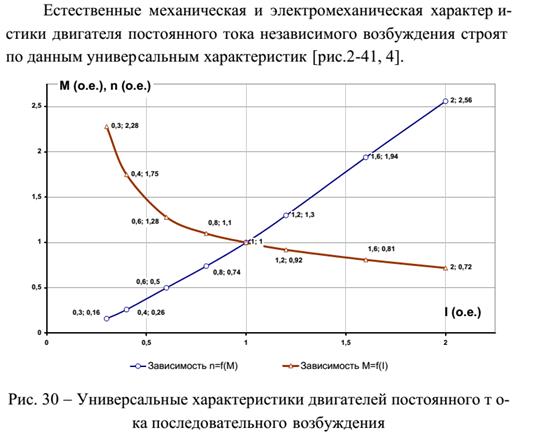
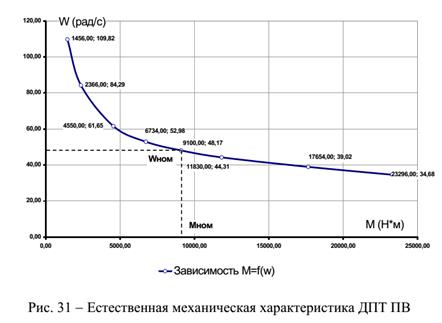
Дата добавления: 2015-09-05