Нахождение решений линейного однородного рекуррентного уравнения второго порядка. Нахождение чисел Фибаначи. Общее решение рекуррентного уравнения второго порядка

В случае, когда характеристическое уравнение имеет два различных вещественных корня и, каждая из последовательностей

и

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел и последовательность с общим членом

также удовлетворяет рекуррентной формуле.

Числа и называют произвольными постоянными.

В случае, когда характеристическое уравнение имеет два совпавших вещественных корня, непосредственная проверка показывает, что каждая из последовательностей

и

удовлетворяет рекуррентной формуле, поэтому для любых чисел и последовательность с общим членом

также удовлетворяет рекуррентной формуле.

В случае, когда характеристическое уравнение имеет два комплексных корня, каждая из последовательностей

и

удовлетворяет рекуррентной формуле, поэтому для любых чисел и последовательность с общим членом

также удовлетворяет рекуррентной формуле.

Здесь:

Re(x) – это вещественная часть комплексного числа, т.е. Есди x=a+b i, то Re(x)=a

Im(x) – мнимая часть комплексного числа, т.е. Есди x=a+b i, то Im(x)=bi

Пример

Для последовательности , удовлетворяющей линейному рекуррентному уравнению второго порядка 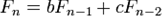с начальными значениями , , справедлива формула:

.

Для того, чтобы найти необходимо решить характеристическое уравнение . Если дискриминант этого уравнения отличен от нуля, то

где — любой из двух корней этого уравнения. Если же дискриминант характеристического уравнения равен нулю, то

В частности, для последовательности, определяемой следующим линейным рекуррентным уравнением второго порядка

; , .

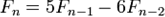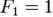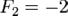корнями характеристического уравнения являются , . Поэтому

.

Окончательно:

Формула Бине выражает в явном виде значение F_n как функцию от n:

,

где — золотое сечение. При этом и являются корнями характеристического уравнения .

Из формулы Бине следует, что для всех , F_n есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .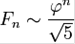

Формула Бине может быть аналитически продолжена следующим образом:

При этом соотношение F_{z + 2} = F_{z + 1} + F_z выполняется для любого комплексного числа z.

Дата добавления: 2015-09-06