Определение16.7.

Отношение эквивалентности (∼) на множестве X — это бинарное отношение, для которого выполнены следующие условия:

• Рефлексивность: для любого a в X,

• Симметричность: если , то ,

• Транзитивность: если и , то .

Запись вида «» читается как «a эквивалентно b».

• Классом эквивалентности C (a) элемента a называется подмножество элементов, эквивалентных a. Из вышеприведённого определения немедленно следует, что, если , то C (a) = C (b).

Множество всех классов эквивалентности обозначается X / ∼.

• Для класса эквивалентности элемента a используются следующие обозначения: [ a ], a / ∼, .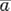

• Множество классов эквивалентности по отношению ∼ является разбиением множества.

• Равенство («»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.

• Сравнение по модулю, («а ≡ b (mod n)»).

• В Евклидовой геометрии

• Отношение конгруэнтности («»).

• Отношение подобия («»).

• Отношение параллельности прямых («»).

• Эквивалентность функций в математическом анализе:

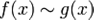Говорят, что функция эквивалентна функции при , если она допускает представление вида , где при . В этом случае пишут , напоминая при необходимости, что речь идет о сравнении функций при . Если при , эквивалентность функций и при , очевидно, равносильна соотношению .

• Отношение равномощности множеств.

Дата добавления: 2015-09-06