Стабилизаторы

Подмножество

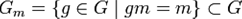
является 0%9F%D0%BE%D0%B4%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D0%B0"подгруппой группы G и называется стабилизатором или стационарной подгруппой элемента .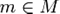

Стабилизаторы элементов одной орбиты сопряжены, то есть если n ∼ _Gm, то найдется такой элемент 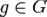, что

G_m = gG_ng ^{− 1}.

№48 Дать определение орбиты группы подстановок.

Орбиты

Подмножество

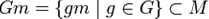
называется орбитой элемента .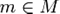

Действие группы G на множестве M определяет на нём 0%9E%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_%D1%8D%D0%BA%D0%B2%D0%B8%D0%B2%D0%B0%D0%BB%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B8"отношение эквивалентности

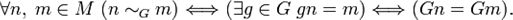
При этом 0%9A%D0%BB%D0%B0%D1%81%D1%81_%D1%8D%D0%BA%D0%B2%D0%B8%D0%B2%D0%B0%D0%BB%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B8"классами эквивалентности являются орбиты элементов. Поэтому, если общее число классов эквивалентности равно k, то

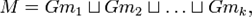
где попарно неэквивалентны. Для транзитивного действия k = 1.

№ 50 Лемм Бернсайда

Пусть G — конечная 0%93%D1%80%D1%83%D0%BF%D0%BF%D0%B0_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"группа, 0%94%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D0%B5_%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D1%8B"действующая на 0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE"множестве X. Для любого элемента g из G будем обозначать через X^g множество элементов X, оставляемых на месте g. Лемма Бёрнсайда даёт формулу числа 0%94%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D0%B5_%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D1%8B"орбит группы G, обозначаемого | X / G |:

Число орбит (0%9D%D0%B0%D1%82%D1%83%D1%80%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%B0"натуральное число или бесконечность) равно среднему количеству точек, оставляемых на месте элементом из G.

Дата добавления: 2015-09-06