Логическое тождество (эквиваленция)

Операцию логического тождества обозначают символами =, ↔, ~.

Интуитивно можно догадаться, что высказывания эквивалентны (равносильны), когда их значения истинности одинаковы.

Например, эквивалентны высказывания: "железо тяжёлое" и "пух лёгкий", так же как и высказывания: "железо лёгкое" и "пух тяжёлый". Обозначим эквиваленцию символом ↔ и запись "А ↔ В" будем читать "А эквивалентно В", или "А равносильно В", или "А, если и только если В".

Таким образом, эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны.

Высказывание типа "А, если и только если В" можно заменить высказыванием "Если А, то В и, если В, то А".

Следовательно, функцию эквиваленции можно заменить комбинацией функций импликации и конъюнкции.

Запишем таблицу истинности для эквиваленции (таблица 5):

Таблица 5 – Таблица истинности функции логического тождества (эквиваленция)

А	В	А ↔ В

Приведём примеры записи сложных высказываний с помощью обозначения логических связок:

"Быть иль не быть – вот в чём вопрос" (В. Шекспир) А V A ↔ В.

"Если хочешь быть красивым, поступи в гусары" (К. Прутков) А ↔ В.

2.6. Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Операция исключающее ИЛИ (неравнозначность, сложение по модулю два) обозначается символом и отличается от логического ИЛИ только при A=1 и B=1.

Таким образом, неравнозначность двух высказываний Х1 и Х2 называют
такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.

Определение данной операции может быть записано в виде таблицы
истинности (таблица 6):

Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Х1	Х2	Y

Как видно из таблицы 6, логика работы элемента соответствует его названию.

Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.

Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).

Таблица 7 – Основные логические операции

Обозначение операции	Читается	Название операции	Альтернативные обозначения
	НЕ	Отрицание (инверсия)	Черта сверху
^	И	Конъюнкция (логическое умножение)	&
v	ИЛИ	Дизъюнкция (логическое сложение)	+
→	Если … то	Импликация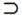
↔	Тогда и только тогда	Эквиваленция	~
XOR	Либо … либо	ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2)

3. Порядок выполнения логических операций
в сложном логическом выражении

Система логических операций инверсии, конъюнкции, дизъюнкции позволяет построить сколь угодно сложное логическое выражение.

При вычислении значения логического выражения принят определённый порядок выполнения логических операций.

1. Инверсия.

2. Конъюнкция.

3. Дизъюнкция.

4. Импликация.

5. Эквивалентность.

Для изменения указанного порядка выполнения операций используются
скобки.

Дата добавления: 2015-10-13