Прием и расходование малого груза

Предположим, что на судно принят относительно малый груз, сила тяжести которого p не превышает (5—10) % силы тяжести судна D. Обозначим через x_p, y_p, z_p координаты ЦТ принятого груза. В результате приема груза изменятся средняя осадка и остойчивость, могут возникнуть крен и дифферент судна. Для упрощения вывода расчетных формул разобьем рассматриваемую операцию на две части. Сначала примем груз таким образом, чтобы не возникало ни крена, ни дифферента. Эта часть операции будет сопровождаться изменением средней осадки и метацентрической высоты. Затем перенесем в горизонтальной плоскости груз в место его фактического приема. При этом могут появиться крен и дифферент.

Чтобы при приеме малого груза не возникало крена и дифферента, ЦТ груза должен располагаться на одной вертикали с ЦТ площади ватерлинии. Поэтому примем вначале груз в точку с координатами x_­f, 0, z_p, где аппликата z_p может быть любой. Изменение средней осадки определится формулой:. Найдем изменение поперечной метацентрической высоты, рассматривая его как сумму изменений слагаемых

. (10)

Изменение аппликаты ЦВ определяется формулой (см.модуль 4):

.

Изменение поперечного метацентрического радиуса равно, где — метацентрический радиус после приема груза; — метацентрический радиус до его приема. В формулах для r ₁ и r ₀ величина, а I_{x 1} и I_x — моменты инерции площади ватерлинии после и до приема груза соответственно. Поскольку принятый груз полагаем малым, борта судна в пределах изменения осадки можно считать вертикальными, т. е. площадь действующей ватерлинии неизменна и, следовательно,. Тогда

. (11)

Подставляя значения и в (10) с учетом выражения для h ₀ найдем

. (12)

Отсюда поперечная метацентрическая высота после приема груза равна

. (13)

Аналогичным путем определяется изменение продольной метацентрической высоты:

. (14)

Изменение продольного метацентрического радиуса находим аналогично,считая судно прямобортным

. (15)

После подстановки значений, и в (14) получим

. (16)

Для большинства судов величина много меньше H ₀. Поэтому приближенно можно положить

. (17)

Тогда продольная метацентрическая высота после приема груза равна

. (18)

В случае расходования груза величину p следует вводить со знаком минус.

Перейдем ко второй части операции: переместим груз в горизонтальной плоскости так, чтобы его ЦТ оказался в точке с координатами x_p и y_p.. Тогда изменения углов крена и дифферента будут равны

; (19)

. (20)

Проанализируем, как изменяются начальные метацентрические высоты при приеме (расходовании) малого груза в разные места по высоте судна. Рассматривая формулу (12), видим, что при аппликате ЦТ груза, равной

. (21)

изменение поперечной метацентрической высоты как в случае приема груза, так и в случае его расходования. Выражение (21) представляет собой уравнение горизонтальной плоскости, расположенной на высоте над основной. При приеме (расходовании) груза, ЦТ которого окажется на этой горизонтальной плоскости, поперечная метацентрическая высота не изменится. Такая горизонтальная плоскость называется нейтральной (иногда ее называют предельной). Если груз принят ниже нейтральной плоскости, т. е., то согласно формуле (12) — поперечная метацентрическая высота увеличится. Если же груз принят выше нейтральной плоскости, т. е., то — поперечная метацентрическая высота уменьшится. В случае расходования груза получается наоборот — снятие его с плоскости, лежащей ниже нейтральной плоскости, приводит к уменьшению поперечной метацентрической высоты, снятие же груза, расположенного выше нейтральной плоскости — к ее увеличению.

Рассматривая приближенную формулу (17), определяющую изменение продольной метацентри-ческой высоты, видим, что для большинства надводных судов прием любого малого груза приводит к уменьшению продольной метацентрической высоты, а любое расходование — к ее увеличению. Это объясняется расположением соответствующей нейтральной плоскости, которая согласно (16) приближенно описывается уравнением

, (22)

и, следовательно, практически всегда лежит ниже основной плоскости. Значит, груз, принятый или израсходованный в любом месте на судне, оказывается выше нейтральной плоскости, что должно приводить к уменьшению метацентрической высоты в случае приема и к ее увеличению в случае расходования груза.

1. 
   ^ Влияние на остойчивость подвешенного, перекатывающегося и жидкого грузов
1. 
   Подвешенный груз

Пусть груз p с ЦТ в точке B подвешен на судне или жестко связанном с ним устройстве в некоторой точке A (рис. 2, а). Если груз закреплен в этой точке, то при наклонении судна он перемещаться не сможет и дополнительного влияния на остойчивость не оказывает, этот груз просто войдет в нагрузку масс судна с координатами точки B как ЦТ. Если же груз не закреплен или в процессе наклонения судна освобождается, то ЦТ груза переместится в сторону наклонения, в точку B ₁. Линия подвеса, разумеется, останется вертикальной и перпендикулярной поверхности воды, а угол между линиями подвеса до наклонения и после него будет равен углу наклонения судна, например углу крена. Благодаря такому перемещению груза образуется пара сил и дополнительный кренящий момент

, (23)

где l — длина подвеса; — расстояние, на которое переместился груз в поперечной плоскости. При достаточно малых наклонениях судна

. (24)

Действие на судно дополнительного кренящего момента можно трактовать как уменьшение восстанавливающего момента. Поэтому восстанавливающий момент с учетом влияния подвешенного груза равен

. (25)

Величина pl / D — поправка к метацентрической высоте, обусловленная перемещением груза:

. (26)

Эта поправка всегда отрицательна; значит, влияние подвешенного груза можно рассматривать так же, как перемещение его ЦТ наверх, в точку подвеса, в результате чего аппликата ЦТ судна изменяется на

. (27)

Эта величина не зависит от угла наклонения, следовательно, она будет одной и той же при малых и больших углах крена, при наклонениях в поперечной и продольной плоскостя х. Таким образом, поправка к продольной метацентрической высоте равна

. (28)

При выводе всех этих формул на величину груза p никаких ограничений не накладывалось. Поэтому они справедливы как для малого, так и для большого подвешенного груза.

1. 
   ^ Перекатывающийся груз

Пусть на судне находится твердый груз, который при наклонении в некоторой плоскости перекатывается так, что его ЦТ перемещается в той же плоскости по кривой из точки B в точку B ₁ (рис. 2, б). Для каждого угла наклонения сила тяжести груза действует по нормали к кривой BB ₁ в соответствующей точке, вэта нормаль перпендикулярна плоскости действующей ватерлинии. Если точка B отвечает положению равновесия судна, а точка B ₁ — наклонению на малый угол, то линии действия силы тяжести груза для этих двух положений пересекутся в некоторой точке A. Но в этой же точке пересекутся соответствующие нормали к кривой BB ₁, поэтому в пределе при бесконечно малом угле наклонения точка A является центром кривизны кривой BB ₁ в точке B.

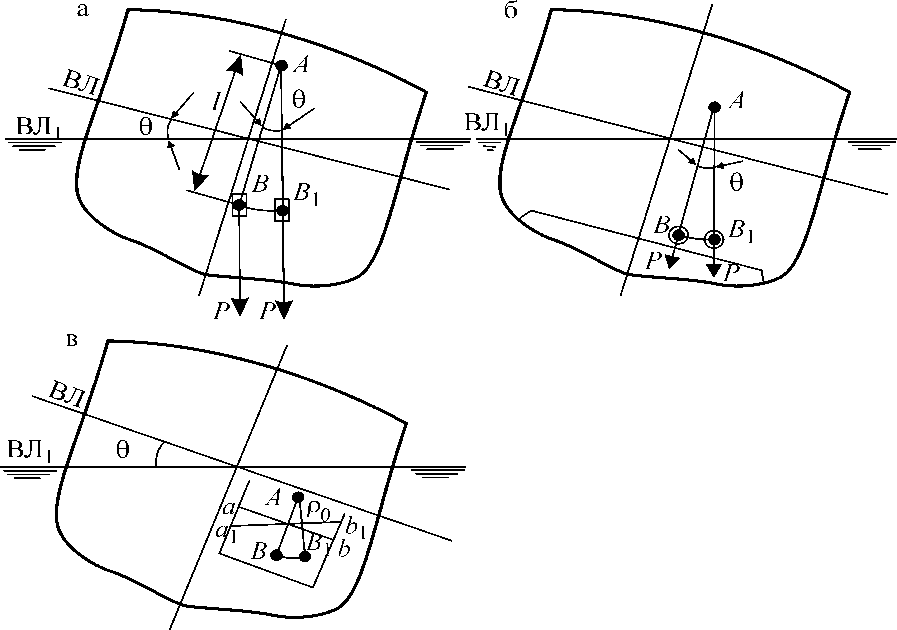
Рис.2. К оценке влияния на остойчивость: а — подвешенного; б — перекатывающегося; в — жидкого грузов

Сопоставляя рисунки (2, а) и (2, б), легко убедиться, что перекатывающийся груз оказывает точно такое же влияние на начальную остойчивость, как и груз, подвешенный в точке A. Положение этой точки определим радиусом кривизны l кривой, по которой перекатывается груз в данной плоскости наклонения. По аналогии с поправкой к метацентрической высоте, обусловленной перемещением подвешенного груза.снижение поперечной метацентрической высоты от влияния перекатывающегося груза будет равно

. (29)

Его можно также трактовать, как результат переноса ЦТ груза в точку ^ A — центр кривизны кривой BB ₁. Следовательно, изменение аппликаты ЦТ судна равно

. (30)

1. 
   Жидкий груз

Пусть на судне в цистерне, танке или отсеке имеется какой-либо жидкий груз. Если этот груз заполняет емкость, например, отсек, целиком, то при наклонении судна он переливаться не будет, его ЦТ останется на месте и в расчете остойчивости такой груз может рассматриваться как твердый. Если же груз заполняет отсек лишь частично и жидкость в отсеке имеет свободную поверхность, то при наклонении судна она будет переливаться, ЦТ груза сместится и это вызовет перемещение ЦТ судна. Ясно, что остойчивость судна при этом изменится.

Рассмотрим вначале наклонение судна на угол в поперечной плоскости (рис. 2, в). Введем обозначения: — объем жидкости в отсеке, — ее плотность, — объемное водоизмещение судна, — плотность забортной воды;;.

Величина дополнительного кренящего момента при переливании груза будет определяться по формуле

. (31)

Если бы груз p находился на судне, не имея возможности переливаться, как бы затвердев, то восстанавливающий момент согласно метацентрической формуле остойчивости был бы равен. При переливании груза он уменьшится на величину дополнительного кренящего момента и будет равен

, (32)

где

(33)

представляет собой поправку к поперечной метацентрической высоте, учитывающую влияние свободной поверхности жидкого груза в отсеке на начальную остойчивость. Все величины, входящие в левую часть (33), положительны, поэтому поправка всегда отрицательна. Таким образом, жидкий груз со свободной поверхностью всегда уменьшаетначальную остойчивость судна. Важно отметить, что поправка не зависит от объема жидкости в отсеке; она зависит от момента инерции площади свободной поверхности и воз растает с его увеличением. Эта поправка тем больше, чем больше соотношение плотностей жидкости в отсеке и забортной воды. Если груз, например разжиженный железорудный концентрат, имеет плотность, значительно большую, чем у воды, остойчивость судна может существенно снизиться даже при сравнительно небольшой площади свободной поверхности.

В случае, когда жидкие грузы со свободными поверхностями имеются в нескольких отсеках или цистернах, дополнительные кренящие моменты от их переливания суммируются и суммарная поправка к метацентрической высоте равна

, (34)

где m — число отсеков и цистерн, имеющих свободные поверхности жидкостей, которые могут быть различными.

Формула для поперечной метацентрической высоты, исправленной на влияние жидких грузов, имеет вид

. (35)

По аналогии с этим выражением исправленную продольную метацентрическую высоту можно определить как

, (36)

где

. (37)

Здесь i_yn — момент инерции свободной поверхности жидкости в отсеке относительно ее центральной поперечной оси, параллельной оси Oy. Для большинства надводных судов в неповрежденном состоянии поправка много меньше продольной метацентрической высоты H и в практических расчетах ее обычно не учитывают.

Для снижения влияния свободных поверхностей жидких грузов на поперечную остойчивость отсек или цистерну разделяют продольными непроницаемыми переборками. Предположим для простоты, что отсек имеет в плане форму прямоугольника длиной l и шириной b (рис. 3).

Момент инерции свободной поверхности жидкости относительно ее центральной продольной оси в таком отсеке равен. Тогда поправка к метацентрической высоте на влияние свободной поверхности жидкого груза согласно формуле (33) будет равна

.

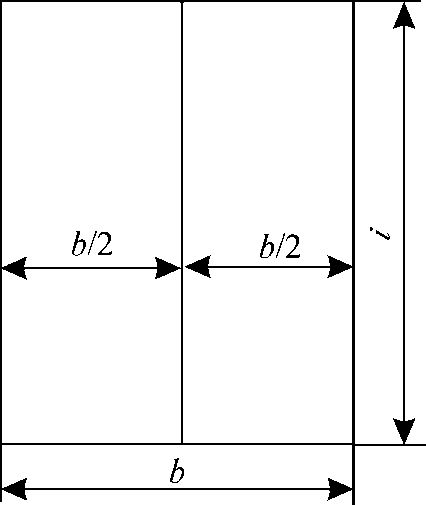
Рис. 3. Отсек с продольной непроницаемой переборкой

Установим посередине отсека продольную непроницаемую переборку. Момент инерции свободной поверхности жидкости в отсеке будет равен сумме моментов инерции двух площадей свободной поверхности шириной b/ 2 каждая:

.

Соответственно поправка к метацентрической высоте

уменьшится в 4 раза. Аналогичным образом легко показать, что при установке двух продольных переборок эта поправка уменьшится в 9 раз, а при установке n переборок в (n + 1)² раз. Таким образом, разделение отсеков с жидкими грузами, имеющими свободную поверхность, непроницаемыми переборками является эффективным средством снижения влияния этих грузов на поперечную остойчивость судна.

При приеме на судно жидкого груза p, координаты ЦТ которого x_p, y_p, z_p, изменение начальной остойчивости должно определяться с учетом влияния свободной поверхности. Добавляя член, учитывающий это влияние в соответствии с (33), получим

,

где (D + p) — сила тяжести судна после приема груза. Подставляя в правую часть этой формулы и вынося за скобку общий множитель, находим

. (38)

Дата добавления: 2015-10-13