Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Решение задачи методом «идеального объекта».

Читайте также:
  1. D) РЕКОНСТРУКЦИЯ И ИНТЕГРАЦИЯ КАК ЗАДАЧИ ГЕРМЕНЕВТИКИ
  2. I. Задачи и методы психологии народов.
  3. II. НАЗНАЧЕНИЕ, ОСНОВНЫЕ ЗАДАЧИ И ФУНКЦИИ ПОДРАЗДЕЛЕНИЯ
  4. II. Разрешение кризиса в Южной Родезии
  5. II. Решите задачи.
  6. II. Цели и задачи Конкурса
  7. II. Цели и задачи Лаборатории

Этап расчета 1. На предварительном этапе отобранная группа принтеров, состоящая из 7 типов принтеров Y={А1, А2, А3, А4, А5, А6, А7}. На основании исходных данных строим матрицу вариантов (табл.17)

Таблица 17

Матрица описания задачи

Принтеры Критерии
К 1 К 2 К 3
А 1      
А 2      
А 3      
А 4      
А 5      
А 6      
А 7      

 

На основании данных приведенных в таблице сформируем «идеальный объект» по указанным критериям со значениями равными максимальным значениям показателей, полезность по которым возрастает, и минимальным полезность по которым убывает. Таким образом, получаем «идеальный объект» А+:

А+ Ì {14; 2; 2776}

Кроме идеального объекта сформируем также модель «наихудшего объекта»:

А- Ì {7; 12; 5830}

Для сопоставления значений критериев необходимо перейти к нормированным единицам, т.к. критерии разнородные, преобразовав их по формуле

aj = (К+-Кj) / (К+- К-).

Переходя к относительным значениям критериев, получим следующую нормализованную матрицу (табл18):

Таблица 18

Нормализованная матрица описания задачи

Принтеры Критерии
К 1 К 2 К 3
А 1 0,29   0,68
А 2 0,86 0,1 0,22
А 3   0,2  
А 4 0,71   0,49
А 5 0,43 0,6 0,55
А 6   0,4  
А 7 0,57 0,6 0,62

 

Зададим относительную важность критериев в виде весов: W1 = 6, W2 = 2, W3 = 4.

Для выявления ненаилучших объектов найдем свертки (расстояние до идеального объекта), используя следующую обобщенную метрику:

Вычислим для наших объектов метрики с разной степенью концентрации, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.19).

Таблица 19

Метрика расстояний по альтернативам

Значения меры расстояния Степень концентрации (р)  
р=1 р=2 р=3 р=5 р=6 р=8
L(А1) 5,56 4,47 4,32 4,29 4,29 4,29
L(А2) 5,78 3,71 3,33 3,17 3,15 3,13
L(А3) 5,60 4,31 4,08 4,01 4,00 4,00
L(А4) 5,76 3,33 2,78 2,42 2,34 2,24
L(А5) 6,04 3,96 3,60 3,46 3,44 3,43
L(А6) 7,20 6,12 6,02 6,00 6,00 6,00
L(А7) 4,89 3,09 2,76 2,61 2,59 2,58

 

Чем больше значение L, тем ближе объект Аi к идеальному А+. Получим следующие ранжировки предпочтений по L.

Для р=1 А6>А5>А2>А4>А3>А1>А7

Для р=2 А6>А1>А3>А5>А2>А4>А7

Для р=3 А6>А1>А3>А5>А2>А4>А7

Для р=5 А6>А1>А3>А5>А2>А7>А4

Для р=6 А6>А1>А3>А5>А2>А7>А4

Для р=8 А6>А1>А3>А5>А2>А7>А4.

Ненаилучшие решения в нашем случае – А4 и А7. Исключим их из рассмотрения, получив сокращенное исходное множество альтернатив {А1, А2, А3, А5, А6}.

Рассмотрим компьютерное решение данного фрагмента задачи в системе Excel.

Экранная форма комплекса таблиц расчета по первому этапу приведена на рис.14.

 

 

Рис. 14. Экранная форма комплекса таблиц расчета по 1 этапу

 

Алгоритм формирования матрицы описания задачи и расчета нормализованной матрицы приведены по 1 этапу приведены в табл.20-21. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 20, в координатах граф и строк, это - диапазон B12:D12 для выбора значений идеального варианта, B13:D13 – для выбора значений наихудшего варианта). В табл.21 приводятся формулы расчета нормализованных значений критериев по альтернативам.

 

Таблица 20. Матрица описания задачи

  А B C D
  Принтеры Критерии
  К 1 К 2 К 3
  А 1      
  А 2      
  А 3      
  А 4      
  А 5      
  А 6      
  А 7      
  идеальный объект А+ =МАКС(B5:B11) =МИН(C5:C11) =МИН(D5:D11)
  наихудший объект А- =МИН(B5:B11) =МАКС(C5:C11) =МАКС(D5:D11)

 

 

Таблица 21. Нормализованная матрица описания задачи

  А B C D
     
  К1 К2 К3
  А1 =(B12-B5)/(B12-B13) =(C12-C5)/(C12-C13) =(D12-D5)/(D12-D13)
  А2 =(B12-B6)/(B12-B13) =(C12-C6)/(C12-C13) =(D12-D6)/(D12-D13)
  А3 =(B12-B7)/(B12-B13) =(C12-C7)/(C12-C13) =(D12-D7)/(D12-D13)
  А4 =(B12-B8)/(B12-B13) =(C12-C8)/(C12-C13) =(D12-D8)/(D12-D13)
  А5 =(B12-B9)/(B12-B13) =(C12-C9)/(C12-C13) =(D12-D9)/(D12-D13)
  А6 =(B12-B10)/(B12-B13) =(C12-C10)/(C12-C13) =(D12-D10)/(D12-D13)
  А7 =(B12-B11)/(B12-B13) =(C12-C11)/(C12-C13) =(D12-D11)/(D12-D13)
  W (важность критерия)      

 

В табл.22 приводятся формулы расчета расстояния по нормализованным значениям для различных степеней концентрации, в частности, для р = 2, имеем Евклидово расстояние. В строке 31 дается линейка коэффициентов концентрации от 1 до 8.

 

 


 

Таблица 22. Матрица расстояний для 1 этапа расчета оценок приоритетов альтернатив

  А B C D E F G
  значения меры расстояния степень концентрации, р  
  а            
  L(А1) =СТЕПЕНЬ(((B26*(1-B19))^B31+(C26*(1-C19))^B31+(D26*(1-D19))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B19))^C31+(C26*(1-C19))^C31+(D26*(1-D19))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-B19))^D31+(C26*(1-C19))^D31+(D26*(1-D19))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B19))^E31+(C26*(1-C19))^E31+(D26*(1-D19))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B19))^F31+(C26*(1-C19))^F31+(D26*(1-D19))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B19))^G31+(C26*(1-C19))^G31+(D26*(1-D19))^G31);1/G31)
  L(А2) =СТЕПЕНЬ(((B26*(1-B20))^B31+(C26*(1-C20))^B31+(D26*(1-D20))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B20))^C31+(C26*(1-C20))^C31+(D26*(1-D20))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-B20))^D31+(C26*(1-C20))^D31+(D26*(1-D20))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B20))^E31+(C26*(1-C20))^E31+(D26*(1-D20))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B20))^F31+(C26*(1-C20))^F31+(D26*(1-D20))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B20))^G31+(C26*(1-C20))^G31+(D26*(1-D20))^G31);1/G31)
  L(А3) =СТЕПЕНЬ(((B26*(1-B21))^B31+(C26*(1-C21))^B31+(D26*(1-D21))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B21))^C31+(C26*(1-C21))^C31+(D26*(1-D21))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B21))^D31+(C26*(1-$C21))^D31+(D26*(1-$D21))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B21))^E31+(C26*(1-C21))^E31+(D26*(1-D21))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B21))^F31+(C26*(1-C21))^F31+(D26*(1-D21))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B21))^G31+(C26*(1-C21))^G31+(D26*(1-D21))^G31);1/G31)
  L(А4) =СТЕПЕНЬ(((B26*(1-B22))^B31+(C26*(1-C22))^B31+(D26*(1-D22))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B22))^C31+(C26*(1-C22))^C31+(D26*(1-D22))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B22))^D31+(C26*(1-$C22))^D31+(D26*(1-$D22))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B22))^E31+(C26*(1-C22))^E31+(D26*(1-D22))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B22))^F31+(C26*(1-C22))^F31+(D26*(1-D22))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B22))^G31+(C26*(1-C22))^G31+(D26*(1-D22))^G31);1/G31)
  L(А5) =СТЕПЕНЬ(((B26*(1-B23))^B31+(C26*(1-C23))^B31+(D26*(1-D23))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B23))^C31+(C26*(1-C23))^C31+(D26*(1-D23))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B23))^D31+(C26*(1-$C23))^D31+(D26*(1-$D23))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B23))^E31+(C26*(1-C23))^E31+(D26*(1-D23))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B23))^F31+(C26*(1-C23))^F31+(D26*(1-D23))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B23))^G31+(C26*(1-C23))^G31+(D26*(1-D23))^G31);1/G31)
  L(А6) =СТЕПЕНЬ(((B26*(1-B24))^B31+(C26*(1-C24))^B31+(D26*(1-D24))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B24))^C31+(C26*(1-C24))^C31+(D26*(1-D24))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B24))^D31+(C26*(1-$C24))^D31+(D26*(1-$D24))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B24))^E31+(C26*(1-C24))^E31+(D26*(1-D24))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B24))^F31+(C26*(1-C24))^F31+(D26*(1-D24))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B24))^G31+(C26*(1-C24))^G31+(D26*(1-D24))^G31);1/G31)
  L(А7) =СТЕПЕНЬ(((B26*(1-B25))^B31+(C26*(1-C25))^B31+(D26*(1-D25))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B25))^C31+(C26*(1-C25))^C31+(D26*(1-D25))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B25))^D31+(C26*(1-$C25))^D31+(D26*(1-$D25))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B25))^E31+(C26*(1-C25))^E31+(D26*(1-D25))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B25))^F31+(C26*(1-C25))^F31+(D26*(1-D25))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B25))^G31+(C26*(1-C25))^G31+(D26*(1-D25))^G31);1/G31)

 

 


Этап расчета 2. На втором этапе, по усеченному множеству альтернатив (табл.23) опять строим идеальный А+ и наихудший А- варианты.

Таблица 23

Матрица описания задачи

по сокращенному множеству альтернатив

Принтеры Критерии
К 1 К 2 К 3
А 1      
А 2      
А 3      
А 5      
А 6      

 

Значение параметров крайних альтернатив следующие:

Принтеры Критерии
К 1 К 2 К 3
идеальный объект А+      
наихудший объект А-      

 

Для сопоставления значений критериев также необходимо перейти к нормированным единицам, т.к. критерии разнородные, опять преобразовав их по формуле

aj = (К+-Кj) / (К+- К-).

Переходя к относительным значениям критериев, получим новую нормализованную матрицу (табл.24).

Таблица 24

Нормализованная матрица описания задачи

по сокращенному множеству альтернатив

Принтеры Критерии
К 1 К 2 К 3
А 1 0,29   0,68
А 2 0,86   0,22
А 3   0,11  
А 5 0,43 0,56 0,55
А 6   0,33  

 

Также зададим относительную важность критериев в виде весов: W1=6, W2=2, W3=4.

Для выявления не наилучших объектов найдем свертки (расстояние до идеального объекта), используя метрику:

Вычислим для наших объектов разные метрики, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.25).

Таблица 25

Метрика расстояний по альтернативам

Значения меры расстояния Степень концентрации (р)  
р=1 р=2 р=3 р=5 р=6 р=8
L(А1) 5,56 4,47 4,32 4,29 4,29 4,29
L(А2) 5,98 3,81 3,40 3,19 3,16 3,14
L(А3) 5,78 4,38 4,11 4,01 4,01 4,00
L(А5) 6,12 3,98 3,61 3,46 3,44 3,43
L(А6) 7,33 6,15 6,02 6,00 6,00 6,00

 

Чем больше значение L, тем ближе объект Аi к идеальному А+. Получим следующие ранжировки предпочтений по L.

Для р=1 А6>А5>А2>А3>А1

Для р=2 А6>А1>А3>А5>А2

Для р=3 А6>А1>А3>А5>А2

Для р=5 А6>А1>А3>А5>А2

Для р=6 А6>А1>А3>А5>А2

Для р=8 А6>А1>А3>А5>А2

Ненаилучшие решения в нашем случае – А2 и А5. Исключим их из рассмотрения, получив сокращенное исходное множество {А1, А3, А6}. Рассмотрим компьютерное решение данного фрагмента (2 уровня) решения задачи в системе Excel.

Экранная форма комплекса таблиц расчета по второму этапу приведена на рис.15.

 

 

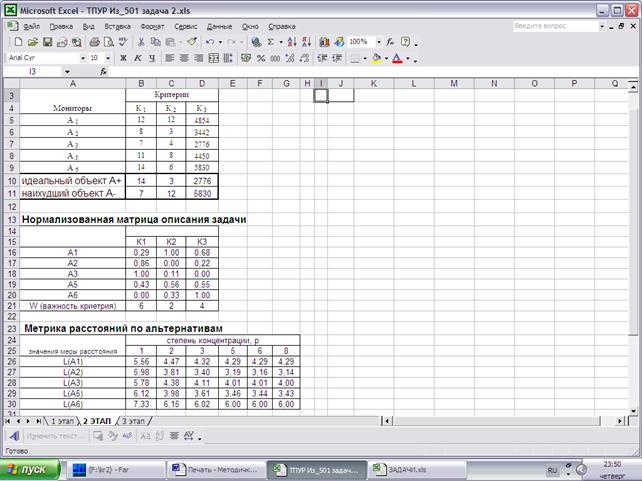
Рис.15. Экранная форма комплекса таблиц расчета по 2 этапу решения задачи

 

Алгоритм формирования матрицы описания усеченной задачи и расчета нормализованной матрицы приведены по 2 этапу приведены в табл.26-27. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 26, в координатах граф и строк, это - диапазон B10:D10 для выбора значений идеального варианта, B11:D11 – для выбора значений наихудшего варианта). В табл.27 приводятся формулы расчета нормализованных значений критериев по альтернативам.

Таблица 26

Матрица описания задачи (2 этап)

  A B C D  
  Принтеры Критерии  
  К 1 К 2 К 3  
  А 1        
  А 2        
  А 3        
  А 5        
  А 6        
  идеальный объект А+ =МАКС(B5:B9) =МИН(C5:C9) =МИН(D5:D9)
  наихудший объект А- =МИН(B5:B9) =МАКС(C5:C9) =МАКС(D5:D9)

 

 

Таблица 27.

Нормализованная матрица описания задачи

  A B C D
     
  К 1 К 2 К 3
  А1 =(B10-B5)/(B10-B11) =(C10-C5)/(C10-C11) =(D10-D5)/(D10-D11)
  А2 =(B10-B6)/(B10-B11) =(C10-C6)/(C10-C11) =(D10-D6)/(D10-D11)
  А3 =(B10-B7)/(B10-B11) =(C10-C7)/(C10-C11) =(D10-D7)/(D10-D11)
  А5 =(B10-B8)/(B10-B11) =(C10-C8)/(C10-C11) =(D10-D8)/(D10-D11)
  А6 =(B10-B9)/(B10-B11) =(C10-C9)/(C10-C11) =(D10-D9)/(D10-D11)
  W (важность критерия)      

 

В табл.28 приводятся формулы расчета расстояния по нормализованным значениям усеченной матрицы альтернатив для различных степеней концентрации.

 


Таблица 28

Метрика расстояний по альтернативам (2 этап)

  А B C D E F G
  значения меры расстояния степень концентрации, р  
  а            
  L(А1) =СТЕПЕНЬ(((B26*(1-B19))^B31+(C26*(1-C19))^B31+(D26*(1-D19))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B19))^C31+(C26*(1-C19))^C31+(D26*(1-D19))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-B19))^D31+(C26*(1-C19))^D31+(D26*(1-D19))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B19))^E31+(C26*(1-C19))^E31+(D26*(1-D19))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B19))^F31+(C26*(1-C19))^F31+(D26*(1-D19))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B19))^G31+(C26*(1-C19))^G31+(D26*(1-D19))^G31);1/G31)
  L(А2) =СТЕПЕНЬ(((B26*(1-B20))^B31+(C26*(1-C20))^B31+(D26*(1-D20))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B20))^C31+(C26*(1-C20))^C31+(D26*(1-D20))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-B20))^D31+(C26*(1-C20))^D31+(D26*(1-D20))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B20))^E31+(C26*(1-C20))^E31+(D26*(1-D20))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B20))^F31+(C26*(1-C20))^F31+(D26*(1-D20))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B20))^G31+(C26*(1-C20))^G31+(D26*(1-D20))^G31);1/G31)
  L(А3) =СТЕПЕНЬ(((B26*(1-B21))^B31+(C26*(1-C21))^B31+(D26*(1-D21))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B21))^C31+(C26*(1-C21))^C31+(D26*(1-D21))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B21))^D31+(C26*(1-$C21))^D31+(D26*(1-$D21))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B21))^E31+(C26*(1-C21))^E31+(D26*(1-D21))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B21))^F31+(C26*(1-C21))^F31+(D26*(1-D21))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B21))^G31+(C26*(1-C21))^G31+(D26*(1-D21))^G31);1/G31)
  L(А5) =СТЕПЕНЬ(((B26*(1-B23))^B31+(C26*(1-C23))^B31+(D26*(1-D23))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B23))^C31+(C26*(1-C23))^C31+(D26*(1-D23))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B23))^D31+(C26*(1-$C23))^D31+(D26*(1-$D23))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B23))^E31+(C26*(1-C23))^E31+(D26*(1-D23))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B23))^F31+(C26*(1-C23))^F31+(D26*(1-D23))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B23))^G31+(C26*(1-C23))^G31+(D26*(1-D23))^G31);1/G31)
  L(А6) =СТЕПЕНЬ(((B26*(1-B24))^B31+(C26*(1-C24))^B31+(D26*(1-D24))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B24))^C31+(C26*(1-C24))^C31+(D26*(1-D24))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B24))^D31+(C26*(1-$C24))^D31+(D26*(1-$D24))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B24))^E31+(C26*(1-C24))^E31+(D26*(1-D24))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B24))^F31+(C26*(1-C24))^F31+(D26*(1-D24))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B24))^G31+(C26*(1-C24))^G31+(D26*(1-D24))^G31);1/G31)

 


Этап расчета 3. На третьем этапе также строим идеальный А+ {14; 4; 2776} и наихудший А- { 7; 12; 5830} варианты уже по усеченному множеству (до 3) альтернатив (табл.29).

Таблица 29

Матрица описания задачи

по сокращенному множеству альтернатив

Принтеры Критерии
К1 К2 К3
А1      
А3      
А6      

 

Определяем значения параметров крайних альтернатив:

 

Принтеры Критерии
К 1 К 2 К 3
идеальный объект А+      
наихудший объект А-      

 

Для сопоставления значений критериев необходимо перейти к нормированным единицам, т.к. критерии разнородные, преобразовав их по формуле

aj = (К+-Кj) / (К+- К-).

Переходя к относительным значениям критериев, получим новую нормализованную матрицу (табл.30).

Таблица 30

Нормализованная матрица описания задачи

по сокращенному множеству альтернатив

Принтеры Критерии
К1 К2 К3
А1 0,29   0,68
А3      
А6   0,25  

 

Опять зададим относительную важность критериев в виде весов:W1 = 6, W2 = 2, W3 =4.

Для выявления ненаилучших вариантов найдем метрические свертки (расстояние до идеального варианта), используя следующую метрику:

Вычислим для наших объектов разные метрики, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.31).

Таблица 31

Метрика расстояний по сокращенному количеству альтернативам

Значения меры расстояния Степень концентрации (р)  
р=1 р=2 р=3 р=5 р=6 р=8
L(А1) 5,56 4,4723 4,32 4,29 4,29 4,29
L(А3) 6,00 4,4721 4,16 4,02 4,01 4,00
L(А6) 7,50 6,18 6,03 6,00 6,00 6,00

 

Чем больше значение L, тем ближе объект Аi к идеальному А+. Получим следующие ранжировки предпочтений по L.

Для р=1 А6>А3>А1

Для р=2 А6>А1>А3

Для р=3 А6>А1>А3

Для р=5 А6>А1>А3

Для р=6 А6>А1>А3

Для р=8 А6>А1>А3

 

Ненаилучшие решения в нашем случае – А1 и А3. Остался один доминирующий объект А6, т.е. это и есть наилучшее решение в нашей ситуации.

Компьютерное решение данного фрагмента (3 уровня) решения приведено на рис.16.

 

 

Рис.16. Экранная форма комплекса таблиц расчета по 3 этапу решения задачи

 

Алгоритм формирования матрицы описания усеченной до 3 альтернатив задачи и расчета нормализованной матрицы по 3 этапу приведены в табл.32-33. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 32, в координатах граф и строк, это - диапазон B8:D8 для выбора значений идеального варианта, B9:D9 – для выбора значений наихудшего варианта). В табл.33 приводятся формулы расчета нормализованных значений критериев по альтернативам.

 

 

Таблица 32

Матрица описания задачи (3 этап)

  А B C D  
  Принтеры Критерии  
  К 1 К 2 К 3  
  А 1        
  А 3        
  А 6        
  идеальный объект А+ =МАКС(B5:B11) =МИН(C5:C11) =МИН(D5:D11)
  наихудший объект А- =МИН(B5:B11) =МАКС(C5:C11) =МАКС(D5:D11)  

 

Таблица 33

Нормализованная матрица описания задачи

  A B C D
    Критерии
  К 1 К 2 К 3
  А1 =(B10-B5)/(B10-B11) =(C10-C5)/(C10-C11) =(D10-D5)/(D10-D11)
  А3 =(B10-B7)/(B10-B11) =(C10-C7)/(C10-C11) =(D10-D7)/(D10-D11)
  А6 =(B10-B9)/(B10-B11) =(C10-C9)/(C10-C11) =(D10-D9)/(D10-D11)
  W (важность критерия)      

 

В табл.34 приводятся формулы расчета расстояния по нормализованным значениям усеченной матрицы альтернатив для различных степеней концентрации.

 

 


 

Таблица 34

Метрика расстояний по альтернативам (3 этап)

  А B C D E F G
  значения меры расстояния степень концентрации, р  
  а            
  L(А1) =СТЕПЕНЬ(((B26*(1-B19))^B31+(C26*(1-C19))^B31+(D26*(1-D19))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B19))^C31+(C26*(1-C19))^C31+(D26*(1-D19))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-B19))^D31+(C26*(1-C19))^D31+(D26*(1-D19))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B19))^E31+(C26*(1-C19))^E31+(D26*(1-D19))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B19))^F31+(C26*(1-C19))^F31+(D26*(1-D19))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B19))^G31+(C26*(1-C19))^G31+(D26*(1-D19))^G31);1/G31)
  L(А3) =СТЕПЕНЬ(((B26*(1-B21))^B31+(C26*(1-C21))^B31+(D26*(1-D21))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B21))^C31+(C26*(1-C21))^C31+(D26*(1-D21))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B21))^D31+(C26*(1-$C21))^D31+(D26*(1-$D21))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B21))^E31+(C26*(1-C21))^E31+(D26*(1-D21))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B21))^F31+(C26*(1-C21))^F31+(D26*(1-D21))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B21))^G31+(C26*(1-C21))^G31+(D26*(1-D21))^G31);1/G31)
  L(А6) =СТЕПЕНЬ(((B26*(1-B24))^B31+(C26*(1-C24))^B31+(D26*(1-D24))^B31);1/B31) =СТЕПЕНЬ(((B26*(1-B24))^C31+(C26*(1-C24))^C31+(D26*(1-D24))^C31);1/C31) =СТЕПЕНЬ(((B26*(1-$B24))^D31+(C26*(1-$C24))^D31+(D26*(1-$D24))^D31);1/D31) =СТЕПЕНЬ(((B26*(1-B24))^E31+(C26*(1-C24))^E31+(D26*(1-D24))^E31);1/E31) =СТЕПЕНЬ(((B26*(1-B24))^F31+(C26*(1-C24))^F31+(D26*(1-D24))^F31);1/F31) =СТЕПЕНЬ(((B26*(1-B24))^G31+(C26*(1-C24))^G31+(D26*(1-D24))^G31);1/G31)

 

 


2.3.5. Задачи JA – класса (неструктурированные критерии),

Дата добавления: 2015-10-13; просмотров: 78 | Нарушение авторских прав

Читайте в этой же книге: Тема 8. Автоматизация процедур принятия решений | Структура контрольной работы | Краткая характеристика и классификация задач | Методология решения задач группового выбора | Задачи J - класса | Продукт 3 не может выпускаться в количестве, превышающем 2,4. | Решение задачи линейной оптимизации в интегрированных системах | Microsoft Excel 7.0 Отчет по результатам | Принцип максимина (гарантированного результата) | Решение задачи по принципу Гурвица. |
<== предыдущая страница | следующая страница ==>
Решение задачи по принципу Сэвиджа.| Решаемую лексикографическим методом
mybiblioteka.su - 2015-2024 год. (0.032 сек.)