Решение задачи линейной оптимизации в интегрированных системах

Решение этой задачи рассмотрим на примере использования модуля математического анализа данных интегрированной системы (табличного процессора) Excel 7.0, который позволяет решать подобные оптимизационные задачи.

Рассмотрим решение задач линейного программирования на следующем примере.

Пример решения. Планом развития региона предполагается ввести в действие 3 нефтяных месторождения с суммарным объемом добычи равным 9 млн.т. На первом месторождении объем добычи составляет не менее 1 млн.т, на втором - 3 млн. т, на третьем - 5 млн.т. Для достижения такой производительности необходимо пробурить не менее 125 скважин. Для реализации данного плана выделено 25 млн. руб. капитальных вложений (показатель К) и 80 км труб (показатель L).

Требуется определить оптимальное (максимальное) количество скважин для обеспечения плановой производительности каждого месторождения.

Исходные данные по задаче приведены в табл.8

Таблица 8

Исходные данные

Место-рождение	Добыча, млн.т	Фонд скважин	Дебет 1 скважи-ны	Длина трубо-провода для 1 скважины	Стоимость строительства 1 скважины	K	L
				1.0 2.0 0.5
Итого:						25.0	80.0

Постановка задачи.

Целью решения данной оптимизационной задачи является нахождение максимального значения добычи нефти при оптимальном количестве скважин по каждому месторождению с учетом существующих ограничений по задаче.

Целевая функция в соответствии с требованиями задачи примет вид:

.

где - количество скважин по каждому месторождению.

Существующие ограничения по задаче на:

* длину прокладки труб:

;

* число скважин на каждом месторождении:

X₁ £ 10,

X₂ £ 15,

X₃ £ 100;

* стоимость строительства 1 скважины:

.

Решение задачи. Ввести в электронную таблицу Excel 7.0 данные.

¨ в ячейку B11 поместить целевую функцию C7*C9+D7*D9+E7*E9;

¨ начальные значения искомых переменных поместить в ячейки с адресами: С9, D9, E9;

¨ значения единичной добычи поместить в ячейки С7, D7, E7;

¨ значения протяженности трубопровода для строительства одной скважины ввести в ячейки ЭТ: С5, D5, E5;

¨ стоимость строительства скважины - в ячейки С6, D6, E6;

¨ формулу расчета общей протяженности C5*C9+D5*D9+E5*E9 поместить в ячейку В5;

¨ формулу расчета общей стоимости C6*C9+D6*D9+E6*E9 сформировать в ячейке B6;

¨ тип ограничений - в ячейки F5, F6;

¨ значения ограничений - в ячейки G5, G6;

¨ ограничения количества скважин С8, D8, E8.

Исходные данные для решения задачи отображены в табл.на рис.3.

Для решения оптимизационных задач в ЭТ используется команда «Поиск решения» в меню «Сервис».

Следует заметить, что программа «Поиск решения» оперирует с тремя основными компонентами построенной в ЭТ оптимизируемой модели:

Рис.3. Исходные данные для решения

Постановка задачи осуществляется в диалоговом окне «Поиск решения» (рис.4).

Рис. 4. Диалоговое окно «Поиск решения»

à ячейкой, содержащей целевую функцию задачи (в таблице на рис.3 это - ячейка В11);

à изменяемыми ячейками, содержащими независимые переменные (в таблице на рис.3 это - ячейки C9:E9);

à ячейками, содержащими левые части ограничений на имеющиеся ресурсы, а также простые ограничения на независимые переменные (в табл. 7 это - ячейки F5:G6).

В поле «Установить целевую ячейку» нужно указать адрес ячейки, которая содержит формулу для расчета целевой функции. Очень важно, чтобы эта формула была связана с изменяемыми ячейками, выражающими искомые переменные задачи (объемы производства различных типов продукции).

В поле «Изменяя ячейки» ввести область, содержащую изменяемые ячейки.

Для того, чтобы задать ограничения, следует нажать кнопку «Добавить». Появится диалоговое окно - «Добавление ограничения» (рис.5).

Рис.5. Диалоговое окно «Добавление ограничения»

В левом поле диалогового окна «Добавление ограничения» указывают адрес ячейки, содержимое которой должно удовлетворять заданному ограничению. В правом поле задают значение ограничения или указывают адрес ячейки, где такое значение содержится (в данном случае 10 или С8). В поле, находящемся между этими двумя полями, справа от которого расположена кнопка со стрелкой, задают оператор, который определяет соотношение между содержимым ячейки, указанном в левом поле, и заданным в правом поле ограничением.

В этом примере необходимо задать 5 ограничений.

После того как ввели первое ограничение, нажатием кнопки «Добавить» можно ввести значение без закрытия диалогового окна «Добавление ограничения». После закрытия окна «Добавление ограничения» в поле «Ограничения» окна «Поиск решения» появятся все введенные ограничения.

После того, как все ограничения для программы «Поиск решения» заданы, можно воспользоваться кнопками «Изменить» и «Удалить» для изменения или удаления ряда ограничений из их списка.

Дополнительные параметры, определяющие способ выполнения вычислений, можно задать в диалоговом окне «Параметры поиска решения» (рис 6). Это окно открывается нажатием на кнопку «Параметры» в диалоговом окне «Поиск решения».

Рис. 6. Диалоговое окно «Параметры поиска решения»

Решаемая задача относится к линейным, поэтому указываем способ вычислений «Линейная модель», отметим флажком данное поле и ОК.

Запустите процесс вычислений нажатием кнопки «Выполнить». В строке состояния будут отображены некоторые шаги процесса вычислений. После того, как поиск решения завершен, новые значения будут вставлены в таблицу, а на экране появится диалоговое окно «Результаты поиска решения», которое будет содержать информацию о завершении процесса поиска решения (рис. 7). Здесь можно указать, должен ли быть представлен в таблице новый результат и нужно ли составить отчет.

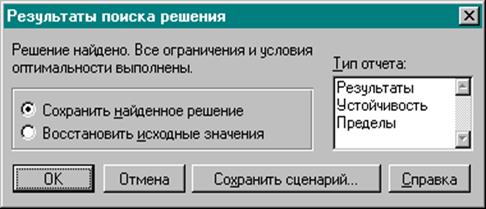
Рис.7. Диалоговое окно «Результаты поиска решения»

Если установлена опция «Восстановить исходные значения» и не задано составление отчета, то найденные значения будут удалены. При задании режима составления отчета следует выбрать тип отчета в поле «Тип отчета» и ОК.

Таким образом, программа выполнила расчет определения оптимального (максимального) количества скважин для обеспечения плановой производительности каждого месторождения (таблица на рис. 8).

Рис.8. Таблица с результатами решения

Очень часто на практике необходимо исследовать полученное решение, чтобы получить ответы на целый ряд возникающих при изучении решения вопросов. Например, если интересует чувствительность полученных оптимальных решений к изменению различных параметров исходной модели, то в этом могут помочь предлагаемые в окне «Поиск решения» отчеты: отчет по результатам, отчет по устойчивости и отчет по пределам.

Отчет по результатам. На рис.9 представлен отчет по результатам, включающий в себя три таблицы.

Дата добавления: 2015-10-13