Принцип минимума усредненного риска

Пусть, как и в п. 4.3.1, на множестве P задана некоторая мера 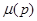и определен функционал 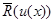(4.3.2), представляющий собой усред­ненный по этой мере средний риск . Один из возможных принципов предпочтения заключается в выборе правила решения , ми­нимизирующего этот усредненный результат, то есть удовлетворяющего соотношению

. (4.3.8)

Неоднозначность выбора решения при таком подходе связана только с неоднозначностью меры 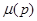. Последней может быть придана раз­личная трактовка - как невероятностная, так и вероятностная.

Прежде всего 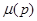можно рассматривать как меру, характеризую­щую значимость последствий от принятия решения в данных условиях, соответствующих конкретному значению 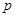. При этом - относи­тельный вес риска принятия решения при условии, что статистические данные задачи описываются распределением 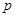, то есть величина, характе­ризующая относительную важность средних потерь в этих условиях. Представление о такой относительной важности обычно всегда имеется, причем часто оно сводится к представлению об одинаковой значимости потерь, которое естественно приводит к тому, что мера 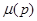соответст­вует равномерному распределению на множестве P.

В то же время 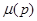формально может рассматриваться (при соот­ветствующей нормировке) как некоторое априорное распределение на множестве P. При такой трактовке задача вновь становится чисто байесовой с распределением вероятности х и , задаваемом плотностью

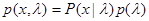; . (4.3.9)

Несмотря на полное формальное совпадение результатов примене­ния двух этих трактовок, они глубоко различаются по своей сущности. В первом случае устранение априорной неопределенности достигается приписыванием того или иного веса потерям от принятия решения в различных условиях, соответствующих различным 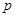, и для такого взвешивания обычно имеется субъективная и объективная основы. Во втором случае априорная неопределенность устраняется заданием веро­ятностей появления различных 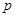. При этом могут быть использованы различные соображения: например, о равных возможностях появления различных 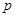(то есть задание равномерного распределения на P) или более слабое предположение об относительно медленном изменении при переходе от одного элемента множества P к другому. Наконец, можно задать наименее предпочтительную меру 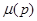, для которой достигается

, (4.3.10)

то есть использовать при ее задании принцип максимина.

Правило решения , определенное из условия минимума усред­ненного риска (4.3.8), очевидно, обладает следующим свойством:

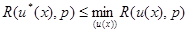, (4.3.11)

которое следует из соотношения

. (4.3.12)

и неотрицательности , то есть оно не лучше байесова правила реше­ния при известной статистике (известном 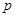). В то же время, как уже отмечалось в п. 4.3.1, этот принцип обеспечивает получение равномерно наилучшего правила решения, если оно существует. То же верно и в от­ношении приближенного равномерно наилучшего правила решения. Принцип минимизации усредненного риска в отличие от минимаксиминного принципа в полной мере использует все данные наблюдения х с учетом их возможной избыточности для устранения неопределенности, связанной с неполным исходным статистическим описанием задачи.

4.3.5. Минимаксный принцип

Если существование точного или приближенного равномерно наи­лучшего правила решения, оправдывающее задание более или менее произвольной меры 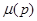, проблематично, а других оснований для за­дания 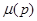нет, то разумным принципом предпочтения при выборе ре­шения является принцип минимакса, согласно которому правило реше­ния 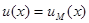выбирается так, чтобы обеспечить

. (4.3.13)

Этот принцип гарантирует, что при всех P величина среднего риска для правила решения 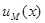будет не больше величины, определяемой. выражением (4.3.13), то есть во всем диапазоне условий, характерном для данного уровня априорной неопределенности, средний риск не превысит величины (4.3.13).

Характерной и иногда неприятной особенностью минимаксного пра­вила решения 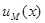является то, что для него средний риск 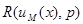может достигать своего максимума не в единственной точке 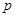, а на не­котором подмножестве P₁ множества P, а иногда и на всем множестве P. В связи с этим, вообще говоря, более предпочтительным может ока­заться выбор такого решения, для которого

и даже на некотором подмножестве множества P

,

но зато на остающейся части множества P

,

причем для многих P существенно меньше.

Вторая особенность минимаксного принципа - возможная неодно­значность в выборе правила решения 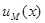. Вид поверхности , иллюстрирующий эту возможность, показан на рис. 4.3, где имеется целое множество минимаксных решений. Для выбора между ни­ми необходим дополнительный критерий, в качестве которого целесо­образно и удобно использовать критерий минимума усредненного риска (для сохранения гарантированного уровня риска (4.3.13) его минимиза­цию следует проводить по ).

Минимаксный принцип, в отличие от рассмотренных ранее, совсем не требует для устранения влияния апри­орной неопределенности привлечения каких-либо дополнительных сообра­жений (существования равномерно наилучшего правила решения, асимптотической сходимости, дополнитель­ной меры 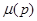), и в этом смысле он яв­ляется наиболее аккуратным, поскольку оперирует только непосред­ственно с основными данными задачи. Степень влияния априорной неопреде­ленности может быть оценена разницей между рисками минимаксного правила решения и байесова с изве­стным распределением 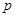, то есть величиной

. (4.3.14)

Если для всех P , где - заданная степень допусти­мого отклонения риска от риска абсолютно оптимального байесова пра­вила решения, то минимаксное правило решения вполне удовлетвори­тельно, а влияние априорной неопределенности на величину риска не превышает .

Рис. 4.3. Вид поверхности среднего риска для различных и P

Дата добавления: 2015-09-03