Простое обучение

1. Самый простой случай эмпирической статистики - это случай, когда в серии из N независимых наблюдений получены значения , где каждая из составляющих тождественна с точки зрения объема и содержания наблюдаемых данных величине х, получаемой в рабочей ситуации, а значения для известны. В этом случае любая из составляющих совокупности эмпирических дан­ных представляет собой пару , где под­чиняется тому же условному распределению вероятности (полностью или частично неизвестному), что и х. Совместное условное распределе­ние вероятности для совокупности значений иданных наблю­дения х в рабочей ситуации может быть описано плотностью вероят­ности

, (3.3.1)

где - всюду одна и та же функция; известны,
а , определяющая величину потерь в рабочей ситуации, неизвестна. В частном случае дискретного множества значений () последовательность иногда удобно разбить на последователь­ности (), соответству­ющие имеющимся эмпирическим данным для каждого из значений 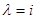. Заметим, что случай, когда на каждом -м шаге в процессе эмпириче­ского набора данных наряду с результатом наблюдения становится известным и истинное состояние ситуации, характеризуемое параметра­ми , называется иногда обучением с учителем.

2. Следующий характерный случай, когда каждая из составляющих эмпирической совокупности по-прежнему тождественна по объему и содержанию величине х, но значения параметров неизвестны, то есть истинная ситуация, в которой наблюдается , остается неизвестной. 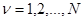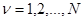При этом также предполагается, что все ситуации для , в ко­торых получены эмпирические данные и рабочая ситуация статистичес­ки однородны, то есть все для и имеют одно и то же распределение вероятности. Совместное распределение вероятности { }и х при заданном значении , для рабочей ситуации в этом случае мо­жет быть описано следующей плотностью:

, (3.3.2)

где 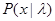- функция правдоподобия (полностью либо частично неиз­вестная), а

, (3.3.3)

- плотность безусловного распределения вероятности х, неопределен­ность которой может быть еще большей, чем функции правдоподобия, из-за частичного либо полного незнания априорного распределения
параметров (плотности ).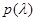

3. Более общий случай имеет место, если в процессе набора эмпи­рических данных наблюдаются величины не обязательно тождественные по объему и содержанию х и , но связанные с ними известной функциональной либо более общей вероятностной зависимостью. Это означает, что любая из составляющих может быть описана услов­ным распределением вероятности с плотностью , которое может быть полностью или частично неизвестным (при наличии функ­циональной зависимости указанная плотность дельтообразна), а пол­ная совокупность эмпирических данных { } и данных наблю­дения х в рабочей ситуации имеет условное (при заданном ) распределение с плотностью вероятности

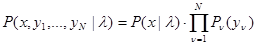, (3.3.4)

где

. (3.3.5)

Величины могут представлять собой, например, отдельные компоненты полного вектора данных наблюдения х (не обязательно одинаковые при разных ), результат наблюдения с дополнительными помехами и ошибками или, наоборот, в лучших по сравнению с рабочей ситуацией условиях и т. п.

Следует отметить, что независимость отдельных составляющих совокупности эмпирических данных, которая использована при записи (3.3.1), (3.3.2), (3.3.4), не имеет принципиального значения. Важно лишь существование той или иной степени статистического подобия между рабочей ситуацией и ситуациями, в которых получены эмпири­ческие данные, а распространение рассуждений на случай зависимости и х сводится лишь к соответствующему изменению формы записи совместных распределений вероятности.

На основании проведенного выше рассмотрения можно зафиксиро­вать несколько существенных моментов.

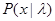а). Совокупность эмпирических данных { } имеет ценность с точки зрения принятия решения в рабочей ситуации только в том слу­чае, если имеется априорная неопределенность относительно статистиче­ского описания х и . Действительно, если и 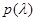известны, то,,
как следует из выражений для среднего и апостериорного риска гл. 2 и выражений (3.3.1), (3.3.2), (3.3.4), расширение полной совокупности данных наблюдения за счет использования эмпирических данных
( }, то есть увеличение входной информации с заменой х на сово­купность { }, не изменяет ни оптимального правила реше­ния и (оно остается зависящим только от х), ни величины
соответствующего ему риска. Это совершенно естественно, поскольку данные прошлых наблюдений { } не содержат непосредственно сведений о значении ненаблюдаемых параметров , определяющих ве­личину потерь от принятия того или иного решения. Если неопределен­ность относится только к априорному распределению вероятности ( 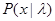известно), не имеют ценности эмпирические данные при обучении с учителем (в этом случае полезны только значения { }, несущие информацию о структуре ).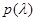

Сформулированные выводы в равной степени относятся как к простому обучению, так и к «рабочеподобному»

б).Для описания частично или полностью неизвестных распределе­ний вероятности совокупности х и эмпирических данных могут быть использованы все обсуждавшиеся в § 3.1, 3.2 методы и, в частности, с успехом применены рассмотренные в § 3.2 методы пара­метрического описания в случае ограниченных априорных значений. При этом эмпирические данные являются источником информации о неизвестных значениях параметров и 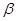функции правдоподобия и априорного распределения вероятности .

в). Наличие эмпирических данных , полученных простым.наблюдением без принятия решения в каждой -й ситуации (простое обучение), нисколько не изменяет исходную постановку задачи стати­стического решения и ее общую формулировку как в байесовом случае, так и при наличии априорной неопределенности. Действительно, так как потери зависят только от значения параметров , в рабочей ситуации (и не зависят от , ), назовем совокупностью данных наблюдения х и то, что мы раньше обозначали этой буквой и вместе с ним все остальные имеющиеся данные, полученные в процессе эмпи­рического изучения статистики, то есть произведем переобозначение . Поскольку конкретное содержание совокупности х не было ограничено, то естественно, что от такого переобозначения ничего не изменится. Поэтому специальное выделение совокупности данных { }, отражающих прошлый опыт, имеет весьма ограни­ченное значение, а терминология, связанная с понятием обучения, мо­жет быть удобна только из-за наглядности рассуждений.

Забегая вперед, необходимо отметить, что этот вывод справедлив и для «рабочеподобного» обучения, если потери во всех ситуациях (), за исключением рабочей, равны нулю или несущественны.

Дата добавления: 2015-09-03