Обучение

Рассмотренные выше аналитические способы неполного статистиче­ского описания х и по существу соответствуют тому, что в каждой конкретной практической задаче создается некоторая аналитическая мо­дель для описания статистических свойств х и с той степенью полноты и подробности, которая соответствует имеющимся знаниям о закономер­ностях их поведения, физических свойствах, взаимосвязи между собой. Подобная модель является в какой-то степени наиболее сжатым опи­санием имеющегося прошлого опыта, содержащего как результаты изу­чения указанных закономерностей, так и, возможно, эмпирические дан­ные относительно х и .

На практике бывает и так, что, кроме эмпирических данных, всякая иная априорная информация относительно х и отсутствует. Однако если эти данные получены в обстановке, статистически однородной или хотя бы статистически связанной с той, в которой принимается решение no данным наблюдения х, то они являются в определенной степени статистическим эквивалентом аналитических моделей для распределе­ний вероятности х и , необходимых для нахождения оптимального правила принятия решения. Степень этой эквивалентности, естественно, зависит от объема имеющихся эмпирических данных, которые, в свою очередь, могут быть использованы по-разному: непосредственно для нахождения недостающих распределений вероятности, для оценки функциональной зависимости апостериорного риска от х и решения u, для уточнения структуры и параметров решающего правила (алгорит­ма обработки данных наблюдения х). Процедуру использования эмпи­рических данных, которые характеризуют прошлый опыт, обычно на­зывают обучением, а соответствующие алгоритмы — обучаемыми.

Для того чтобы яснее представить себе возможный качественный состав имеющихся эмпирических данных и возможные способы их ис­пользования при синтезе систем в условиях априорной неопределенности, предположим, что имеется серия повторяющихся ситуаций, статистически однородных или хотя бы статически связанных с той, в которой мы должны принимать решение. Последняя (в соответствии с гл. 2) характеризуется значением параметра , определяющего вели­чину потерь 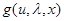при принятии решения u, и данными наблюде­ния х, на основе которых принимается решение в соответствии с пра­вилом u = u(x). Пусть теперь имеется N ситуаций, сходных или связан­ных с основной, в которых получены те или иные эмпирические данные. Каждая из них для характеризуется значением пара­метров , имеющих ту же природу, состав и содержание, что и параметры . Иными словами, если для ситуации, в которой принимается интересующее нас решени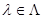е, , где 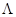- множество возможных зна­чений параметров , то и каждое из значений является одним из возможных элементов множества 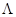; если имеет распределение с плотностью 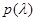, то и каждое из значений имеет то же распределение.

В общем случае эмпирические данные представляют собой совокуп­ность значений , каждая из составляющих этой совокупности соответствует значению и может содержать тот или иной объем сведений. Характер, значимость и способы использования этих све­дений существенно различаются в зависимости от того, производится ли в -й ситуации только наблюдение и регистрация каких-либо данных (аналогичных х для основной рабочей ситуации либо как-то отличаю­щихся от х) или наряду с наблюдением, так же как в рабочей ситуации, осуществляется принятие решения 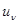с вытекающими отсюда последствиями. Согласно принятой терминологии, в первом случае гово­рят о простом обучении, а во втором - о «рабочеподобном». Смысл последнего термина связан с тем, что при получении эмпирических данных воспроизводится не только ситуация, характеризуемая значе­нием параметра , определяющим потери, но и сам процесс решения, подобный тому, который должен быть выполнен в рабочей ситуации. Это является принципиальной основой для получения информации о конкретной величине потерь от принятия решения на каждом -м ша­ге и использования этой информации для улучшения правила принятия решения на рабочем шаге.

Рассмотрим более полно возможный состав эмпирических дан­ных - совокупности 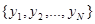для различных случаев. Заметим, что эта совокупность часто называется обучающей последовательностью.

Дата добавления: 2015-09-03